11. Bode Plot绘制与讲解

Bode Plot将系统的频率特性 G(j\omega) 用图示的方法表示出来。Bode Plot一大优点就是把整个频率特性的作图分解为传递函数的不同零极点和增益的幅频和相频曲线的简单叠加。我们知道一个传递函数中的零极点和增益决定了系统的响应形式，因此通过研究每个零极点和增益的幅相曲线，就可以理解每个环节在整体系统中作用。最后通过叠加把所有环节的曲线相加，就可以得到最后的Bode Plot。

使用MATLAB的Bode命令可以快速画出Bode Plot。不过手绘Bode的能力也是非常有用的，很多时候我们可以快速草绘一个近似图线来做出判断，并不需要借助计算机。单独环节的Bode Plot是十分重要的，这一篇我们主要讲讲几个非常常见的传递函数环节（term）的画法，重点是微分环节和积分环节。

本篇目录：

1. Bode Plot 原理

2. 三类重要环节

A. 比例积分微分

B. 惯性环节与一阶微分环节

C. 二阶振荡环节与二阶微分环节

3. 本篇小节

1.Bode Plot原理

一个开环传递函数如6.15所示，可以通过简单的变换写作6.16的形式。其中n是和系统type有关的数，显然0型系统n=0，I型系统n=-1等等。化成这种形式的好处在于帮助我们快速确定每个环节的转折频率（corner frequency），对于每个环节来说，也可以叫做该环节的截止频率（cutoff frequency）。但应当注意这和滤波器中的通常-3dB的截止频率定义还略有区别。

具体例子如6.17所示，这个开环传递函数表明这是个II型系统（Type II）。它有1个零点，和3个极点，一个开环增益。6.17实际上由4个虚数组成（我们将实数也视为虚部为0的虚数）。频率特性最后也是这个4个虚数相乘除的结果，同样也是个虚数，并且在极坐标（polar coordinate）下可以表示成幅值与相角的形式。根据复数的基础知识，虚数相除的结果为虚数，其模值为原虚数模值相除，相角相减。于是便有了式子6.18的相角计算公式。我们对6.17两边取模并取log，于是将模之间的乘除变成了对数之间的相减，有了6.19的幅值计算公式。注意到我们采用分贝dB为单位，那么对6.19两边乘以20并取10为底，则有了公式6.20。

至此根据6.18和6.20就可以在半对数坐标轴上画出Bode Plot了。作图过程应该是将每一个部分的幅频和相频曲线绘制出来，然后最后将4个部分的曲线相加。

2. 三类重要环节

我们分别说一下三类重要的环节的Bode Plot，也可以认为是零极点或者不同零极点的组合形式。

A. 比例K 纯积分1/s 纯微分s

看到这里我们很熟悉吧，是不是想起了PID？是的，这三个环节的频率特性都可以归类为 K{{s}^{n}}=K{{(j\omega )}^{n}} 。我们下面把三个经典的环节拆开来看。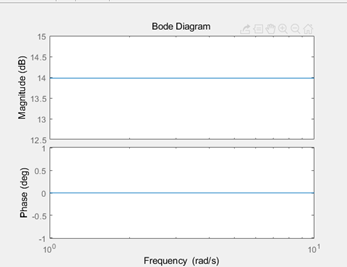

上图为比例环节K=5时的Bode Plot。

显然K=5时幅值是一个常数5，频率特性 G(j\omega)=5 的实部为5，虚部为0。因此幅值在纵轴上为 20{{\log }_{10}}(5)=\text{13}\text{.9794 dB} 约为14dB。相位由于虚部为0，则相角为0。对比上图，我们可以验证我们的分析是正确的。

很自然的，我们知道K的取值只会影响幅值的位置，即增大K会让曲线往上移动，反之往下移动。但是相位并没有任何影响。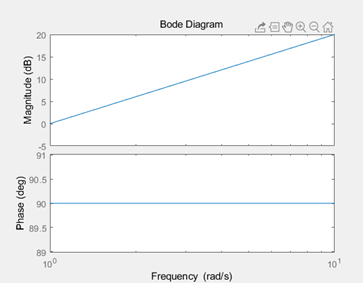

上图为纯微分环节 s=j\omega 的Bode Plot。

频率特性 G(j\omega)=j\omega 的实部为0，虚部为 \omega 。因此幅值在纵轴上为 20\log_{10}(\omega) ，在半对数坐标中斜率为20dB/decade。相位由于虚部位于虚轴的正半轴，则相角为90度（或顺时针计算为-270度）。对比上图，我们发现 20\log_{10}(1)=0 ,正如分析所言。

微分环节是不能独立存在，因此理想的微分器也不能物理实现。传递函数含有纯微分环节的系统是非因果的，简单地讲就是系统当前的输出受到未来输入的影响。现实中的系统必然是因果的。于是实际中的微分器是一种近似实现，我们在根轨迹的Lead Compensator设计那篇就讲过，它是对理想PD控制器的一种近似。经典的微分器可以写作：

G(s)=\frac{s}{Ts+1}\Rightarrow G(j\omega )=\frac{j\omega }{Tj\omega +1} \\

当T=0.5时的Bode Plot为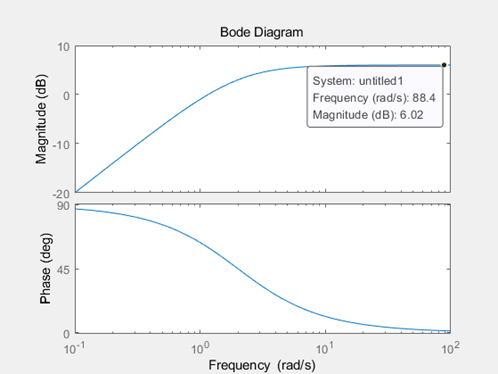

其中T为时间常数，如果T可以取得非常小，那么这个传递函数就会非常接近s。这其实就是一个高通滤波器HPF，其截止频率为6.02-3=3.02dB处的频率。对比纯微分环节和经典微分器的Bode Plot，我们发现在低频段他们的幅频和相频特性是相近的，但是达到cutoff frequency之后，微分器的输出幅值变化就不大明显了，维持在最后的常值。我们可以通过传递函数看出，当s很大时，幅值就是常数 20{{\log }_{10}}(1/T)

\[\underset{\omega \to \infty }{\mathop{\lim }}\,\left| G(j\omega ) \right|=\underset{\omega \to \infty }{\mathop{\lim }}\,\left| \frac{j\omega }{Tj\omega +1} \right|=\underset{\omega \to \infty }{\mathop{\lim }}\,\left| \frac{T{{\omega }^{2}}}{{{T}^{2}}{{\omega }^{2}}+1}+\frac{\omega j}{{{T}^{2}}{{\omega }^{2}}+1} \right|=\underset{\omega \to \infty }{\mathop{\lim }}\,\frac{\sqrt{{{T}^{2}}{{\omega }^{4}}-{{\omega }^{2}}}}{{{T}^{2}}{{\omega }^{2}}+1}\approx \underset{\omega \to \infty }{\mathop{\lim }}\,\frac{T{{\omega }^{2}}}{{{T}^{2}}{{\omega }^{2}}+1}=\frac{1}{T}\]

我们发现，这个经典微分器在高频部分的信号最终会被放大 20{{\log }_{10}}(1/T) 倍。为了让微分器有更好的近似效果，我们需要一个很小的T值，这样作为微分器的工作频段就能较大，更接近理想的纯微分环节，但是对于高频的信号小T值会导致一个很大增益。如果我们需要微分的信号中含有噪声，噪声的频率一般都是比较高的，或者是高低频段都有分布，过小的T会导致信号的噪音被放大数倍甚至数十倍，破坏信号的原信号的信噪比，导致输出信号被污染严重而不能使用。实际选择的T会控制在一个合适的数字，并且输入信号要通过低通滤波器把高频噪音预先过滤一遍，提高输出信号的品质。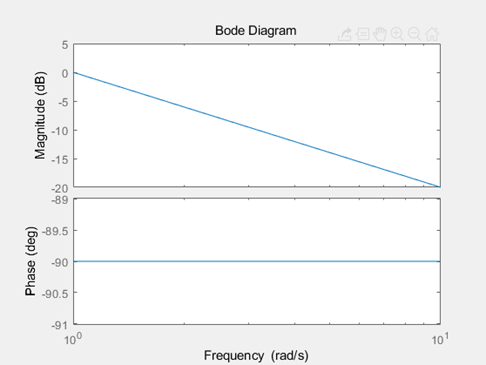

上图为纯积分环节 G(jw)=\frac{1}{jw} 的Bode Plot。

频率特性 G(j\omega )=\frac{1}{j\omega }=-\frac{j}{\omega } 的实部为0，虚部为 -\frac{1}{\omega} 。因此幅值在纵轴上为 20{{\log }_{10}}(\frac{1}{\omega })=-20{{\log }_{10}}(\omega ) 在半对数坐标中斜率为-20dB/decade。相位由于虚部位于虚轴的负半轴，则相角为-90度（或逆时针计算为270度）。对比上图，我们发现 20{{\log }_{10}}(10)=-20 ，正如分析所言。

纯积分环节是可以独立存在的，我们在电路中经常用到积分器。我们发现和纯微分环节相反，纯积分环节 G(s)=\frac{1}{s} 的幅频曲线是以-20dB/decade的速度下降的，相位也是正好反相。我们关注高频部分，其幅值是不断衰减的，意味着积分器可以有效的对高频信号进行抑制。我们在根轨迹部分讲到的的Lag Compensator，它是对PI控制器的一种近似。一个Lag Compensator可以是下面这样子的，z>p：

G(s)={{K}_{p}}+{{K}_{i}}\frac{1}{s+p}=\frac{{{K}_{p}}(s+p)+{{K}_{i}}}{s+p}=\frac{{{K}_{p}}s+{{K}_{p}}p+{{K}_{i}}}{s+p}={{K}_{p}}\frac{s+(p+\frac{{{K}_{i}}}{{{K}_{p}}})}{s+p}=K\frac{s+z}{s+p}

为了使得Lag Compensator很好的近似积分器的效果，显然p就应该尽量小。但我们之前也讲过，p不能过于小，因为这样会增加一个衰减很慢的模态，从而延长系统的调节时间。一个较小的p和一个合适的z，会让这个补偿器的DC gain变大，从而串联到开环系统中能够提高整个DG的开环传递函数的DC gain，这有利于闭环系统稳态误差的减小（如果你忘记了的话，就要回去翻翻之前的关于System Type的文章了。）

例如z=10，p=3，K=1时的Bode Plot为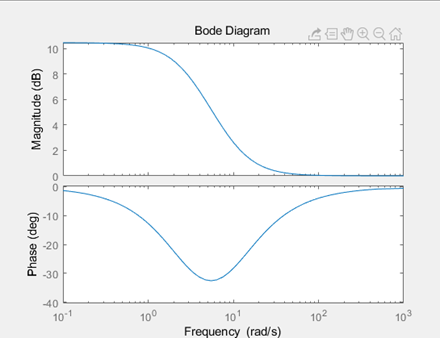

G(j\omega )=\frac{\frac{1}{10}j\omega +1}{\frac{1}{3}j\omega +1} \\

那么这个Compensator的DC gain约10.45dB，串联后可以将原开环系统的DC gain放大了3倍。高频部分的幅值为0dB，相位也接近0，意味着高频部分会保留原样通过（如果K不等于1，则高频部分会被放大或者缩小）。注意这和低通滤波器还不一样，我们稍后会讲到。观察频率1到10之间近似微分的相频曲线，当p的取值越来越小时，输出相位滞后也会越来越接近90度，即纯积分环节，这也就是为什么这称为滞后补偿器Lag Compensator了。 那至于超前补偿器Lead Compensator可以想象，当z>p，Bode Plot就是上下翻转的，低频段幅值低，高频段被放大或者缩小，相位得到了提前，随着p的增大，近似微分频段的相位提前越来越接近90度。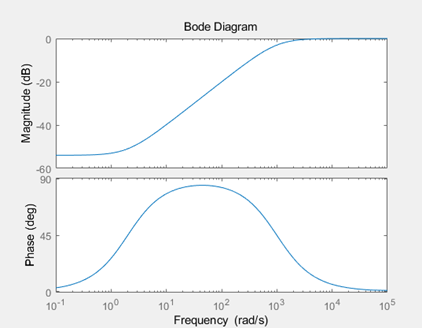

G(s)=\frac{s+2}{s+1000} \\

总结这个环节的特点：

K{{s}^{n}}=K{{(j\omega )}^{n}} 类环节根据n的不同，幅频曲线可能是常值（n=0），或是以n * 20dB/decade为斜率的直线(n>0 或者n

当 s=j\omega 较小时，其幅频和相频曲线与常值1的曲线是一样的，幅值为0dB，相位为0。在该微分环节的转折频率 \omega=\frac{1}{T}=1rad/s 后，其幅频与相频逐渐随着频率的增加与纯微分环节相似，幅值为 \[20{{\log }_{10}}(T\omega )\] ，因为 \underset{\omega \to 0}{\mathop{\lim }}\,G(j\omega )\approx Tj\omega =Ts

注意到绘制幅值曲线时，有两条渐近线，一条是频率很小时的 \[20{{\log }_{10}}(T\omega \text{+}1)\approx 20{{\log }_{10}}(1)=0\] dB线，还有一条是频率很大时的幅值曲线

\[20{{\log }_{10}}(T\omega \text{+}1)\approx 20{{\log }_{10}}(T\omega )\] 。当 \omega=\frac{1}{T} 时，取值为0dB，因此我们得到两条渐近线（Asymptotes）在0dB的 \omega=\frac{1}{T} 处相交。这个 \omega 就是一阶微分环节的转折频率。

相位的变化可以从频率特性中看出，频率很小时的相角与常数相角相近，为0度。随着频率增大，与理想微分环节的相角相同，为90度。当频率为转折频率 \omega=\frac{1}{T} 时，实部为1，虚部为j，则相位为45度。再取另外两个相位接近0和90度的频率，得到三条渐进线的位置，可以画出相频曲线。 以下是一个例子：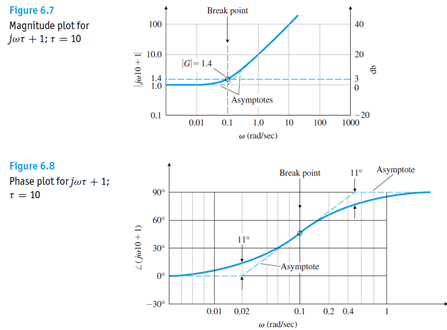

那么对于惯性环节 \frac{1}{Tj\omega+1} 来说，我们通过相似的分析就可知道，其低频和常数有类似的频率特性幅值为0dB，相角为0度，其高频幅频近似纯积分，应该以-20db/dec不断衰减， 相角接近90度。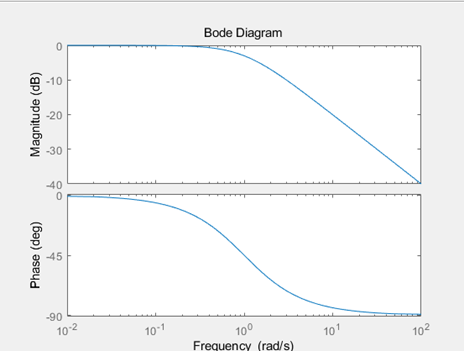

No surprise. 图已经告诉我们，我们的分析时完全正确的。以T=1为例，同样转折频率是1 rad/s。这时候的系统 G(s)=\frac{1}{Ts+1} 我们称为一阶惯性系统，T为时间常数，越大表明其惯性越大，并且其具有低通滤波器的性质。（仔细观察图谱，自己确认是不是低通滤波器把）。实际上只要是分母阶次大于分子的系统，都具有类似的Bode Plot。我们之前讲过实际绝大多数系统对于高频的响应都会慢慢衰减，他们都存在这种Low-pass filter的性质。时间常数越大，我们就会发现这个LPF的截止频率，或者我们叫Bandwidth带宽也越小。

我们知道一阶惯性系统的时域响应特点，如果时间常数很大，那么系统响应速度就会变慢，代表着系统的惯性也大。这和小带宽，低截止频率是统一的。典型的一阶系统就是RC电路，RC的乘积即为时间常数。我们知道如果电容越大，或者电阻越大，那么这个电容两端充满电的时间就会越长。这在大部分控制教材和本科电工学，模拟电路教材上都有讲过。如果忘记了，请回头再翻翻看。

C. 二阶振荡环节与二阶微分

二阶振荡和二阶微分，其频率特性为 G(j\omega )={{[{{(j\omega /{{\omega }_{n}})}^{2}}+2\zeta (j\omega /{{\omega }_{n}})+1]}^{\pm 1}} 其中前者为分数形式，后者为多项式。

关于这两个环节的曲线绘制，只要找到了幅频和相频的公式就基本没什么太大问题。这在[2]的“5-2典型环节与开环系统的频率特性处”有详细地推导。其基本思路也就只是把幅频和相频根据原频率特性写出，然后让幅频函数对频率 \omega 求导，得到共振峰处的谐振频率为 {{\omega }_{r}}={{\omega }_{n}}\sqrt{1-{{\zeta }^{2}}} ，注意这两个函数都代表了有阻尼的系统，因此发生共振时的频率并不是刚好在自然频率 \omega_n 处。当 \zeta 比较小时，自然频率与谐振频率之间是十分接近的（如 \zeta=0.2 , \omega_r=0.9798\omega_n ）。下图为二阶振荡环节的Bode Plot。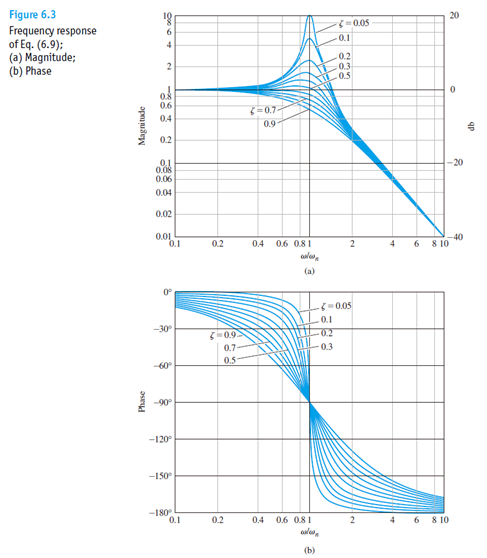

分析频率特性为 G(j\omega )={{[{{(j\omega /{{\omega }_{n}})}^{2}}+2\zeta (j\omega /{{\omega }_{n}})+1]}^{\pm 1}} 。当频率较小时，其与常值1相近，所以开始的幅频为0dB，相位也近于0度。当频率比较大时，二次项会主导整个式子，于是其幅值便为\[20{{\log }_{10}}\left| G(j\omega ) \right|\approx 20{{\log }_{10}}\left| {{[{{(j\omega /{{\omega }_{n}})}^{2}}]}^{\pm 1}} \right|=\pm 40{{\log }_{10}}\left| \omega /{{\omega }_{n}} \right|\] 。由此得到高频时的渐近线为通过 \omega=\omega_n 斜率为 \pm40 dB/decade的直线。注意到高频时二次项主导后， s^2 与 \frac{1}{s^2} 的频率特性相近，所以相位也会最终趋于 \pm180 度。在发生共振时，我们从幅频中看出实部为0，虚部在虚轴正半轴或者负半轴，此时相角为 \pm90 度。而在共振峰附近频率的过渡过程就与阻尼的大小有关了。从上图中我们可以看出，阻尼越小，共振峰的峰值越大。通过对幅频曲线公式进行求导可以得到具体地峰值。振荡环节的峰向上突，微分环节的峰向下突。这也很容易理解，因为微分环节的二次多项式取到最小值，而振荡环节是其倒数，自然取到的是最大值了。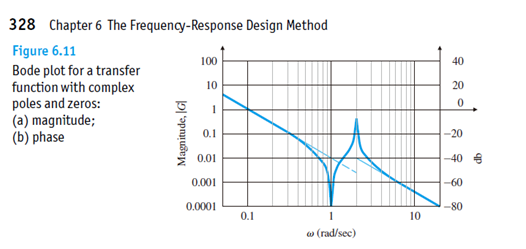

最后提一句，这个Bode Plot在机械振动研究单自由度二阶系统时一定会出现，相信学机械的同学一定不会陌生。经典二阶系统的例子就是： Mass-Spring-Damper System（振子-弹簧-阻尼系统）。共振时相位差为-90度也是必须要知道的常识。

3. 本篇小节

Bode Plot是非常重要的频域分析工具，可以将一个系统的频域特性图示。频域特性作为系统在频域中的模型，在Bode Plot中可以被分解成多个不同环节单独绘制并叠加。Bode Plot帮助我们更好地理解了微分环节，积分环节以及信号处理的一些概念。

Reference：

[1] G.F. Franklin, J.D. Powell, A.Emami-Naeini, Feedback Control of Dynamic Systems, 7th Edition, 2014, Pearson

[2] 胡寿松，自动控制原理（第六版），2013，科学出版社