【数学】凸函数与詹森不等式（琴生不等式）解析

2023-11-25 00:13| 来源: 网络整理| 查看: 265

【数学】凸函数与詹森不等式（琴生不等式）

文章目录【数学】凸函数与詹森不等式（琴生不等式）0. 介绍1 凸函数和凹函数2 琴生不等式（詹森不等式）

0. 介绍

詹森不等式、琴生不等式（Jensen Inequality）是以丹麦技术大学数学家约翰·延森（Johan Jensen）命名的，给出积分的凸函数值和凸函数的积分值间的关系的数学名词。

琴生（Jensen）不等式（也称为詹森不等式），使用时注意前提、等号成立条件。

凸函数是数学函数的一类特征。凸函数就是一个定义在某个向量空间的凸子集C（区间）上的实值函数。凸函数是一个定义在某个向量空间的凸子集C（区间）上的实值函数f，而且对于凸子集C中任意两个向量, f((x1+x2)/2)>=(f(x1)+f(x2))/2，则f(x)是定义在凸子集c中的凸函数（该定义与凸规划中凸函数的定义是一致的，下凸）。

理解：

闭区间上存在一系数小于1的正数，它们的和等于1。在闭区间[a,b]上的凸函数f(x)上取与这些小于1的正数同样多个自变量，分别用这些小于1的正数乘以各个自变量，一一对应，并求它们的和的函数值；另一方面用这些小于1的正数，分别乘以各个自变量的函数，保持与前者相同的一一对应关系，再求这些函数值的和。那么和的函数值与函数值的和有如下的关系。当f上凸时，和的函数值不小于函数值的和；当f下凸时，和的函数值不大于函数值的和。特别的，当这些小于1的正数的个数为2时，就形成了凸函数的定义。 1 凸函数和凹函数下凸函数（凸函数），从几何意义上看，下凸函数就是任意两点之间的弦（即这两点构成的线段）都在该函数图像（此处是指这两点之间的函数图像，而非全部的函数图像）的上方。在这里插入图片描述

上凸函数（也即，凹函数），从几何意义上看，上凸函数就是任意两点之间的弦（即这两点构成的线段）都在该函数图像（此处是指这两点之间的函数图像，而非全部的函数图像）的下方。在这里插入图片描述

2 琴生不等式（詹森不等式）

琴生不等式以丹麦技术大学数学家约翰·延森（John Jensen）命名。它给出积分的凸函数值和凸函数的积分值间的关系。琴生（Jensen）不等式（也称为詹森不等式），使用时注意前提、等号成立条件。

对于凸函数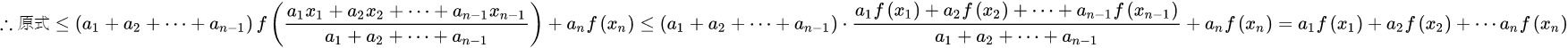：在这里插入图片描述

证明：

对于凹函数（上凸函数），变号即可。

【本文地址】

公司简介

联系我们