|
python 无人机、飞机轨迹(含姿态角)可视化方法
5月前
作者:木子泽月生 分类:Toy博客
阅读(44)
违法举报
这篇具有很好参考价值的文章主要介绍了python 无人机、飞机轨迹(含姿态角)可视化方法。希望对大家有所帮助。如果存在错误或未考虑完全的地方,请大家不吝赐教,您也可以点击"举报违法"按钮提交疑问。
无人机、飞机轨迹(含姿态角)可视化方法
目标:在三维直角坐标系中画出包含无人机位置pos、偏航角yaw、俯仰角pitch、滚转角roll等姿态的飞行轨迹。
思路:同时建立机体坐标系和直角坐标系,飞机的所有点在机体坐标系中的坐标是不变的,而通过俯仰角pitch、偏航角yaw以及滚转角pitch就可以完成从机体坐标系到直角坐标系的转换。因此,在可视化飞行轨迹时,只需要把pos作为机体坐标系的原点,然后根据三个角度进行转换(旋转)即可。
1.原始飞机图像点位
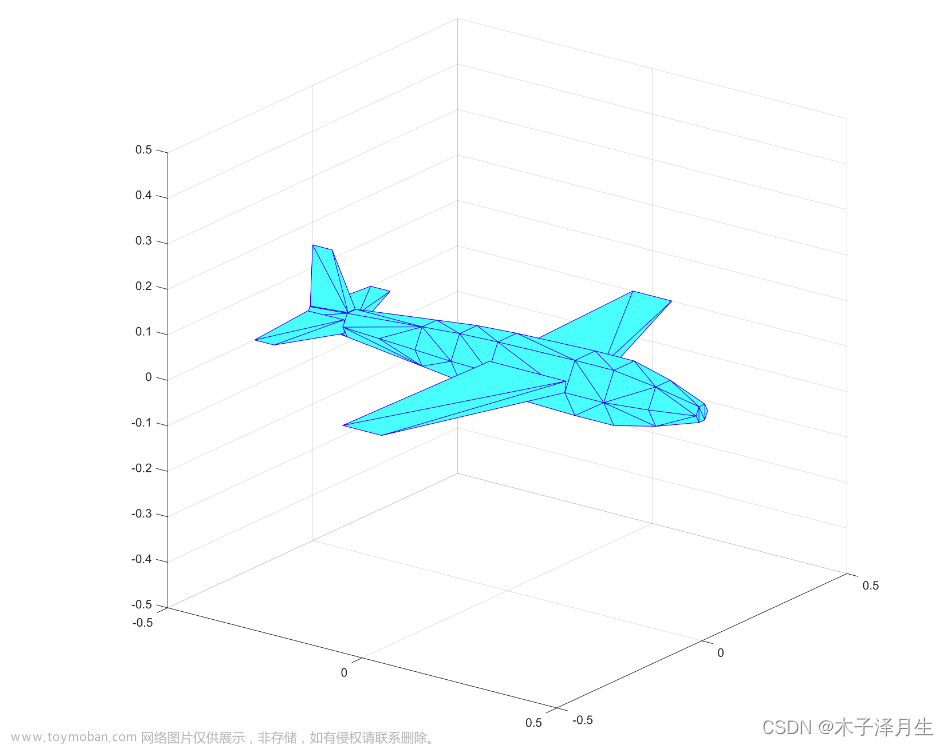 (以下为生成该飞机的matlab代码) (以下为生成该飞机的matlab代码)
%% 148*3 三角连接矩阵
TR=[1 50 41;1 51 50;2 51 1;3 51 2;3 53 51;3 43 53;3 4 43;4 3 52;5 4 52;5 47 4;5 49 47;6 49 5;6 54 49;7 54 6;8 54 7;9 54 8;9 16 54;9 10 16;10 9 28;11 10 28;11 14 10;11 13 14;12 13 11;13 12 24;13 24 14;14 24 20;15 14 20;15 10 14;16 10 15;15 48 16;17 48 15;17 37 48;17 36 37;18 36 17;18 8 36;19 8 18;9 8 19;9 19 28;19 55 28;19 35 55;19 18 35;18 20 35;18 17 20;17 15 20;20 24 35;21 35 24;22 35 21;22 34 35;22 28 34;22 29 28;22 23 29;23 22 21;23 21 56;21 33 56;21 24 33;24 25 33;12 25 24;25 12 11;25 11 26;26 32 25;26 27 32;27 26 30;26 29 30;11 29 26;28 29 11;29 23 30;30 23 56;27 30 56;31 27 56;32 27 31;33 32 31;25 32 33;33 31 56;34 28 55;35 34 55;36 8 7;36 7 38;37 36 38;38 46 37;38 39 46;39 38 7;40 39 7;39 40 1;1 45 39;1 41 45;41 42 45;42 41 43;43 4 42;42 4 44;42 44 45;44 47 45;4 47 44;45 47 46;45 46 39;46 47 37;37 47 48;47 49 48;48 49 16;49 54 16;41 50 43;50 53 43;51 53 50;1 40 2;2 40 3;3 40 52;52 40 7;6 52 7;6 5 52;57 60 59;57 58 60;58 57 61;57 62 61;57 59 62;59 58 62;60 58 59;61 62 58;63 64 66;64 63 68;64 68 67;65 64 67;66 64 65;63 66 65;63 65 67;67 68 63;69 71 73;70 71 69;71 70 74;70 73 74;70 69 73;72 74 73;72 71 74;71 72 73;75 76 79;76 75 77;77 75 80;75 79 80;78 80 79;78 76 80;76 78 79;76 77 80;81 82 85;82 81 83;83 81 86;81 85 86;84 86 85;84 82 86;82 84 85;82 83 86];
%% 86*3 三维坐标矩阵(表示86个点在三维空间中的坐标)
X=[[0.4 0.025 -0.0433012701892219;0.4 0.05 0;0.4 0.025 0.0433012701892219;0.4 -0.025 0.0433012701892219;0.3 -0.035 0.0606217782649107;0.2 0.035 0.0606217782649107;0.2 0.07 0;0 0.065 0;-0.1 0.03 0.0519615242270663;-0.1 -0.03 0.0519615242270663;-0.2 -0.025 0.0433012701892219;-0.3 -0.04 0;-0.2 -0.05 0;-0.1 -0.06 0;0 -0.065 0;0 -0.0325 0.0562916512459885;0 -0.0325 -0.0562916512459885;-0.1 0.03 -0.0519615242270663;-0.1 0.06 0;-0.1 -0.03 -0.0519615242270663;-0.4 0.015 -0.0259807621135332;-0.4 0.03 0;-0.5 0.02 0;-0.2 -0.025 -0.0433012701892219;-0.4 -0.03 0;-0.4 -0.015 0.0259807621135332;-0.5 -0.01 0.0173205080756888;-0.2 0.025 0.0433012701892219;-0.4 0.015 0.0259807621135332;-0.5 0.01 0.0173205080756888;-0.5 -0.01 -0.0173205080756888;-0.5 -0.02 0;-0.4 -0.015 -0.0259807621135332;-0.3 0.04 0;-0.2 0.025 -0.0433012701892219;0 0.0325 -0.0562916512459885;0.2 -0.035 -0.0606217782649107;0.2 0.035 -0.0606217782649107;0.3 0.035 -0.0606217782649107;0.3 0.07 0;0.5 -0.01 -0.0173205080756888;0.5 -0.02 0;0.5 -0.01 0.0173205080756888;0.4 -0.05 0;0.4 -0.025 -0.0433012701892219;0.3 -0.035 -0.0606217782649107;0.3 -0.07 0;0.2 -0.07 0;0.2 -0.035 0.0606217782649107;0.5 0.01 -0.0173205080756888;0.5 0.02 0;0.3 0.035 0.0606217782649107;0.5 0.01 0.0173205080756888;0 0.0325 0.0562916512459885;-0.2 0.05 0;-0.5 0.01 -0.0173205080756888;0.2 0.0657784834550136 0.0239414100327968;0 0.0562916512459885 -0.0325;0.05 0.5 0;0.2 0.07 -0;0 0.061080020351084 0.0222313093161685;-0.05 0.5 0;0 -0.0562916512459885 -0.0325;0.2 -0.0657784834550136 0.0239414100327968;0.05 -0.5 0;0.2 -0.07 -0;-0.05 -0.5 0;0 -0.061080020351084 0.0222313093161685;-0.45 0.2 0;-0.4 0.0259807621135332 0.015;-0.4 0.0259807621135332 -0.015;-0.5 0.0173205080756888 -0.01;-0.5 0.2 0;-0.5 0.0173205080756888 0.01;-0.4 -0.0259807621135332 0.015;-0.4 -0.0259807621135332 -0.015;-0.45 -0.2 0;-0.5 -0.0173205080756888 -0.01;-0.5 -0.0173205080756888 0.01;-0.5 -0.2 0;-0.4 0.012678547852221 0.0271892336110995;-0.4 -0.012678547852221 0.0271892336110995;-0.45 0 0.15;-0.5 -0.00845236523481399 0.018126155740733;-0.5 0.00845236523481399 0.018126155740733;-0.5 0 0.15]];
%% 绘制三角曲面
trisurf(TR, X(:,2),X(:,1),X(:,3), 'FaceColor','cyan','edgecolor','blue');
axis equal;
axis([-0.5 0.5 -0.5 0.5 -0.5 0.5]);
2.建立机体坐标系
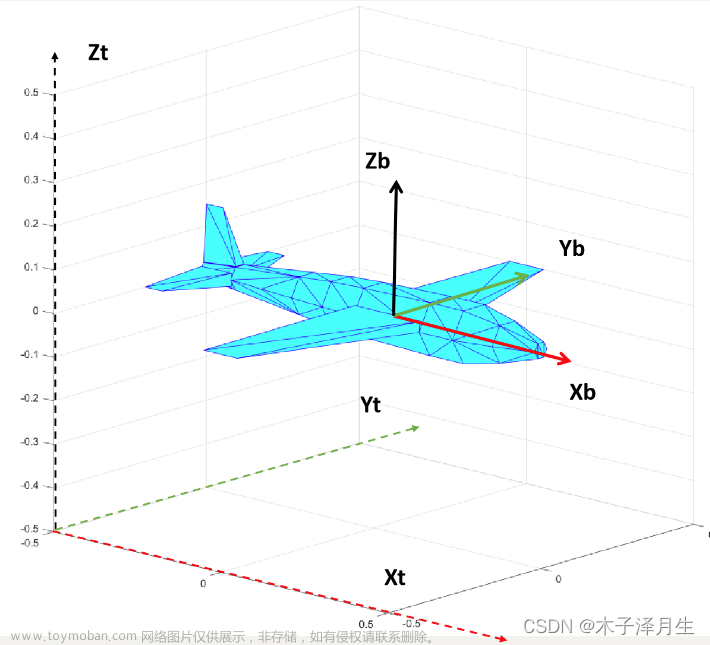 上述机体坐标系的原点为飞机质心,
x
b
x_b
xb轴平行于机身轴线,指向机头;
y
b
y_b
yb轴垂直于飞机纵向对称面,指向右侧机翼;
z
b
z_b
zb轴垂直于
x
b
x_b
xb轴和
y
b
y_b
yb轴构成的屏幕,指向座舱上方;三个坐标轴的方向满足右手螺旋定则。 上述机体坐标系的原点为飞机质心,
x
b
x_b
xb轴平行于机身轴线,指向机头;
y
b
y_b
yb轴垂直于飞机纵向对称面,指向右侧机翼;
z
b
z_b
zb轴垂直于
x
b
x_b
xb轴和
y
b
y_b
yb轴构成的屏幕,指向座舱上方;三个坐标轴的方向满足右手螺旋定则。
下面看飞机的质心在直角坐标系中的坐标
(
O
x
t
,
O
y
t
,
O
z
t
)
(Ox_t,Oy_t,Oz_t)
(Oxt,Oyt,Ozt):
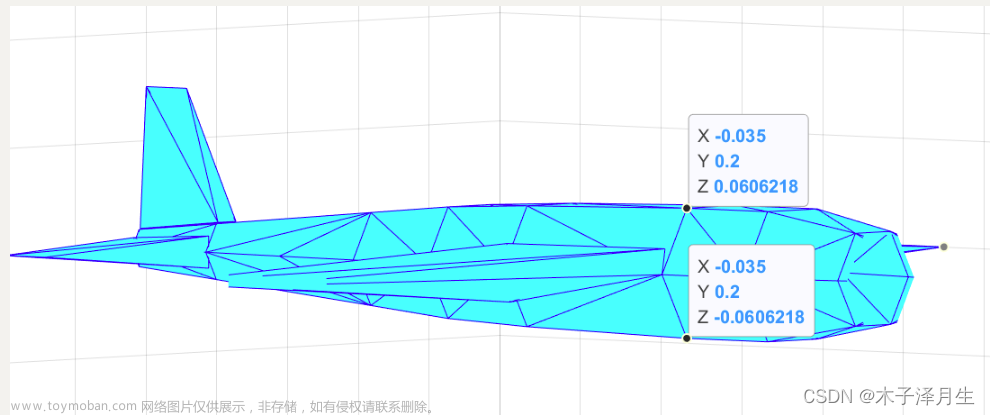 上图表明:
O
z
t
=
0
Oz_t=0
Ozt=0 上图表明:
O
z
t
=
0
Oz_t=0
Ozt=0

上图表明:
O
x
t
=
0
Ox_t=0
Oxt=0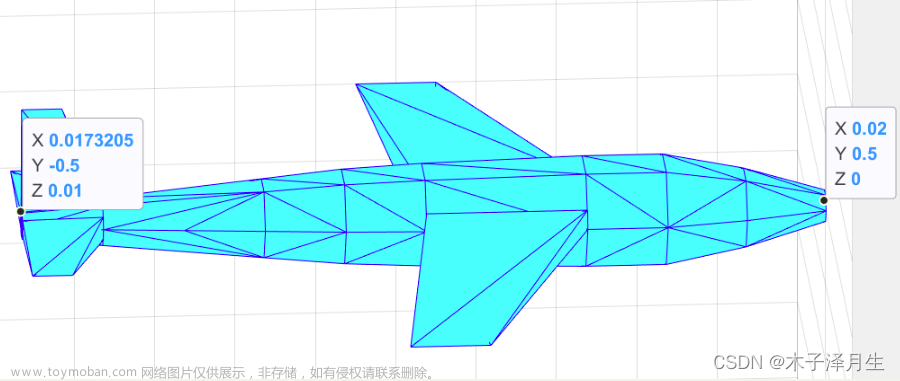 上图表明:
O
y
t
=
0
Oy_t=0
Oyt=0 由此可知,在当前状态下,直角坐标系(0,0,0)与机体坐标系(质心)的原点是一致的,并且在上面的图中可以看出各个坐标轴的方向也一致,因此当前飞机在直角坐标系中的坐标恰可以作为其在该机体坐标系的坐标。 上图表明:
O
y
t
=
0
Oy_t=0
Oyt=0 由此可知,在当前状态下,直角坐标系(0,0,0)与机体坐标系(质心)的原点是一致的,并且在上面的图中可以看出各个坐标轴的方向也一致,因此当前飞机在直角坐标系中的坐标恰可以作为其在该机体坐标系的坐标。
PS:而飞机在机体坐标系中的坐标不会发生变化,因此只需要将质心移动到pos处,再根据三个角度进行旋转,即可在直角坐标系中画出包含Pos、俯仰角、偏航角以及滚转角的飞行轨迹。
3.坐标系转换
假设得到一组飞行参数(pos,pitch,yaw,roll),用以下步骤完成飞机的可视化:
根据旋转矩阵对原来的机体坐标系坐标进行旋转(旋转方向为z,y,x) 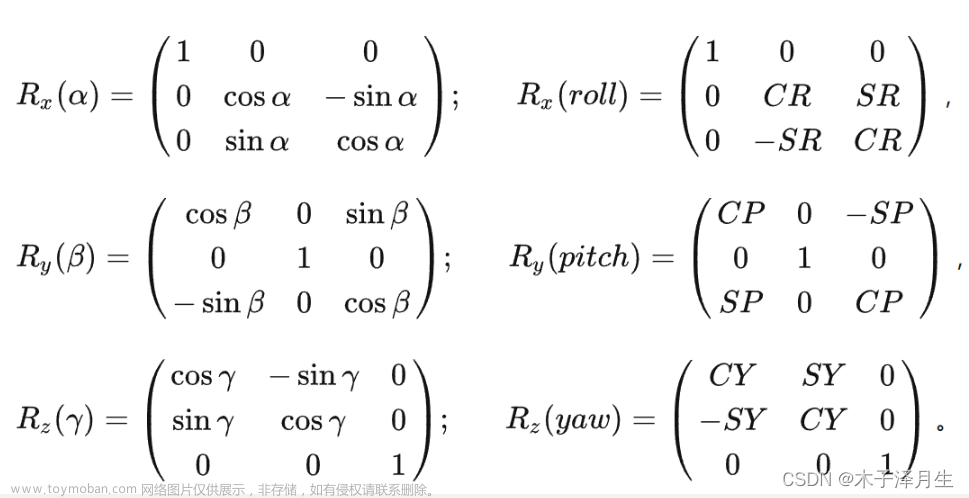 
以上矩阵为由直角坐标系到机体坐标系的转换矩阵,记作
R
t
2
b
R_{t2b}
Rt2b;另外设无人机在机体坐标系和直角坐标系的坐标分别为
I
b
I_b
Ib和
I
t
I_t
It,故有:(旋转要左乘)
I
b
=
R
t
2
b
I
t
I_b=R_{t2b}I_t
Ib=Rt2bIt 故有:
I
t
=
R
t
2
b
−
1
I
b
I_t=R_{t2b}^{-1}I_b
It=Rt2b−1Ib 最后再将整个无人机平移Pos向量,即可得到可以表示无人机位姿的直角坐标:
I
t
=
R
t
2
b
−
1
I
b
+
P
o
s
I_t=R_{t2b}^{-1}I_b+Pos
It=Rt2b−1Ib+Pos
4.代码实现效果(matlba)
pos=[500,1000,500];pitch=pi/6;yaw=pi/6;roll=pi/2;
Draw3DTraj(pos,pitch,yaw,roll);
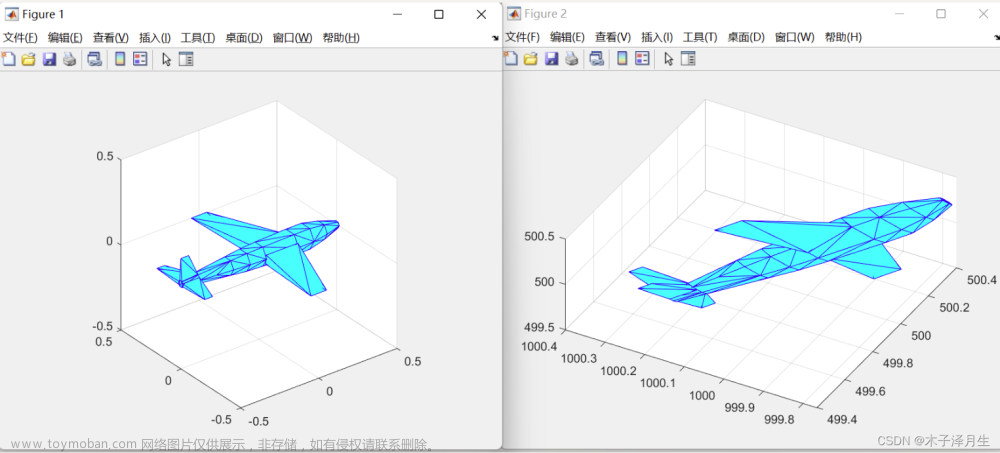
5.飞行轨迹效果(改为python实现)文章来源:https://www.toymoban.com/news/detail-424850.html
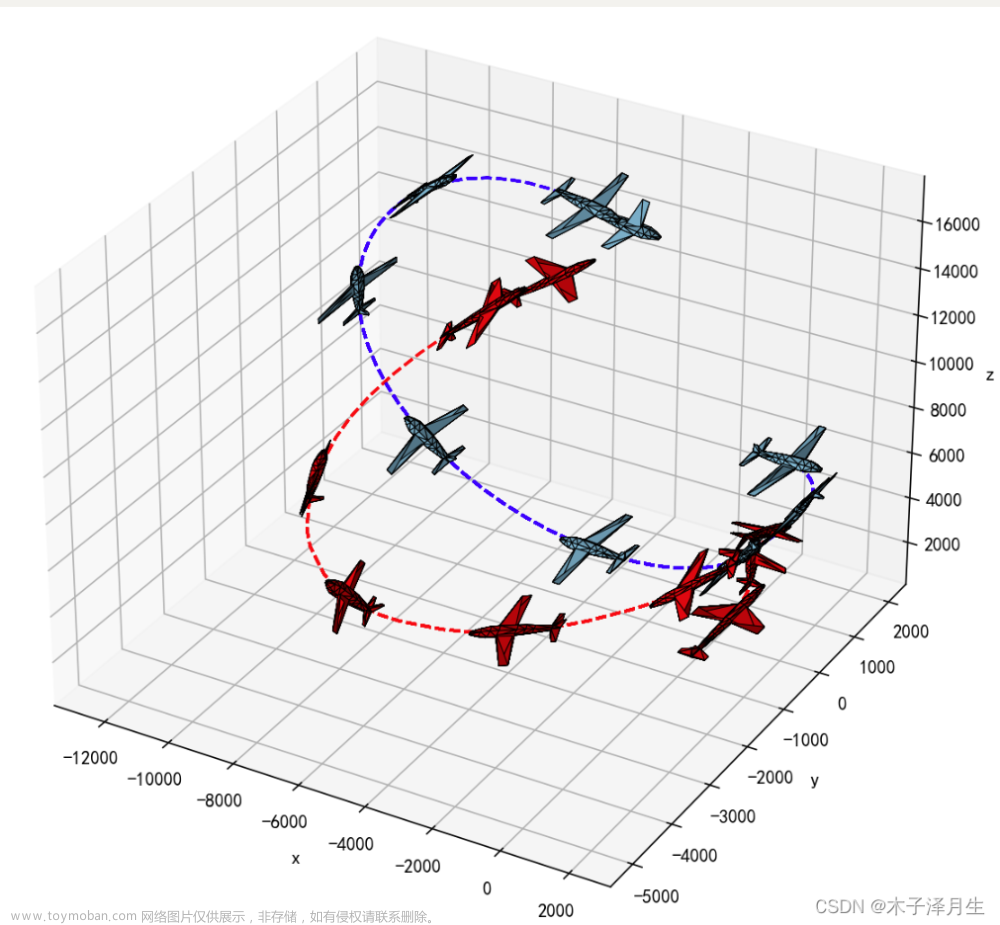 文章来源地址https://www.toymoban.com/news/detail-424850.html 文章来源地址https://www.toymoban.com/news/detail-424850.html
到了这里,关于python 无人机、飞机轨迹(含姿态角)可视化方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处: 如若内容造成侵权/违法违规/事实不符,请点击违法举报进行投诉反馈,一经查实,立即删除!
分享到:
领支付宝红包
赞助服务器费用
|  (以下为生成该飞机的matlab代码)
(以下为生成该飞机的matlab代码) 上述机体坐标系的原点为飞机质心,
x
b
x_b
xb轴平行于机身轴线,指向机头;
y
b
y_b
yb轴垂直于飞机纵向对称面,指向右侧机翼;
z
b
z_b
zb轴垂直于
x
b
x_b
xb轴和
y
b
y_b
yb轴构成的屏幕,指向座舱上方;三个坐标轴的方向满足右手螺旋定则。
上述机体坐标系的原点为飞机质心,
x
b
x_b
xb轴平行于机身轴线,指向机头;
y
b
y_b
yb轴垂直于飞机纵向对称面,指向右侧机翼;
z
b
z_b
zb轴垂直于
x
b
x_b
xb轴和
y
b
y_b
yb轴构成的屏幕,指向座舱上方;三个坐标轴的方向满足右手螺旋定则。 上图表明:
O
z
t
=
0
Oz_t=0
Ozt=0
上图表明:
O
z
t
=
0
Oz_t=0
Ozt=0
 上图表明:
O
y
t
=
0
Oy_t=0
Oyt=0 由此可知,在当前状态下,直角坐标系(0,0,0)与机体坐标系(质心)的原点是一致的,并且在上面的图中可以看出各个坐标轴的方向也一致,因此当前飞机在直角坐标系中的坐标恰可以作为其在该机体坐标系的坐标。
上图表明:
O
y
t
=
0
Oy_t=0
Oyt=0 由此可知,在当前状态下,直角坐标系(0,0,0)与机体坐标系(质心)的原点是一致的,并且在上面的图中可以看出各个坐标轴的方向也一致,因此当前飞机在直角坐标系中的坐标恰可以作为其在该机体坐标系的坐标。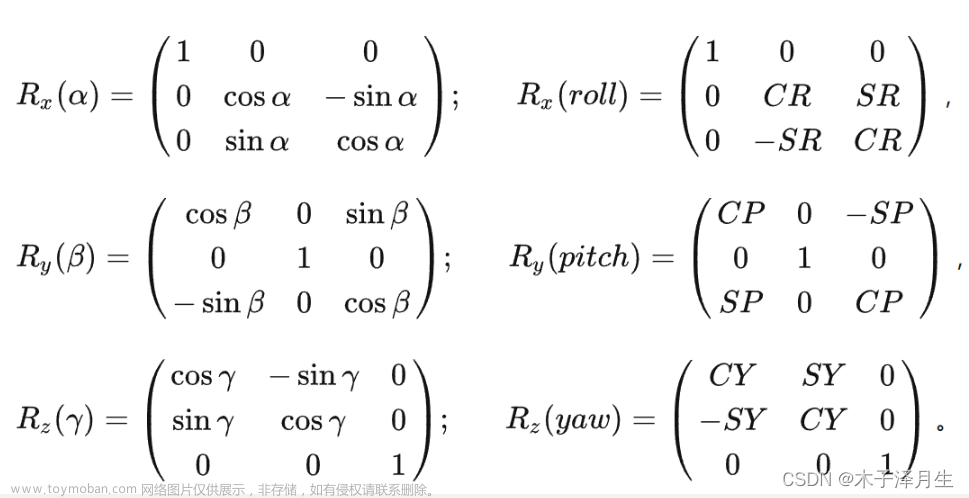


 文章来源地址https://www.toymoban.com/news/detail-424850.html
文章来源地址https://www.toymoban.com/news/detail-424850.html