| 从时频特性出发 | 您所在的位置:网站首页 › 循环位移序列图解 › 从时频特性出发 |
从时频特性出发
|
目录
背景知识——离散傅里叶级数(DFS)和离散傅里叶变换(DFT)线性卷积和循环卷积从时域看从频域看
联想——OFDM中加CP的解释结论
背景知识——离散傅里叶级数(DFS)和离散傅里叶变换(DFT)
首先回顾一套定理性质的规律: 时域 连续非周期 信号对应频域 非周期连续 信号 时域 连续周期 信号对应频域 非周期离散 信号 时域 离散非周期 信号对应频域 周期连续 信号 时域 离散周期 信号对应频域 周期离散 信号 这四对儿都不拆不散的鸳鸯,在这儿咱们关注第四句 时域离散周期信号对应频域周期离散信号 翻译翻译,就是说,时域周期性导致频域离散化,时域离散化将导致频域的周期延拓,从频域导回时域也一样。再定眼一看,这个对应关系是四组中唯一的“离散”对“离散”的。一看见离散就开始上劲了。 数据离散化对应的操作是抽样,我们看看抽这一对鸳鸯的画面。
公式是这么回事儿: x ~ ( n ) = 1 N ∑ k = 0 N − 1 X ~ ( k ) e j 2 π N n k \tilde x(n) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {\tilde X(k){e^{j\frac{{2\pi }}{N}nk}}} x~(n)=N1k=0∑N−1X~(k)ejN2πnk X ~ ( k ) = ∑ n = 0 N − 1 x ~ ( n ) e − j 2 π N n k \tilde X(k) = \sum\limits_{n = 0}^{N - 1} {\tilde x(n){e^{ - j\frac{{2\pi }}{N}nk}}} X~(k)=n=0∑N−1x~(n)e−jN2πnk 上面这东西,就叫傅里叶级数(DFS)。一般编matlab的更喜欢下面的矩阵形式 X ~ = F N x ~ x ~ = 1 N F N ∗ X ~ \begin{array}{l} \tilde X = \mathop F\nolimits_N \tilde x\\ \tilde x = \frac{1}{N}\mathop F\nolimits_N^* \tilde X \end{array} X~=FNx~x~=N1FN∗X~ F N ∈ N × N \mathop F_N \in N×N FN∈N×N是matlab里用来执行fft的矩阵, F N ( k , n ) = e − j 2 π N k n \mathop F_N(k,n)={{e^{ - j\frac{{2\pi }}{N}kn}}} FN(k,n)=e−jN2πkn 数据上写‘~’就是为了标记这种周期性的数据,在后续的推导中,看见’~'就知道是长的周期序列。另外注意,这个求和区间是在0到N-1一个周期内,不是 − ∞ -\infty −∞到 + ∞ +\infty +∞。 以上就是DFS的基本方案。至于防混叠的抽样间隔选取,z域表达,DFS各种特性等,跟这篇文章关系不大,不说。 回过头来,常识知道随便给我一个信号,它不可能自带周期性,DFS就玩不转。需要做改变,这个骚操作就叫周期延拓,给一个不是无限长的信号,能让它戴上’~'周期化。翻过来看,从周期序列变到一段实值函数,就是加窗操作。 x ( n ) = x ~ ( n ) R N ( n ) x(n) = \tilde x(n){R_N}(n) x(n)=x~(n)RN(n) 对这个不带浪的 x ( n ) x(n) x(n)的时频变换操作,就是DFT。相应的操作就变成了下面的 x ( n ) = 1 N ∑ k = 0 N − 1 X ( k ) e j 2 π N n k \ x(n) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {X(k){e^{j\frac{{2\pi }}{N}nk}}} x(n)=N1k=0∑N−1X(k)ejN2πnk X ( k ) = ∑ n = 0 N − 1 x ( n ) e − j 2 π N n k \ X(k) = \sum\limits_{n = 0}^{N - 1} {x(n){e^{ - j\frac{{2\pi }}{N}nk}}} X(k)=n=0∑N−1x(n)e−jN2πnk 这么一看DFS与DFT没啥大区别,非也。一个是对无限长具有周期性函数的展开,一个是对任一有限长函数的操作,这是实现了不可为到为之的向前一小步。 线性卷积和循环卷积 从时域看咱们这一块倒着推,先从承认它的存在开始。后续从频域看时,咱们再从它们开始往后推。 怼公式。 y ( n ) = x ( n ) ∗ h ( n ) = ∑ m = − ∞ ∞ x ( m ) h ( n − m ) y(n) = x(n)*h(n) = \sum\limits_{m = - \infty }^\infty {x(m)h(n - m)} y(n)=x(n)∗h(n)=m=−∞∑∞x(m)h(n−m) 这是线性卷积,它有一个基本特性是长度M和长度N的两个序列卷一块,出来的是M+N-1的一个序列。 再怼公式。 x 3 ( n ) = x 1 ( n ) ⊗ x 2 ( n ) = [ ∑ m = 0 N − 1 x ~ 1 ( m ) x ~ 2 ( n − m ) ] R N ( n ) \begin{array}{l} {x_3}(n) = {x_1}(n) \otimes {x_2}(n)\\ \;\;\;\;\;\;\;\; = \left[ {\sum\limits_{m = 0}^{N - 1} {{{\tilde x}_1}(m){{\tilde x}_2}(n - m)} } \right]{R_N}(n) \end{array} x3(n)=x1(n)⊗x2(n)=[m=0∑N−1x~1(m)x~2(n−m)]RN(n) 这是循环卷积,开始有点蒙了。再说,它是两个长度一样的序列卷一块,出来的还是长度为N的序列,还会循环移位了。更蒙了,啥啥啥啊。咱们一点点看。 一个字,线性卷积周期延拓为周期卷积,周期卷积取主值区间为循环卷积。 意思是搞懂周期卷积就行了呗。 y ~ ( n ) = x ~ 1 ( n ) ∗ x ~ 2 ( n ) = ∑ m = 0 L − 1 x ~ 1 ( m ) x ~ 2 ( n − m ) = ∑ m = 0 L − 1 x ~ 2 ( m ) x ~ 1 ( n − m ) \begin{array}{c} \tilde y(n) = {{\tilde x}_1}(n)*{{\tilde x}_2}(n)\\= \sum\limits_{m = 0}^{L - 1} {{{\tilde x}_1}(m){{\tilde x}_2}(n - m)} \\= \sum\limits_{m = 0}^{L - 1} {{{\tilde x}_2}(m){{\tilde x}_1}(n - m)} \end{array} y~(n)=x~1(n)∗x~2(n)=m=0∑L−1x~1(m)x~2(n−m)=m=0∑L−1x~2(m)x~1(n−m) 这就叫周期卷积,是两个周期相同的均为L序列,在一个周期内的卷积结果。那么,上面公式里n-m是怎么实现的,也即序列周期卷积时是怎么移位的呢? 一张图。 从图里看,有限序列的循环移位包括3步。 1.周期延拓 2.移位 3.加窗 ( ( ⋅ ) ) N ((·))_N ((⋅))N表示模除N。从一个周期看,上述效果就是循环移位了。然后同一个周期内的两个序列对应相乘再求和,周期卷积结果就出来了。 跟线性卷积不一样的是,“一个周期内” 进行卷积就把它的长度拿捏得死死的了。再长,没用,卡住。完事儿再加个窗,循环卷积结果就出来了,这是从时域来看。 发现端倪了,上面说的线性卷积的长度M+N-1和周期卷积的L啥关系。一个字,没关系。他们只不过是两种运算规则定义的自身属性,能有啥关系。不过要是从数值结果来看,也能扯上点渊源。如果想让长为L的一个周期内的循环卷积的结果,是纯的,不跟旁边周期掺和的,就得满足L>M+N-1。那循环卷积在操作时,两个序列长度分别是M和N,又咋变成L的,补零就成了。阅尽千帆,卷积还是那个卷积,是套路复杂了。 从频域看怼公式。 地球人都知道,对一般的线性卷积来说,时域卷积对应频域乘积。 y ~ ( n ) = x 1 ( n ) ∗ x 2 ( n ) ↔ Y ~ ( k ) = X ~ 1 ( k ) ⋅ X ~ 2 ( k ) \tilde y(n) = {x_1}(n)*{x_2}(n) \leftrightarrow \tilde Y(k) = {{\tilde X}_1}(k) \cdot {{\tilde X}_2}(k) y~(n)=x1(n)∗x2(n)↔Y~(k)=X~1(k)⋅X~2(k) 敲黑板,这是有限求和还是无限求和?无限。 无限的玩不了,咱就想办法把有限的玩好。经过循环卷积,时域已经完成了有限操作,那么,它对应的频域形式是什么? 先给结论,与时域循环卷积对应的,是频域DFT的乘积。注意嗷,这两类操作都是有限的。 再怼公式。 老套路,给了两个频域有限信号 X 1 ( k ) 和 X 2 ( k ) X_1(k) 和 X_2(k) X1(k)和X2(k) ,先延拓为 X 1 ( ( k ) ) N 和 X 2 ( ( k ) ) N X_1((k))_ N 和 X_2((k)) _N X1((k))N和X2((k))N。 令 Y ( k ) = X 1 ( k ) ⋅ X 2 ( k ) Y(k) = {X_1}(k) \cdot {X_2}(k) Y(k)=X1(k)⋅X2(k), 则 Y ( ( k ) ) N = X 1 ( ( k ) ) N ⋅ X 2 ( ( k ) ) N Y{((k))_N} = {X_1}{((k))_N} \cdot {X_2}{((k))_N} Y((k))N=X1((k))N⋅X2((k))N 对 Y ( ( k ) ) N Y{((k))_N} Y((k))N做IDFS运算 y ( ( n ) ) N = 1 N ∑ k = 0 N − 1 Y ( ( k ) ) N F − k n = 1 N ∑ k = 0 N − 1 [ ∑ m = 0 N − 1 x 1 ( ( m ) ) N F k m ] [ ∑ r = 0 N − 1 x 2 ( ( r ) ) N F k r ] F − k n = ∑ m = 0 N − 1 x 1 ( ( m ) ) N ∑ r = 0 N − 1 x 2 ( ( r ) ) N [ 1 N ∑ k = 0 N − 1 F − k ( n − m − r ) ] \begin{array}{c} y{((n))_N} = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {Y{{((k))}_N}{F^{ - kn}}} \\ = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {\left[ {\sum\limits_{m = 0}^{N - 1} {{x_1}{{((m))}_N}{F^{km}}} } \right]\left[ {\sum\limits_{r = 0}^{N - 1} {{x_2}{{((r))}_N}{F^{kr}}} } \right]{F^{ - kn}}} \\ = \sum\limits_{m = 0}^{N - 1} {{x_1}{{((m))}_N}} \sum\limits_{r = 0}^{N - 1} {{x_2}{{((r))}_N}} \left[ {\frac{1}{N}\sum\limits_{k = 0}^{N - 1} {{F^{ - k(n - m - r)}}} } \right] \end{array} y((n))N=N1k=0∑N−1Y((k))NF−kn=N1k=0∑N−1[m=0∑N−1x1((m))NFkm][r=0∑N−1x2((r))NFkr]F−kn=m=0∑N−1x1((m))Nr=0∑N−1x2((r))N[N1k=0∑N−1F−k(n−m−r)] 最后一个中括号里是有正交性的,其结果只有当 r = n + m r=n+m r=n+m的时候才为 1 1 1,别的时候都是0,上面这个式子就可以化成 y ( ( n ) ) N = ∑ m = 0 N − 1 x 1 ( ( m ) ) N x 2 ( ( n − m ) ) N y({(n))_N}= \sum\limits_{m = 0}^{N - 1} {{x_1}({{(m)})_N}} {x_2}({(n - m))_N} y((n))N=m=0∑N−1x1((m))Nx2((n−m))N 这不就是周期卷积么,再加个窗,就得到下面的式子,也就是循环卷积了。 y ( n ) = y ( ( n ) N ) R N ( n ) = x 1 ( n ) ⊗ x 2 ( n ) y(n) = y({(n)_N}){R_N}(n) = {x_1}(n) \otimes {x_2}(n) y(n)=y((n)N)RN(n)=x1(n)⊗x2(n) 另外,由于时频域的对偶性,可以推测有限的时域乘积对应的是有限的频域卷积,也会有别的有趣的结论。不说了。 联想——OFDM中加CP的解释这也是我对循环卷积产生困惑的点。 现在想来,从时域上看,宽带信道的多径效应和带限特性会产生ISI,用数据片段末端数据作为cyclic pilot (cp)后,把不同径的数据段 “补齐” ,可以统一 “裁剪” 的同时还不损失原本数据,就克服了ISI。 从频域上看呢?因为是对有限数据进行的时频变换,循环卷积一直存在。假设多径产生的信道冲激响应长度为M,数据段长度为N,一个周期内会产生的卷积的长度为M+N-1。而如果不加CP,接收端以N为窗去截断,就会丢失数据。如果加上CP,使得L=N+CP≥M-N-1,即CP大于等于信道冲激响应强度,循环卷积这时就以L为窗去截了,截到的结果就是线性卷积的循环移位。为此,频域上数据没有丢失,变成了有限长度信道冲激响应和有限长度数据的频域的乘积。所以ISI在频域上也被消除了。 结论最后给结论,玩有限的时候,时域循环卷积对应的是频域DFT乘积。玩无限的时候,时域线性卷积对应的是频域DTFT乘积。 情况就是这么个情况,因为本科不是搞通信的,这问题困扰了我好久,从认知的角度来说进行了一次不系统的推理,希望对大家有所帮助。第一次编辑,不太会套路,可能会有赘述,谢谢大家包涵。 |
【本文地址】
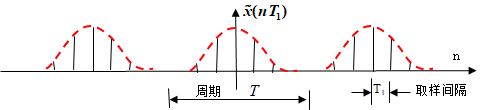 图1:信号的时域表示(抽样后)
图1:信号的时域表示(抽样后)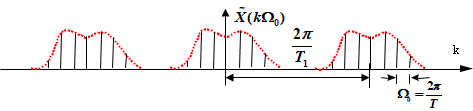 图2:信号的时域表示(抽样后)
图2:信号的时域表示(抽样后) 图3:有限序列的循环移位过程
图3:有限序列的循环移位过程