理论力学笔记（六）：碰撞与散射

动量与能量守恒会给出力学过程的很多性质，而且这些性质不依赖与具体的相互作用细节。

我们先讨论一个粒子在无外力的作用下分裂成两个粒子的过程。在与分裂前粒子的静止参考系中观察是容易的。

0→1+20 \rightarrow 1 + 2 0→1+2

分裂前后动量守恒：

0=p1+p20 = \bm{p}_1 + \bm{p}_2 0=p1​+p2​

能量守恒：

E0=E1+p122m1+E2+p222m2E_0 = E_1 + \frac{p_1^2}{2m_1} + E_2 + \frac{p_2^2}{2m_2} E0​=E1​+2m1​p12​​+E2​+2m2​p22​​

注意上式中 EiE_iEi​ 表示的是粒子的“内能”，并不包括粒子运动的动能。由此在粒子分裂的过程中，初始粒子的内能转化为了分裂后粒子的动能，我们定义分裂能[1]^{[1]}[1]：

ε=E0−E1−E2=p122m1+p222m2\varepsilon = E_0 - E_1 - E_2 = \frac{p_1^2}{2m_1} + \frac{p_2^2}{2m_2} ε=E0​−E1​−E2​=2m1​p12​​+2m2​p22​​

我们之前谈到，对于两体问题，可以把动能分为相对动能与质心动能：

Ek=12Mvc2+12μu2E_k = \frac{1}{2}Mv_c^2 + \frac{1}{2}\mu u^2 Ek​=21​Mvc2​+21​μu2

于是，在粒子分裂过程中，分裂能全部转化为相对动能。

下图展示的是 m1=m2m_1 = m_2m1​=m2​ 时的分裂情况，对于 m1≠m2m_1 \neq m_2m1​​=m2​ 的一般情况，也好想象。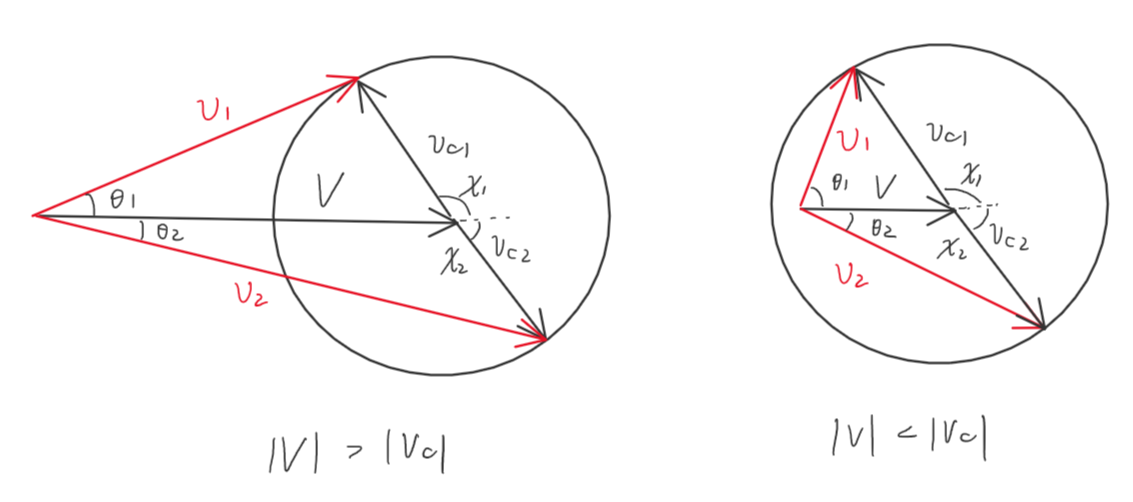

一般的，我们令粒子1在质心系中的速度为 vc1\bm{v}_{c1}vc1​，与 V\bm{V}V 的夹角为 χ1\chi_1χ1​:

若无特别说明，χ\chiχ 均指在质心系中的散射角；θ\thetaθ 指在实验系中的散射角。

v1=V+vc1\bm{v} _ 1 = \bm{V} + \bm{v} _ {c1} v1​=V+vc1​

容易得到：

{v1cos⁡θ1=V+vc1cos⁡χ1v1sin⁡θ1=vc1sin⁡χ1\left\{ \begin{aligned} & v_1 \cos\theta_1 = V + v_{c1}\cos\chi_1\\ & v_1 \sin\theta_1 = v_{c1}\sin\chi_1 \end{aligned} \right. {​v1​cosθ1​=V+vc1​cosχ1​v1​sinθ1​=vc1​sinχ1​​

进而有：

{v12=V2+vc12+2Vvc1cos⁡χ1tan⁡θ=vc1V+vc1cos⁡χ1\left\{ \begin{aligned} & v_1^2 = V^2 + v_{c1}^2 + 2Vv_{c1}\cos\chi_1\\ &\tan\theta = \frac{v_{c1}}{V + v_{c1}\cos\chi_1} \end{aligned} \right. ⎩⎨⎧​​v12​=V2+vc12​+2Vvc1​cosχ1​tanθ=V+vc1​cosχ1​vc1​​​

在物理学中经常遇到多个相同粒子分裂的情况，此时粒子分裂的出射角度是随机的。在质心系中观察粒子分裂得到的结果是很显然的：分裂的粒子将会以等同概率的向任意立体角出射。对于讨论实验系中的粒子分裂问题，此时母粒子以速度 VVV 运动。尽管在质心系中粒子仍然对任何立体角以等同概率出射，但此时在实验系中所观察到的粒子的角分布会改变。

例如，以上在质心系中观察到的应当是均匀分布（以下省略下标1）：

P(χ)=dΩ4π=12sin⁡χdχP(\chi) = \frac{d\Omega}{4\pi}=\frac{1}{2}\sin\chi d\chi P(χ)=4πdΩ​=21​sinχdχ

对应到实验系中，利用上述方程组，可得：

−2Vvcsin⁡χdχ=dv2=2mdT-2Vv_{c} \sin\chi d\chi = dv^2 = \frac{2}{m}dT −2Vvc​sinχdχ=dv2=m2​dT

改变 dTdTdT 符号，使得 dT>0dT > 0dT>0，有： 可得：

P(T)=dT2mvcVP(T) = \frac{dT}{2mv_cV} P(T)=2mvc​VdT​

对应的物理含义为：在实验系中观察到的粒子对动能均匀分布。

角度分布也容易得到：

dθcos⁡2θ=vc2sin⁡χ(V+vccos⁡χ)2dχ=tan⁡2θsin⁡χdχ\frac{d\theta}{\cos^2\theta}=\frac{v_{c}^2\sin\chi}{(V+v_c\cos\chi)^2}d\chi = \tan^2\theta \sin\chi d\chi cos2θdθ​=(V+vc​cosχ)2vc2​sinχ​dχ=tan2θsinχdχ

即：dθ=sin⁡2θsin⁡χdχd\theta = \sin^2\theta\sin\chi d\chidθ=sin2θsinχdχ

由此：

P(θ)=12sin⁡θdθ=12sin⁡χdχsin⁡3θ=vc3v3P(χ)\begin{aligned} P(\theta) &= \frac{1}{2}\sin\theta d\theta\\ &= \frac{1}{2}\sin\chi d\chi \sin^3\theta\\ &= \frac{v_c^3}{v^3} P(\chi) \end{aligned} P(θ)​=21​sinθdθ=21​sinχdχsin3θ=v3vc3​​P(χ)​

碰撞 是粒子在短时间内发生相互作用然后改变运动状态的过程。在碰撞的过程中，由于动量守恒，质心动能守恒，但是相对动能可能会损失，转化为其他形式的能量（注意，此处的损失是针对初态和末态而言的）。若相对动能损失了，则称为 非弹性碰撞；若相对动能完全损失，则称为 完全非弹性碰撞；若相对动能未损失，则称为 弹性碰撞。对于两体碰撞而言，可以用恢复系数 eee 来表征碰撞的弹性。

注意，我们一般只对于宏观物体，谈论弹性和非弹性。宏观物体发生碰撞，相对动能常常转化为内能耗散掉，恢复系数 eee 只与碰撞的材料有关。

恢复系数定义为碰前后两体的相对速度之比：

e=ufuie = \frac{u_\mathrm{f}}{u_{\mathrm{i}}} e=ui​uf​​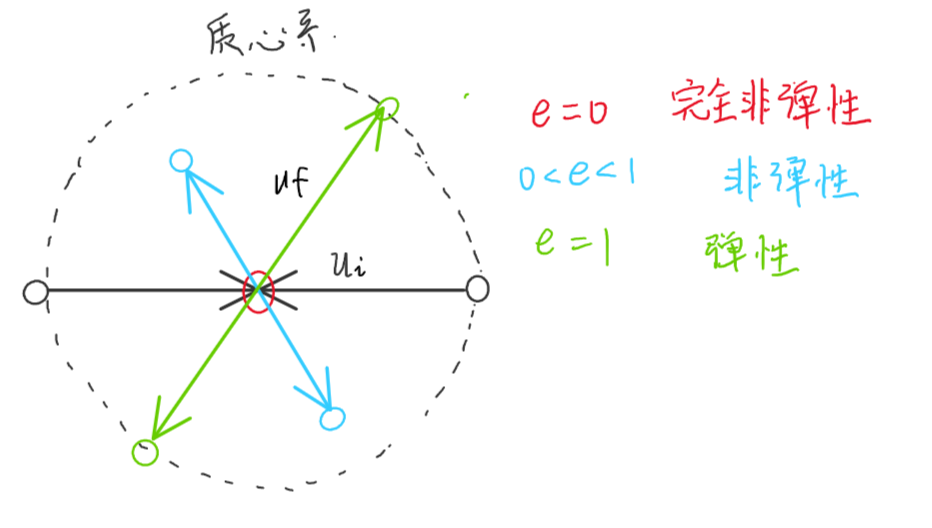

对于完全非弹性碰撞来说，如果从末态往初态看（从一个整体变成两个粒子），就是一个分裂过程。并且，完全非弹性碰撞由于知道末态只有整体运动，进行分析是很容易的。

启发式的，对于碰撞过程来说，我们可以假设存在一个中间态，此态中的相对动能为零（只有整体运动）。那么任何一个碰撞问题，都可以看作从中间态分别到初态、末态的分裂问题。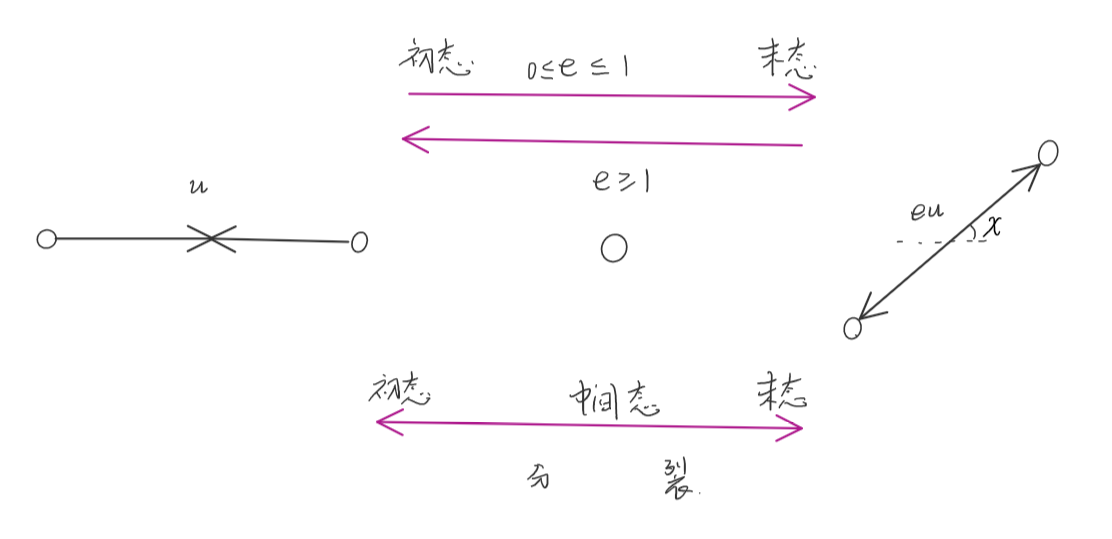

对于弹性碰撞的求解，使用恢复系数方程（碰撞前后相对速度不变）去代替能量守恒方程会简化问题的求解。

更一般的，若考虑碰撞的物体的形状，恢复系数可定义为碰撞点在碰撞前后的相对速度的比值。此时的碰撞情况更为复杂，但利用动量守恒，角动量守恒，能量守恒（或恢复系数方程），是可以解决问题的。若知道碰撞面的性质，例如碰撞面是光滑的，此时可以得到碰撞的冲量必定沿法向，此时能够完全把末态确定下来。

在粒子碰撞中，我们只是通过一些守恒律对可能的末态进行了讨论。如果我们知道相互作用的细节（散射势），就能够确定散射角。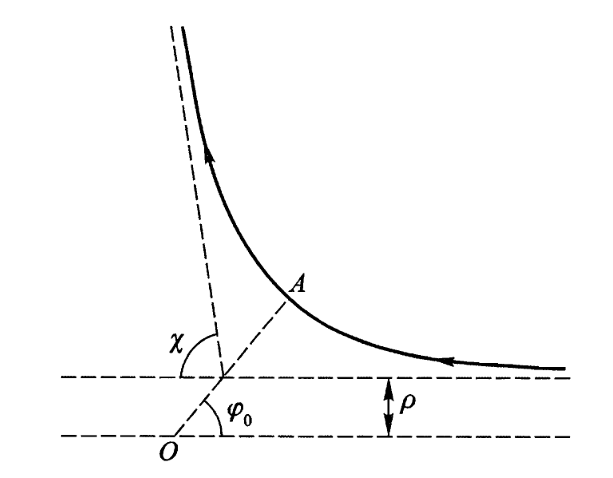

Fig: 粒子散射 [1]^{[1]}[1]

不失一般性的，我们考虑一个质量为 mmm 的粒子在中心势 U(r)U(r)U(r) 的散射情况。我们假设粒子从无穷远处入射，经过中心势散射后运动往无穷远处。假设粒子运动最近到 AAA 点，此时到 OOO 距离为 rminr_{min}rmin​，rminr_{min}rmin​。不难得到，粒子运动轨迹应当关于 OAOAOA 是对称的。入射轨道的渐近线与散射势中心 OOO 的距离为 瞄准距离，记作 r∞r_{\infty}r∞​。粒子散射过程中转过的角度 χ\chiχ 称为 散射角。

对于两体问题，可以将 mmm 认为是约化质量，以下的讨论仍然适用。

若该势能具有性质：lim⁡r→∞=0\lim_{r\rightarrow\infty} = 0limr→∞​=0，可以在无穷远处很方便的表示散射过程中的一些守恒量：

E=12mv∞2,L=mρv∞E = \frac{1}{2}mv_{\infty}^2,\quad L = \frac{m}\rho v_{\infty} E=21​mv∞2​,L=ρm​v∞​

根据上一篇笔记对中心势的讨论，我们可以把散射角写为：

χ=2∫rmin∞(L/r2)dr2m(E−U(r))−L2/r2=2∫rmin∞(ρ/r2)dr1−ρ2/r2−2U/mv∞2\begin{aligned} \chi &= 2\int_{r_{min}}^{\infty} \frac{(L/r^2) dr}{\sqrt{2m(E-U(r))-L^2/r^2}} \\ & = 2\int_{r_{min}}^{\infty}\frac{(\rho/r^2)dr}{\sqrt{1-\rho^2/r^2-2U/mv^2_{\infty}}}\\ \end{aligned} χ​=2∫rmin​∞​2m(E−U(r))−L2/r2​(L/r2)dr​=2∫rmin​∞​1−ρ2/r2−2U/mv∞2​​(ρ/r2)dr​​

由此只要给定 ρ\rhoρ，v∞v_{\infty}v∞​，U(r)U(r)U(r)。我们可以根据守恒律得到 rminr_{min}rmin​。散射角也就可以通过上式确定。

在大多数时候，我们并不关心一组特定参数下的散射角，我们往往关心一簇入射粒子的散射角的分布情况。简单地，我们考虑在无穷远处，有一簇速度为 v∞v_{\infty}v∞​ 的全同粒子束（我们假设这个粒子束在横截面上是均匀分布的）。

我们假定 χ\chiχ 与 ρ\rhoρ 是一一对应的，那么瞄准距离 ρ\rhoρ 相同的粒子，散射角度也相同。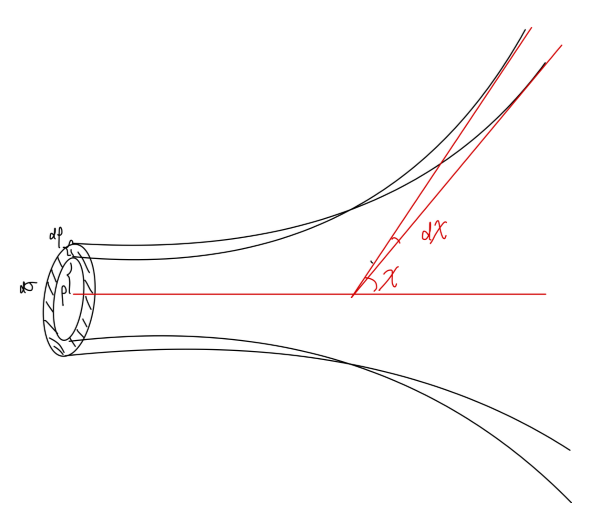

可以得到，散射角为 χ∼χ+dχ\chi\sim\chi+d\chiχ∼χ+dχ 内的粒子数就等同于瞄准距离在 ρ∼ρ+dρ\rho\sim \rho + d\rhoρ∼ρ+dρ 的粒子数，这将正比与面积 dσd\sigmadσ。

dn(χ)=dn(ρ)∼dσ=2πρdρdn(\chi) = dn(\rho) \sim d\sigma = 2\pi \rho d\rho dn(χ)=dn(ρ)∼dσ=2πρdρ

我们称 dσd\sigmadσ 为 有效截面：

dσ=2πρ∣dρ(χ)dχ∣dχd\sigma = 2\pi \rho |\frac{d\rho(\chi)}{d\chi}| d\chi dσ=2πρ∣dχdρ(χ)​∣dχ

其除以散射的立体角 dΩd\OmegadΩ，得到 微分散射截面：

dσdΩ=2πρ∣dρ(χ)dχ∣dχ2πsin⁡χdχ=ρsin⁡χ∣dρ(χ)dχ∣\frac{d\sigma}{d\Omega} = \frac{2\pi \rho |\frac{d\rho(\chi)}{d\chi}| d\chi}{2\pi \sin\chi d\chi} = \frac{\rho}{\sin\chi}|\frac{d\rho(\chi)}{d\chi}| dΩdσ​=2πsinχdχ2πρ∣dχdρ(χ)​∣dχ​=sinχρ​∣dχdρ(χ)​∣

对所有可能角度的散射进行积分，得到 总散射截面：

σt=∫0π2πρ∣dρ(χ)dχ∣dχ\sigma_t = \int_{0}^{\pi} 2\pi \rho |\frac{d\rho(\chi)}{d\chi}| d\chi σt​=∫0π​2πρ∣dχdρ(χ)​∣dχ

散射截面是一个很重要的物理量，特别是在粒子物理领域中。

我们现在对卢瑟福散射应用得到的散射截面公式。卢瑟福散射是指带电粒子在库伦场中的散射。

设散射势为：

U=arU = \frac{a}{r} U=ra​

其中 a>0a>0a>0 对应排斥势，a