| 两轮自平衡小车的LQR控制设计(1): 系统建模和LQR控制器设计 | 您所在的位置:网站首页 › 平衡小车算法有哪些种类 › 两轮自平衡小车的LQR控制设计(1): 系统建模和LQR控制器设计 |
两轮自平衡小车的LQR控制设计(1): 系统建模和LQR控制器设计
|
1.引言和实现效果
两轮自平衡小车是常见的轮式移动机器人,如果假设它的车身和车轮都为刚体且不受外界干扰,忽略摩擦,轮子与地面运动满足纯滚动条件,则可以简化为一个具有双轮的倒立摆系统,如下图所示。 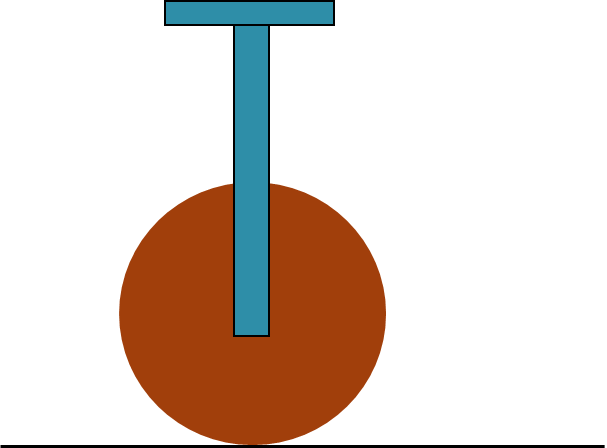
本文首先根据牛顿第二定律推导平衡小车的动力学模型,然后建立线性二次型最优控制器(LQR),实现平衡小车的自平衡控制,效果如下: 平衡小车系统建模参考:Ooi R C . Balancing a Two-Wheeled Autonomous Robot[J]. university of western australia, 2003. 2.1 直流电机模型设直流电机的电阻为 R R R,电感为 L L L,简化模型如下: 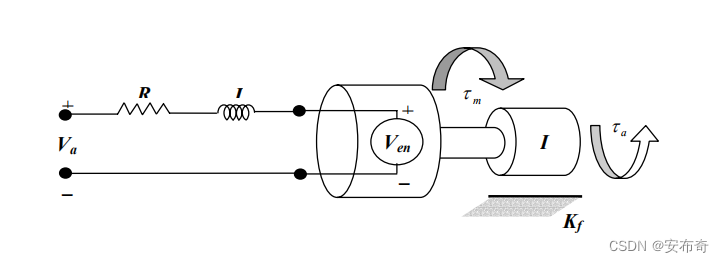
电机产生的总扭矩(不是输出扭矩)可以简化表示为电流的线性函数,即 τ m = k m i (2.1) \tau_m=k_mi\tag{2.1} τm=kmi(2.1) k m k_m km为电机的力矩常数。电机的感应电动势可以简化为转速的线性函数,即 V e n = k e w (2.2) V_{en}=k_ew\tag{2.2} Ven=kew(2.2) k e k_e ke为电机的感应电动势常数。根据基尔霍夫电压定律有 V a − R i − k e w − L d i d t = 0 (2.3) V_a-Ri-k_ew-L\frac{di}{dt}=0\tag{2.3} Va−Ri−kew−Ldtdi=0(2.3) 因为平衡小车的直流电机电感很小,可以近似为0,则有 i = V a R − k e w R (2.4) i=\frac{V_a}{R}-\frac{k_ew}{R}\tag{2.4} i=RVa−Rkew(2.4) 设感应电动势产生的反扭矩简化为 τ e \tau_e τe,电机轴上的附加扭矩为 τ a \tau_a τa,阻尼力矩 τ f = k f w \tau_f=k_fw τf=kfw为转速的线性函数,设电机轴的转动惯量为 I R I_R IR,则根据牛顿第二定律为 ∑ M = τ m − τ f − τ e − τ a = I R d w d t (2.5) \sum{M}=\tau_m-\tau_f-\tau_e-\tau_a=I_R\frac{dw}{dt}\tag{2.5} ∑M=τm−τf−τe−τa=IRdtdw(2.5) 由于直流电机的阻尼力矩 τ f \tau_f τf和反电动势产生的扭矩 τ e \tau_e τe很小,故可以忽略,则有 d w d t = k m I R i − τ a I R (2.6) \frac{dw}{dt}=\frac{k_m}{I_R}i-\frac{\tau_a}{I_R}\tag{2.6} dtdw=IRkmi−IRτa(2.6) 带入电流得到 d w d t = − k m k e I R R w + 1 I R R V a − τ a I R (2.7) \frac{dw}{dt}=-\frac{k_mk_e}{I_RR}w+\frac{1}{I_RR}V_a-\frac{\tau_a}{I_R}\tag{2.7} dtdw=−IRRkmkew+IRR1Va−IRτa(2.7) 2.2 两轮动力学模型选取左右车轮为研究对象,进行受力分析。 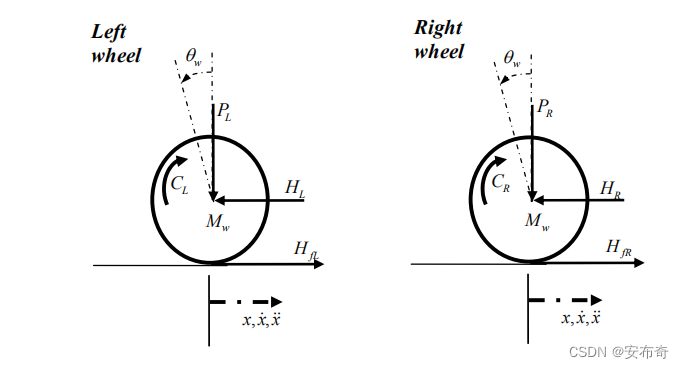
以右轮为例,根据牛顿第二定律有: (1)水平 x x x方向受力: M w x ¨ = H f R − H R (2.8) M_w\ddot{x}=H_{fR}-H_R\tag{2.8} Mwx¨=HfR−HR(2.8) 其中 M w M_w Mw为车轮质量, x ¨ \ddot{x} x¨为车轮质心运动加速度, H R H_R HR为车架对车轮的反作用力, H f R H_{fR} HfR为地面摩擦力。 (2)绕质心转动力矩: I w θ ¨ w = C R − H f R r (2.9) I_w\ddot{\theta}_w=C_R-H_{fR}r\tag{2.9} Iwθ¨w=CR−HfRr(2.9) 其中 I w I_w Iw为车轮转动惯量, θ w \theta_w θw为车轮转动角度, r r r为车轮半径, C R C_R CR为电机对轮的驱动力矩,即 C R = I R d w d t = − k m k e R θ ˙ w + k m R V a (2.10) C_R=I_R\frac{dw}{dt}=\frac{-k_mk_e}{R}\dot{\theta}_w+\frac{k_m}{R}V_a \tag{2.10} CR=IRdtdw=R−kmkeθ˙w+RkmVa(2.10) 则有 I w θ ¨ w = − k m k e R θ ˙ w + k m R V a − H f R r (2.11) I_w\ddot{\theta}_w=\frac{-k_mk_e}{R}\dot{\theta}_w+\frac{k_m}{R}V_a-H_{fR}r\tag{2.11} Iwθ¨w=R−kmkeθ˙w+RkmVa−HfRr(2.11) 因此 H f R = − k m k e R r θ ˙ w + k m R r V a − I w r θ ¨ w (2.12) H_{fR}=\frac{-k_mk_e}{Rr}\dot{\theta}_w+\frac{k_m}{Rr}V_a-\frac{I_w}{r}\ddot{\theta}_w\tag{2.12} HfR=Rr−kmkeθ˙w+RrkmVa−rIwθ¨w(2.12) 带入水平方向受力方程得到对于左轮有: M w x ¨ = − k m k e R r θ ˙ w + k m R r V a − I w r θ ¨ w − H L (2.13) M_w\ddot{x}=\frac{-k_mk_e}{Rr}\dot{\theta}_w+\frac{k_m}{Rr}V_a-\frac{I_w}{r}\ddot{\theta}_w-H_L\tag{2.13} Mwx¨=Rr−kmkeθ˙w+RrkmVa−rIwθ¨w−HL(2.13) 对于右轮有: M w x ¨ = − k m k e R r θ ˙ w + k m R r V a − I w r θ ¨ w − H R (2.14) M_w\ddot{x}=\frac{-k_mk_e}{Rr}\dot{\theta}_w+\frac{k_m}{Rr}V_a-\frac{I_w}{r}\ddot{\theta}_w-H_R \tag{2.14} Mwx¨=Rr−kmkeθ˙w+RrkmVa−rIwθ¨w−HR(2.14) 由纯滚动条件得到 θ ¨ w = x ¨ r \ddot{\theta}_w=\frac{\ddot{x}}{r} θ¨w=rx¨ θ ˙ w = x ˙ r (2.15) \dot{\theta}_w=\frac{\dot{x}}{r} \tag{2.15} θ˙w=rx˙(2.15) 代入式 ( 2.13 ) (2.13) (2.13)和 ( 2.14 ) (2.14) (2.14)得到 M w x ¨ = − k m k e R r 2 x ˙ + k m R r V a − I w r 2 x ¨ − H L (2.16) M_w\ddot{x}=\frac{-k_mk_e}{Rr^2}\dot{x}+\frac{k_m}{Rr}V_a-\frac{I_w}{r^2}\ddot{x}-H_L \tag{2.16} Mwx¨=Rr2−kmkex˙+RrkmVa−r2Iwx¨−HL(2.16) M w x ¨ = − k m k e R r 2 x ˙ + k m R r V a − I w r 2 x ¨ − H R (2.17) M_w\ddot{x}=\frac{-k_mk_e}{Rr^2}\dot{x}+\frac{k_m}{Rr}V_a-\frac{I_w}{r^2}\ddot{x}-H_R \tag{2.17} Mwx¨=Rr2−kmkex˙+RrkmVa−r2Iwx¨−HR(2.17) 两式相加得到 2 ( M w + I w r 2 ) x ¨ = − 2 k m k e R r 2 x ˙ + 2 k m R r V a − ( H L + H R ) (2.18) 2(M_w+\frac{I_w}{r^2})\ddot{x}=\frac{-2k_mk_e}{Rr^2}\dot{x}+\frac{2k_m}{Rr}V_a-(H_L+H_R) \tag{2.18} 2(Mw+r2Iw)x¨=Rr2−2kmkex˙+Rr2kmVa−(HL+HR)(2.18) 2.3 车架动力学模型选取车架为研究对象,根据牛顿第二定律列出动力学方程。 (1)受力分析: 
其中 C L C_L CL和 C R C_R CR分别为左右两轮对车身施加的反作用力矩, θ p \theta_p θp为车身偏转角度, θ ˙ p \dot{\theta}_p θ˙p和 θ ¨ p \ddot{\theta}_p θ¨p分别为车身旋转角速度和角加速度, l l l为车轮中心到小车质心的距离, ∑ F x p \sum{F_{xp}} ∑Fxp为垂直车身轴向合力, H L H_L HL和 H R H_R HR分别为左右轮的对车身的反作用力, P L P_L PL和 P R P_R PR分别为左右轮对车身的支持力, M p M_p Mp为车身质量。 (2)水平方向动力学方程: 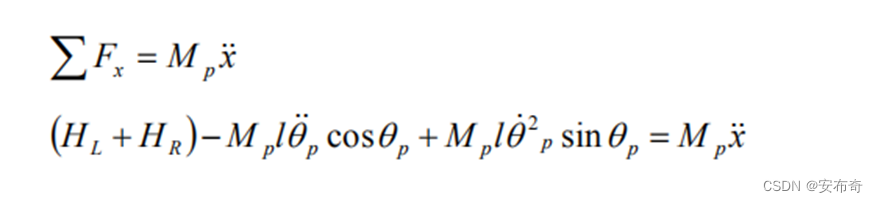 (2.19) (2.19)
因此有 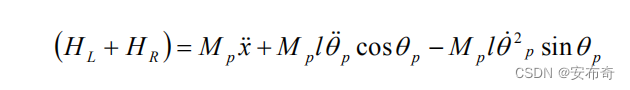 (2.20) (2.20)
(3)垂直车身方向动力学方程: 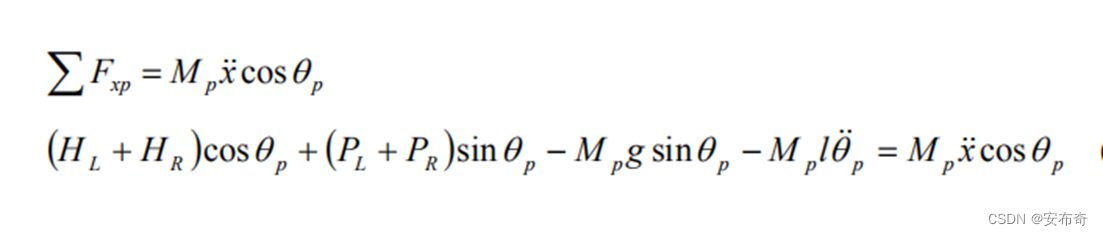 (2.21) (2.21)
(4)绕车身质心转动的动力学方程:  (2.22)
2.4 系统状态方程推导 (2.22)
2.4 系统状态方程推导
为了实现对小车的控制,还需推导系统状态方程,确定状态量和控制输入,这些状态量也是车载传感器的量测目标。根据牛顿第三定律,即左右两轮对车身施加的反作用力矩等于电机对左右两轮的驱动力矩,有 C L + C R = − 2 k m k e R x ˙ r + 2 k m R V a (2.23) C_L+C_R=\frac{-2k_mk_e}{R}\frac{\dot{x}}{r}+\frac{2k_m}{R}V_a \tag{2.23} CL+CR=R−2kmkerx˙+R2kmVa(2.23) 代入式 ( 2.22 ) (2.22) (2.22)得到 − ( H L + H R ) l c o s θ p − ( P L + P R ) l s i n θ p − ( − 2 k m k e R r x ˙ + 2 k m R V a ) = I p θ ¨ p (2.24) -(H_L+H_R)lcos\theta_p-(P_L+P_R)lsin\theta_p-(\frac{-2k_mk_e}{Rr}\dot{x}+\frac{2k_m}{R}V_a)=I_p\ddot{\theta}_p \tag{2.24} −(HL+HR)lcosθp−(PL+PR)lsinθp−(Rr−2kmkex˙+R2kmVa)=Ipθ¨p(2.24) 故有 − ( H L + H R ) l c o s θ p − ( P L + P R ) l s i n θ p = I p θ ¨ p − 2 k m k e R r x ˙ + 2 k m R V a (2.25) -(H_L+H_R)lcos\theta_p-(P_L+P_R)lsin\theta_p=I_p\ddot{\theta}_p -\frac{2k_mk_e}{Rr}\dot{x}+\frac{2k_m}{R}V_a \tag{2.25} −(HL+HR)lcosθp−(PL+PR)lsinθp=Ipθ¨p−Rr2kmkex˙+R2kmVa(2.25) 式 ( 2.21 ) (2.21) (2.21)两边同时乘以 − l -l −l得到 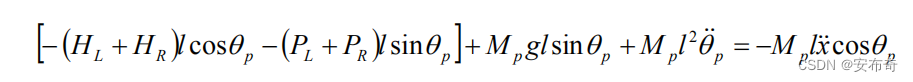 (2.26) (2.26)
式 ( 2.25 ) (2.25) (2.25)代入式 ( 2.26 ) (2.26) (2.26)得到 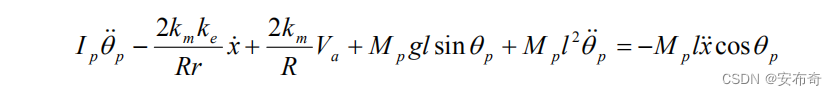 (2.27) (2.27)
将式 ( 2.20 ) (2.20) (2.20)代入式 ( 2.18 ) (2.18) (2.18)消去 ( H L + H R ) (H_L+H_R) (HL+HR)得到  (2.28) (2.28)
式 ( 2.27 ) (2.27) (2.27)和 ( 2.28 ) (2.28) (2.28)可以整理为 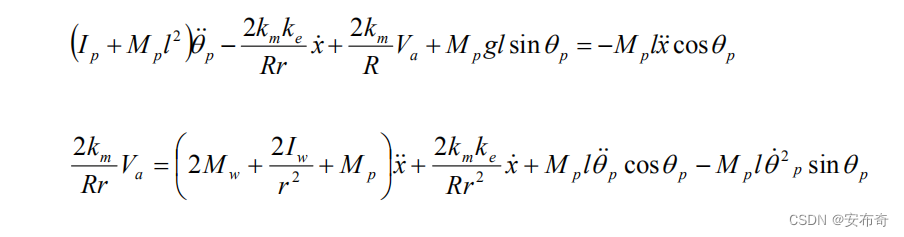 (2.29) (2.29)
假设 θ p = π + ϕ \theta_p=\pi+\phi θp=π+ϕ, ϕ \phi ϕ为偏离垂直方向的一个小角度,则有 c o s θ p ≈ − 1 , s i n θ p ≈ − ϕ , ( d θ p d t ) 2 ≈ 0 (2.30) cos\theta_p\approx-1,sin\theta_p\approx-\phi,(\frac{d\theta_p}{dt})^2\approx0 \tag{2.30} cosθp≈−1,sinθp≈−ϕ,(dtdθp)2≈0(2.30) 代入式(2.29)可以得到线性化的动力学方程,  (2.31) (2.31)
以位移 x x x,速度 x ˙ \dot{x} x˙,车身偏转角度 θ p \theta_p θp 和 角速度 θ p ˙ \dot{\theta_p} θp˙为状态量,电机电压 V a V_a Va为输入,可以列出系统的状态方程为 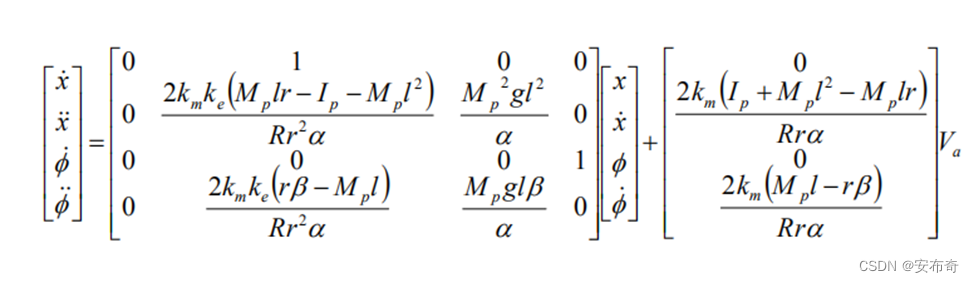 (2.32)
其中, (2.32)
其中,
β = ( 2 M w ) + 2 I w r 2 + M p α = [ I p β + 2 M p l 2 ( M w + I w r 2 ) ] (2.33) \beta=(2M_w)+\frac{2I_w}{r^2}+M_p\\\alpha=[I_p\beta+2M_pl^2(M_w+\frac{I_w}{r^2}) ]\tag{2.33} β=(2Mw)+r22Iw+Mpα=[Ipβ+2Mpl2(Mw+r2Iw)](2.33) 3.状态反馈的LQR设计线性二次调节器(LQR)是一种现代控制理论方法,用于设计具有二次型性能指标的线性时不变系统的最优控制器。设有以下线性系统: x ( t ) ˙ = A x ( t ) + B u ( t ) x ( 0 ) = x 0 (3.1) \dot{x(t)}=Ax(t)+Bu(t) \\ x(0)=x_0 \tag{3.1} x(t)˙=Ax(t)+Bu(t)x(0)=x0(3.1) 式中 A A A为系统矩阵, B B B为输入矩阵, x 0 x_0 x0是系统初始状态。在LQR中,若控制输入和状态不存在直接耦合(存在耦合就在积分项内加上 x T N u x^TNu xTNu, N N N为耦合矩阵),则系统的性能指标常用一个积分函数进行表示: J = ∫ 0 ∞ [ x T ( t ) Q x ( t ) + u T ( t ) R u ( t ) ] d t (3.2) J=\int^{\infty}_0[x^T(t)Qx(t)+u^T(t)Ru(t)]dt\tag{3.2} J=∫0∞[xT(t)Qx(t)+uT(t)Ru(t)]dt(3.2) 式(2.35)中的性能指标函数由两部分组成: 状态误差的二次代价 x T ( t ) Q x ( t ) x^T(t)Qx(t) xT(t)Qx(t):衡量系统状态 x ( t ) x(t) x(t)与其理想状态(通常是原点)之间偏差的平方。其中 Q Q Q为正定矩阵,用来量化不同状态变量之间偏差的重要性。如果某个状态变量的偏差对系统性能影响更大,则 Q Q Q阵中相应的对角元素就会较大,通过优化这个项,我们希望系统状态能尽可能接近期望的状态或保持稳定。控制输入的二次代价 u T ( t ) R u ( t ) u^T(t)Ru(t) uT(t)Ru(t):反映了控制输入 u ( t ) u(t) u(t)的能量消耗或控制努力的成本。 R R R是一个正定矩阵,用来权衡不同控制输入分量的成本。较大的 R R R值意味着对相应控制输入的使用会增加更多的成本,鼓励控制器寻找更经济或更平缓的控制策略。详细的LQR推导参考:https://blog.csdn.net/zjh2883/article/details/136167154,在此仅给出简要过程 LQR的目标找到一个状态反馈控制器,根据状态反馈 x x x来获得控制输入 u = − K x (3.3) u=-Kx\tag{3.3} u=−Kx(3.3) 从而最小化系统的性能指标函数 J J J。其中 K = R − 1 B P K=R^{-1}BP K=R−1BP, P P P为常量对称矩阵,可以通过求解下列Riccati矩阵方程得到, P A + A T P − P B R − 1 B T P + Q = 0 (3.4) PA+A^TP-PBR^{-1}B^TP+Q=0\tag{3.4} PA+ATP−PBR−1BTP+Q=0(3.4) 给定
A
A
A、
B
B
B、
Q
Q
Q和
R
R
R可解出
P
P
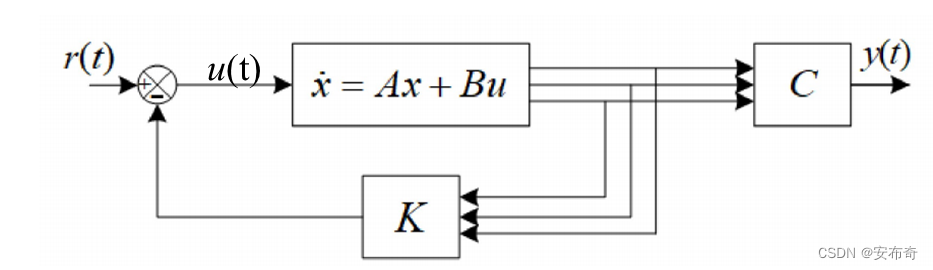
P,从而解出控制输入。直接状态反馈LQR控制的系统框图如下: 代入系统状态方程得到系统矩阵 A A A和输入矩阵 B B B为  (3.5)
(3.5)
系统的输出方程为  (3.6)
(3.6)
系统能进行状态反馈控制的充要条件是系统能控能观,则用MATLAB来检查系统的能控性和能观性,即可控矩阵和可观矩阵的秩是否等于状态变量个数: %能控性判断 rank(ctrb(A,B))==4; %能观性判断 rank(obsv(A,C))==4;检查完能控性和能观性后,调用MATLAB lqr函数来求解状态反馈增益矩阵: A=[0,1,0,0;0,-0.0097,11.159,0;0,0,0,1;0,-0.0293,172.1160,0]; B=[0;0.0815;0;0.2456]; C=[1,0,0,0;0,1,0,0;0,0,1,0;0,0,0,1]; D=[0;0;0;0]; % 系统状态方程 sys=ss(A,B,C,D); Q=[100 0 0 0;zeros(1,4);0 0 20 0;zeros(1,4)]; R=20; N=0; % 求解状态反馈增益矩阵 [K,P,E] =lqr(sys,Q,R,N);其中 K K K即为状态反馈增益矩阵, P P P即为Riccati 方程的解矩阵, E E E是一个MATLAB设置的一个拓展输出,有些特定问题可能会用到,这里没有用到 E E E。 4.输出反馈的LQR设计参考:符新东,张大兴,袁帅.两轮自平衡小车的状态反馈和输出反馈控制[J].仪表技术与传感器,2018,(08):90-93. 在工程应用中,如果无法实时获取系统的全部状态量,则需要设计状态观测器,根据系统输出量来估计状态量(系统要满足能观性),从而得到控制输入。设系统状态估计为 x ^ \hat{x} x^,则控制输入为 u = − K x ^ u=-K\hat{x} u=−Kx^,此时系统状态方程满足: 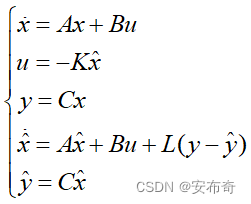 (4.1)
(4.1)
其中
x
^
˙
=
A
x
^
+
B
u
+
L
(
y
−
y
^
)
\dot{\hat{x}}=A\hat{x}+Bu+L(y-\hat{y})
x^˙=Ax^+Bu+L(y−y^)为观测器的状态方程,
y
^
=
C
x
^
\hat{y}=C\hat{x}
y^=Cx^为观测器的输出方程。输出反馈LQR的系统框图如下: 这是齐次微分方程,解为 e x ( t ) = e ( A − L C ) t e x ( 0 ) e_x(t)=e^{(A-LC)t}e_x(0) ex(t)=e(A−LC)tex(0),则如果 A − L C A-LC A−LC稳定,即矩阵的特征根都是负实部,则 t t t趋于无穷时状态估计误差也趋于0,则可以通过极点配置法,即求合适的 L L L让 A − L C A-LC A−LC的极点位于指定位置,当然,自由配置极点的充要条件是 A − L C A-LC A−LC满秩,即系统是能控的。指定4个极点,采用MATLAB的place函数来求解满足要求的 L L L阵: p1=-130; p2=-140; p3=-150; p4=-160; L=place(A',C',[p1 p2 p3 p4]);求得满足要求的 L L L为:  (3.6)
(3.6)
|
【本文地址】

 给定平衡小车参数:车轮半径
r
=
0.051
m
r=0.051m
r=0.051m,车轮绕中心的转动惯量
I
w
=
0.000039
k
g
⋅
m
2
I_w=0.000039kg\cdot m^2
Iw=0.000039kg⋅m2,车轮质量
M
w
=
0.03
k
g
M_w=0.03kg
Mw=0.03kg,直流电机电阻
R
=
3
Ω
R=3\Omega
R=3Ω,车身绕质心的转动惯量
I
p
=
0.0041
k
g
⋅
m
2
I_p=0.0041kg\cdot m^2
Ip=0.0041kg⋅m2,车身质量
M
p
=
1.13
k
g
M_p=1.13kg
Mp=1.13kg,电机的力矩常数
K
m
=
0.006123
N
m
/
A
K_m=0.006123Nm/A
Km=0.006123Nm/A,电机的感应电动势系数
K
e
=
0.006087
V
⋅
s
/
r
a
d
K_e=0.006087V\cdot s/rad
Ke=0.006087V⋅s/rad,重力加速度
g
=
9.81
m
/
s
2
g=9.81m/s^2
g=9.81m/s2,车轮中心到小车质心的距离
l
=
0.2
m
l=0.2m
l=0.2m。
给定平衡小车参数:车轮半径
r
=
0.051
m
r=0.051m
r=0.051m,车轮绕中心的转动惯量
I
w
=
0.000039
k
g
⋅
m
2
I_w=0.000039kg\cdot m^2
Iw=0.000039kg⋅m2,车轮质量
M
w
=
0.03
k
g
M_w=0.03kg
Mw=0.03kg,直流电机电阻
R
=
3
Ω
R=3\Omega
R=3Ω,车身绕质心的转动惯量
I
p
=
0.0041
k
g
⋅
m
2
I_p=0.0041kg\cdot m^2
Ip=0.0041kg⋅m2,车身质量
M
p
=
1.13
k
g
M_p=1.13kg
Mp=1.13kg,电机的力矩常数
K
m
=
0.006123
N
m
/
A
K_m=0.006123Nm/A
Km=0.006123Nm/A,电机的感应电动势系数
K
e
=
0.006087
V
⋅
s
/
r
a
d
K_e=0.006087V\cdot s/rad
Ke=0.006087V⋅s/rad,重力加速度
g
=
9.81
m
/
s
2
g=9.81m/s^2
g=9.81m/s2,车轮中心到小车质心的距离
l
=
0.2
m
l=0.2m
l=0.2m。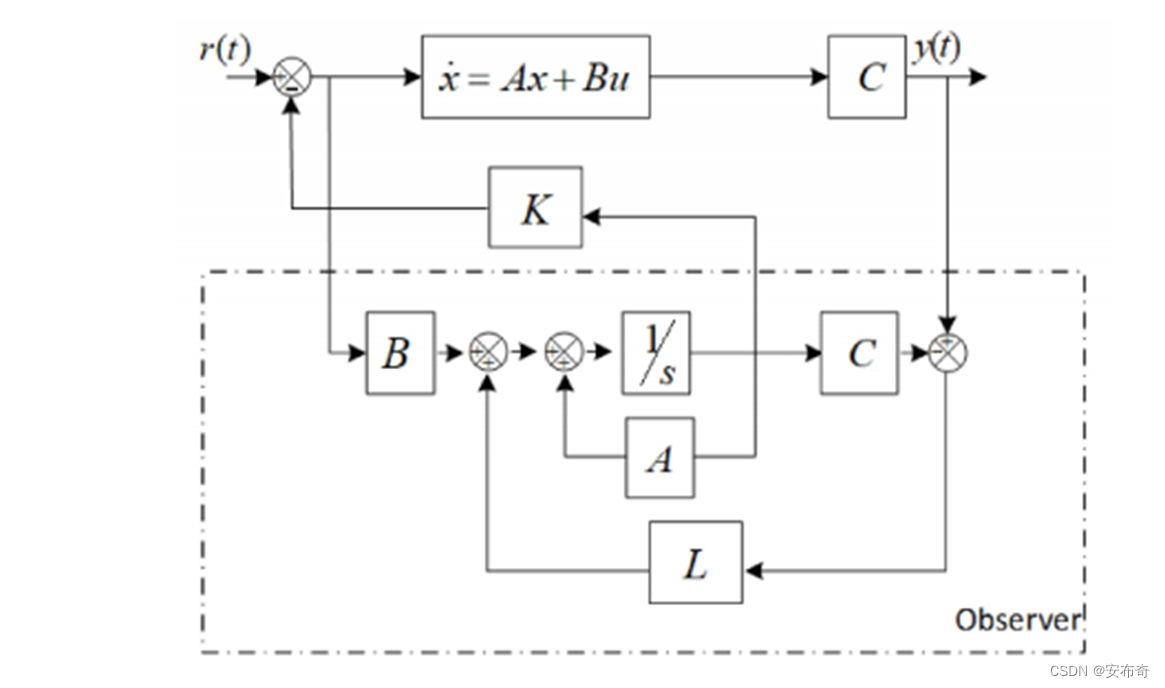 状态观测器的设计目标是寻找合适的观测器增益矩阵
L
L
L,使得状态估计误差
e
x
(
t
)
=
x
(
t
)
−
x
^
(
t
)
e_x(t)=x(t)-\hat{x}(t)
ex(t)=x(t)−x^(t)渐进收敛至0,此时有
y
−
y
^
=
0
y-\hat{y}=0
y−y^=0,即观测器的系统状态方程和被观测对象的系统状态方程完全一致。状态估计误差对时间求导得到动态估计误差方程为
e
x
˙
(
t
)
=
(
A
−
L
C
)
e
x
(
t
)
(4.2)
\dot{e_x}(t)=(A-LC)e_x(t)\tag{4.2}
ex˙(t)=(A−LC)ex(t)(4.2)
状态观测器的设计目标是寻找合适的观测器增益矩阵
L
L
L,使得状态估计误差
e
x
(
t
)
=
x
(
t
)
−
x
^
(
t
)
e_x(t)=x(t)-\hat{x}(t)
ex(t)=x(t)−x^(t)渐进收敛至0,此时有
y
−
y
^
=
0
y-\hat{y}=0
y−y^=0,即观测器的系统状态方程和被观测对象的系统状态方程完全一致。状态估计误差对时间求导得到动态估计误差方程为
e
x
˙
(
t
)
=
(
A
−
L
C
)
e
x
(
t
)
(4.2)
\dot{e_x}(t)=(A-LC)e_x(t)\tag{4.2}
ex˙(t)=(A−LC)ex(t)(4.2)