| Mathematica对函数表达式求导并设置为新的自定义函数 | 您所在的位置:网站首页 › 带有绝对值函数求导 › Mathematica对函数表达式求导并设置为新的自定义函数 |
Mathematica对函数表达式求导并设置为新的自定义函数
|
自定义函数
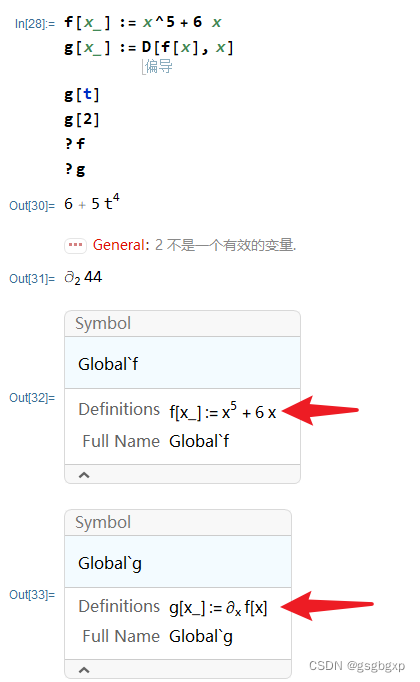
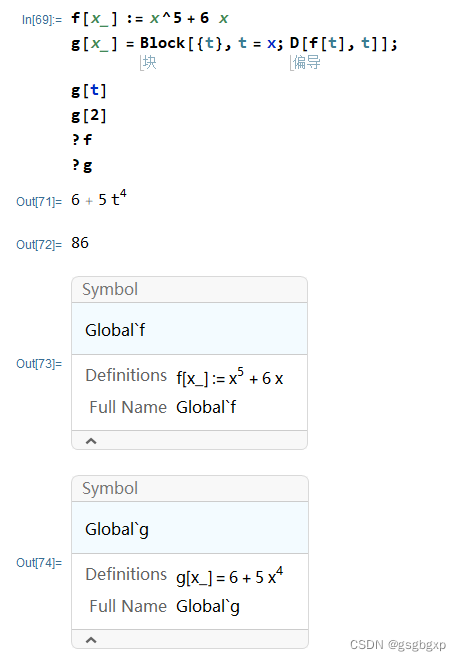
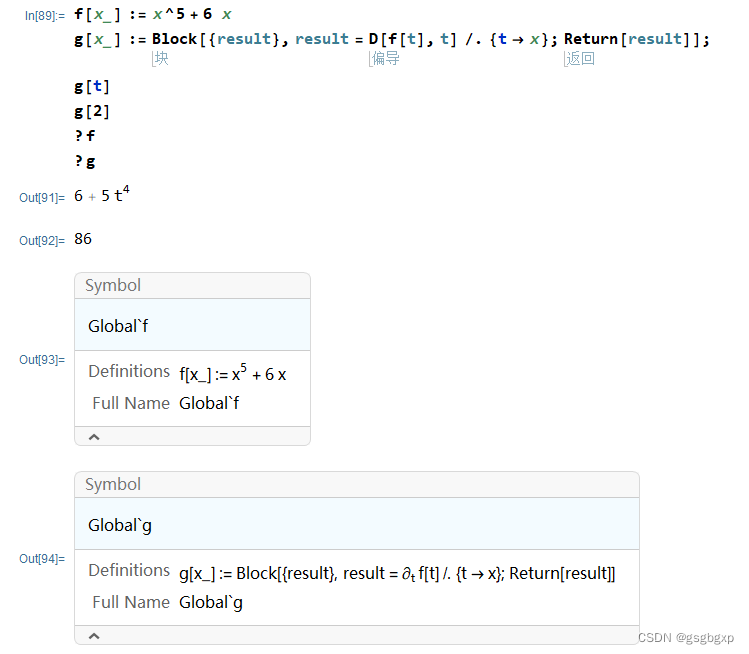
自定义函数需要注意亮点 1、最好使用 := 而非 = 2、定义时等式左端函数变量有下划线,被称为“空白” Wolfram 系统变换规则最强有力的方面或许是它们不仅能用于表达式,而且能用于模式(patterns). 模式是一个诸如f[t_] 这样的包含下划线的表达式. 下划线可以代表任何表达式. 这样,对 f[t_] 的变换规则将变换具有任何 自变量的函数 f. 注意,作为对照,对不带有下划线的 f[x] 的变换规则只变换表达式 f[x],而对诸如 f[y] 等表达式没有任何作用. 当用户定义一个函数,例如 f[t_]:=t^2 时,所做的事情是告诉 Wolfram 系统,在任何可能的时候,自动使用变换规则f[t_]->t^2. (引自MMA教程“函数的变换规则”) 定义函数后可以对变量赋值,也可以作图 f2[t_] := t^3 f2[3] f2[a] Plot[f2[t], {t, 0, 3}] 对函数表达式求导这个操作相对简单,直接用 D[f,x] 或 D[f,{x,n}],分别代表求偏导数和高阶导数。 下面给出例子 f[x_] := x^5 + 6 x D[x^5 + 6 x, x] D[f[x], x] D[f[t], t]运行结果为 有的时候希望能把求导的结果存为一个新的自定义函数,以方便后期使用。 一个直观但是错误的方法是 从上图看出,g[t]的结果似乎没问题,但g[3]的结果就不太对了。 这里的原因在于 给x赋值时原函数f里的x也被赋值了。 查看 f 和 g 可以发现g并不是一个独立的函数,而是要先把变量代入f,然后再求导。所以对于g[2]而言,就相当于求 D[f(2),2],这就不合理了。 下面提供了4个方案,其中前两个方案感觉最优。 解决方案1在自定义函数时一般习惯用 :=,而此处恰恰改用 = 就能解决问题。即 f[x_] := x^5 + 6 x g[x_] = D[f[x], x] g[t] g[2]结果如下 使用Block(块) Block[{x,y,...},expr] ,意为指定用符号 x、y、… 的局部值计算 expr. f[x_] := x^5 + 6 x g[x_] = Block[{t}, t = x; D[f[t], t]]; (*注意这里用的是=*) g[t] g[2]结果如下 与上一解决方案类似,注意这里用的是 := f[x_] := x^5 + 6 x g[x_] := Block[{result}, result = D[f[t], t] /. {t -> x}; Return[result]]; g[t] g[2]
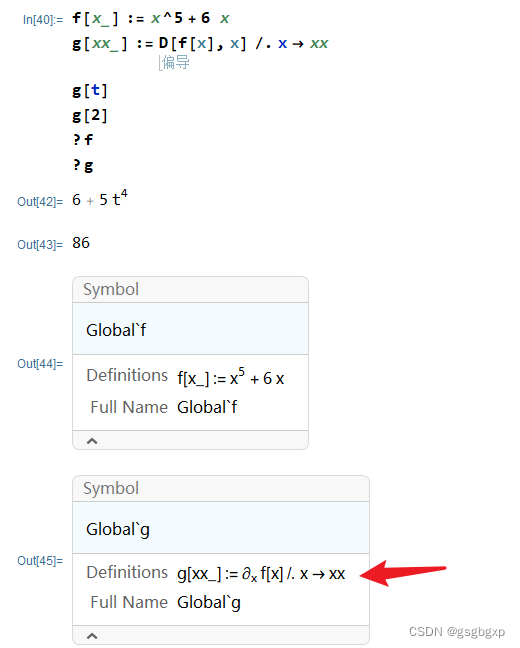
既然问题的原因在于x的赋值上,那么就改变变量名。 但这样的缺点就在于函数多了那自变量名也多了。 f[x_] := x^5 + 6 x g[xx_] := D[f[x], x] /. x -> xx g[t] g[2]结果如下 |
【本文地址】
| 今日新闻 |
| 推荐新闻 |
| 专题文章 |