数学建模

差分算法是数学建模比赛中的一种十分常见的代码，在2018A题和2020A中均用到一维热传导模型，模型的求解用的就是差分算法，具体如何解可以自己去查看相关论文。

差分方法又称为有限差分方法或网格法，是求偏微分方程定解问题的数值解中应用 最广泛的方法之一。它的基本思想是：先对求解区域作网格剖分，将自变量的连续变化 区域用有限离散点（网格点）集代替；将问题中出现的连续变量的函数用定义在网格点 上离散变量的函数代替；通过用网格点上函数的差商代替导数，将含连续变量的偏微分 方程定解问题化成只含有限个未知数的代数方程组（称为差分格式）。如果差分格式有 解，且当网格无限变小时其解收敛于原微分方程定解问题的解，则差分格式的解就作为 原问题的近似解（数值解）。因此，用差分方法求偏微分方程定解问题一般需要解决一下问题：

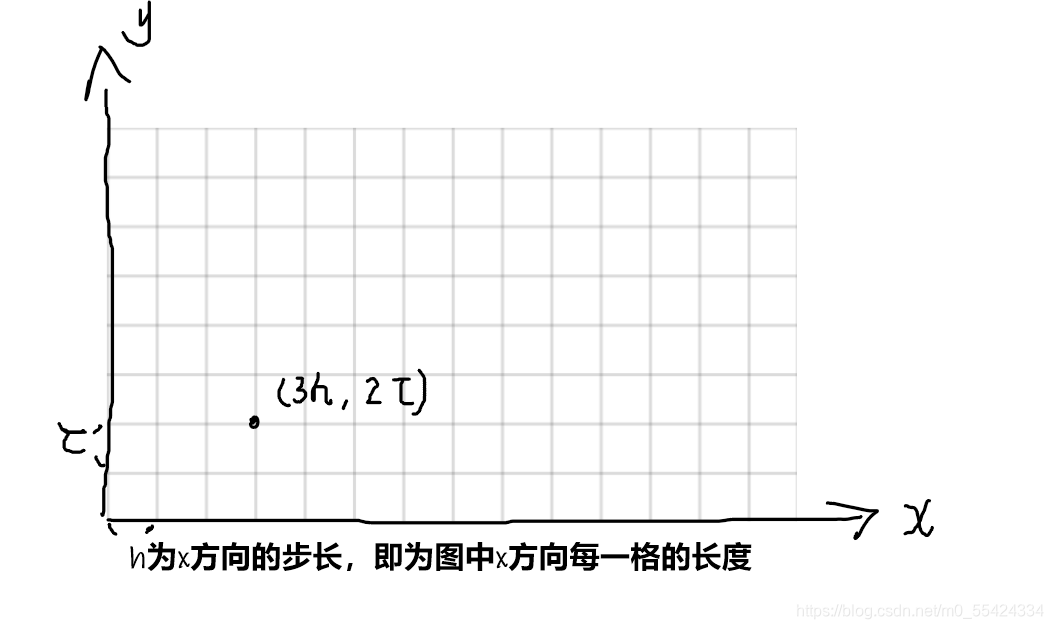
因此，只要确定了步长，我们就可以将连续变化的自变量用有限离散点来表示

对于(9-3)的式子，为了方便计算，我们用差分来表示偏微分方程 ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = f ( x , y ) \frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}=f(x,y) ∂x2∂2u​+∂y2∂2u​=f(x,y) 由于式子中进行了两次偏导，因此我们一步一步进行分析。

进行一次差分，我们用向前差分。 ∂ u ∂ x = u ( k + 1 , j ) − u ( k , j ) h \frac{\partial u}{\partial x}=\frac{u(k+1,j)-u(k,j)}{h} ∂x∂u​=hu(k+1,j)−u(k,j)​ 由于向前差分有误差，如果我们进行两次向前差分的话，计算的误差可能会增大，因此，第二次偏导我们选择向后差分。即我们混合向前差分、向后差分来近似代替两次偏导。

因此，第二次我们用向后差分 ∂ 2 u ∂ x 2 = ∂ ∂ x ( u ( k + 1 , j ) − u ( k , j ) h ) = ∂ ∂ x ( u ( k + 1 , j ) h ) − ∂ ∂ x ( u ( k , j ) h ) \begin{aligned} \frac{\partial^2u}{\partial x^2}&=\frac{\partial}{\partial x}(\frac{u(k+1,j)-u(k,j)}{h})\\ & = \frac{\partial}{\partial x}(\frac{u(k+1,j)}{h})-\frac{\partial}{\partial x}(\frac{u(k,j)}{h}) \end{aligned} ∂x2∂2u​​=∂x∂​(hu(k+1,j)−u(k,j)​)=∂x∂​(hu(k+1,j)​)−∂x∂​(hu(k,j)​)​

∂ ∂ x ( u ( k + 1 , j ) h ) = u ( k + 1 , j ) − u ( k , j ) h ⋅ h − 0 h 2 = u ( k + 1 , j ) − u ( k , j ) h 2 \begin{aligned} \frac{\partial}{\partial x}(\frac{u(k+1,j)}{h})&=\frac{\frac{u(k+1,j)-u(k,j)}{h}\cdot h-0}{h^2}\\ &=\frac{u(k+1,j)-u(k,j)}{h^2} \end{aligned} ∂x∂​(hu(k+1,j)​)​=h2hu(k+1,j)−u(k,j)​⋅h−0​=h2u(k+1,j)−u(k,j)​​

∂ ∂ x ( u ( k , j ) h ) = u ( k , j ) − u ( k − 1 , j ) h ⋅ h − 0 h 2 = u ( k , j ) − u ( k − 1 , j ) h 2 \begin{aligned} \frac{\partial}{\partial x}(\frac{u(k,j)}{h})&=\frac{\frac{u(k,j)-u(k-1,j)}{h}\cdot h-0}{h^2}\\ &=\frac{u(k,j)-u(k-1,j)}{h^2} \end{aligned} ∂x∂​(hu(k,j)​)​=h2hu(k,j)−u(k−1,j)​⋅h−0​=h2u(k,j)−u(k−1,j)​​ 综上， ∂ 2 u ∂ x 2 = ∂ ∂ x ( u ( k + 1 , j ) − u ( k , j ) h ) = ∂ ∂ x ( u ( k + 1 , j ) h ) − ∂ ∂ x ( u ( k , j ) h ) = u ( k + 1 , j ) − u ( k , j ) h 2 − u ( k , j ) − u ( k − 1 , j ) h 2 = u ( k + 1 , j ) − 2 u ( k , j ) + u ( k − 1 , j ) h 2 \begin{aligned} \frac{\partial^2u}{\partial x^2}&=\frac{\partial}{\partial x}(\frac{u(k+1,j)-u(k,j)}{h})\\ & = \frac{\partial}{\partial x}(\frac{u(k+1,j)}{h})-\frac{\partial}{\partial x}(\frac{u(k,j)}{h})\\ &=\frac{u(k+1,j)-u(k,j)}{h^2}-\frac{u(k,j)-u(k-1,j)}{h^2}\\ &= \frac{u(k+1,j)-2u(k,j)+u(k-1,j)}{h^2} \end{aligned} ∂x2∂2u​​=∂x∂​(hu(k+1,j)−u(k,j)​)=∂x∂​(hu(k+1,j)​)−∂x∂​(hu(k,j)​)=h2u(k+1,j)−u(k,j)​−h2u(k,j)−u(k−1,j)​=h2u(k+1,j)−2u(k,j)+u(k−1,j)​​ 同理可得 ∂ 2 u ∂ y 2 = u ( k , j + 1 ) − 2 u ( k , j ) + u ( k , j − 1 ) τ 2 \frac{\partial^2u}{\partial y^2}=\frac{u(k,j+1)-2u(k,j)+u(k,j-1)}{\tau^2} ∂y2∂2u​=τ2u(k,j+1)−2u(k,j)+u(k,j−1)​ 所以原方程就变为 ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = f ( x , y ) u ( k + 1 , j ) − 2 u ( k , j ) + u ( k − 1 , j ) h 2 + u ( k , j + 1 ) − 2 u ( k , j ) + u ( k , j − 1 ) τ 2 = f ( x , y ) \frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}=f(x,y)\\ \frac{u(k+1,j)-2u(k,j)+u(k-1,j)}{h^2}+\frac{u(k,j+1)-2u(k,j)+u(k,j-1)}{\tau^2}=f(x,y) ∂x2∂2u​+∂y2∂2u​=f(x,y)h2u(k+1,j)−2u(k,j)+u(k−1,j)​+τ2u(k,j+1)−2u(k,j)+u(k,j−1)​=f(x,y) 以上的进行通过混合向前差分、向后差分的方法求二阶偏导的方法实际上就是二阶中心差分

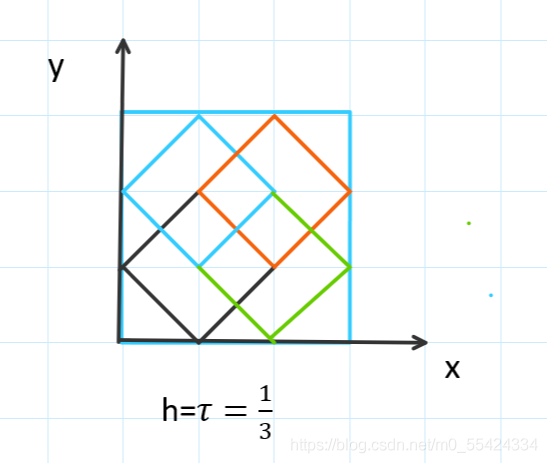
函数的前向差分通常简称为函数的差分。对于函数f(x)，如果在等距节点： x k = x 0 + k h ( k = 0 , 1 , ⋯   , n ) x_k=x_0+kh(k=0,1,\cdots,n) xk​=x0​+kh(k=0,1,⋯,n)

Δ f ( x k ) = f ( x k + 1 ) − f ( x k ) \Delta f(x_k)=f(x_{k+1})-f(x_k) Δf(xk​)=f(xk+1​)−f(xk​)

则称Δf(x)，函数在每个小区间上的增量 y ( k + 1 ) − y ( k ) y(k+1)-y(k) y(k+1)−y(k)为f(x)的一阶前向差分。在微积分学中的有限差分（finite differences），前向差分通常是微分在离散的函数中的等效运算。差分方程的解法也与微分方程的解法相似。当是多项式时，前向差分为Delta算子，一种线性算子。前向差分会将多项式阶数降低1 由于向前差分可以从已知的值求解出结果，所以我们称向前差分为显式差分。

向后差分为隐式差分方法，无条件稳定。 对于函数 f ( x k ) f(x_k) f(xk​)，一阶向后差分为： Δ f ( x k ) = f ( x k ) − f ( x k − 1 ) \Delta f(x_k)=f(x_k)-f(x_{k-1}) Δf(xk​)=f(xk​)−f(xk−1​)

Crank-Nicolson差分格式又称为中心差分格式。Crank-Nicolson方法式显式方法和隐式方法的结合，式无条件稳定的方法，公式看起来复杂，但是考虑到提高的精度和保证的稳定性。 Δ f ( x k ) = 1 2 ( f ( x k + 1 ) − f ( x k ) + f ( x k ) − f ( x k − 1 ) ) = 1 2 ( f ( x k + 1 ) − f ( x k − 1 ) ) \begin{aligned} \Delta f(x_k)&=\frac{1}{2}(f(x_{k+1})-f(x_k)+f(x_k)-f(x_{k-1}))\\ &=\frac{1}{2}(f(x_{k+1})-f(x_{k-1})) \end{aligned} Δf(xk​)​=21​(f(xk+1​)−f(xk​)+f(xk​)−f(xk−1​))=21​(f(xk+1​)−f(xk−1​))​ 对于扩散方程（包括许多其他方程），可以证明Crank-Nicolson方法无条件稳定。但是，如果时间步长与空间步长平方的比值过大（一般地，大于1/2），近似解中将存在虚假的振荡或衰减。基于这个原因，当要求大时间步或高空间分辨率的时候，往往会采用数值精确较差的后向欧拉方法进行计算，这样即可以保证稳定，又避免了解的伪振荡。

用五点菱形个格式求解Laplace方程第一边值问题 { ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 = 0 , ( x , y ) ∈ Ω u ( x , y ) ∣ ( x , y ) ∈ Γ = lg ⁡ [ ( 1 + x ) 2 + y 2 ] , Γ = ∂ Ω , \begin{cases} \frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}=0,&(x,y)\in \Omega\\ u(x,y)|_{(x,y)\in \Gamma}=\lg [(1+x)^2+y^2],&\Gamma=\partial \Omega, \end{cases} {∂x2∂2u​+∂y2∂2u​=0,u(x,y)∣(x,y)∈Γ​=lg[(1+x)2+y2],​(x,y)∈ΩΓ=∂Ω,​ 其中 Ω = { ( x , y ) ∣ 0 ≤ x , y ≤ 1 } \Omega=\left\{ (x,y)|0 \leq x,y \leq 1 \right\} Ω={(x,y)∣0≤x,y≤1}，取 h = τ = 1 3 h=\tau=\frac{1}{3} h=τ=31​

解：

根据题意，我们画出网格出来，正好构成四个五点菱形，即得到四个方程，我们将线性方程组写出来 { 1 h 2 ( u 1 , 2 + u 2 , 1 + u 1 , 0 + u 0 , 1 − 4 u ( 1 , 1 ) ) = 0 1 h 2 ( u 2 , 2 + u 3 , 1 + u 2 , 0 + u 1 , 1 − 4 u ( 2 , 1 ) ) = 0 1 h 2 ( u 1 , 3 + u 2 , 2 + u 1 , 1 + u 0 , 2 − 4 u ( 1 , 2 ) ) = 0 1 h 2 ( u 2 , 3 + u 3 , 2 + u 2 , 1 + u 1 , 2 − 4 u ( 2 , 2 ) ) = 0 \begin{cases} \frac{1}{h^2}(u_{1,2}+u_{2,1}+u_{1,0}+u_{0,1}-4u(1,1))=0\\ \frac{1}{h^2}(u_{2,2}+u_{3,1}+u_{2,0}+u_{1,1}-4u(2,1))=0\\ \frac{1}{h^2}(u_{1,3}+u_{2,2}+u_{1,1}+u_{0,2}-4u(1,2))=0\\ \frac{1}{h^2}(u_{2,3}+u_{3,2}+u_{2,1}+u_{1,2}-4u(2,2))=0 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧​h21​(u1,2​+u2,1​+u1,0​+u0,1​−4u(1,1))=0h21​(u2,2​+u3,1​+u2,0​+u1,1​−4u(2,1))=0h21​(u1,3​+u2,2​+u1,1​+u0,2​−4u(1,2))=0h21​(u2,3​+u3,2​+u2,1​+u1,2​−4u(2,2))=0​ 线性方程组又可以化简成 [ − 4 1 1 0 1 − 4 0 1 1 0 − 4 1 0 1 1 − 4 ] [ u 1 , 1 u 1 , 2 u 2 , 1 u 2 , 2 ] = − [ u 1 , 0 + u 0 , 1 u 3 , 1 + u 2 , 0 u 1 , 3 + u 0 , 2 u 2 , 3 + u 3 , 2 ] \begin{bmatrix} -4 & 1 &1 &0 \\ 1 & -4 & 0 & 1 \\ 1 & 0 & -4 & 1\\ 0 & 1 & 1 & -4 \end{bmatrix} \begin{bmatrix} u_{1,1}\\ u_{1,2}\\ u_{2,1}\\ u_{2,2} \end{bmatrix}=- \begin{bmatrix} u_{1,0}+u_{0,1}\\ u_{3,1}+u_{2,0}\\ u_{1,3}+u_{0,2}\\ u_{2,3}+u_{3,2} \end{bmatrix} ⎣⎢⎢⎡​−4110​1−401​10−41​011−4​⎦⎥⎥⎤​⎣⎢⎢⎡​u1,1​u1,2​u2,1​u2,2​​⎦⎥⎥⎤​=−⎣⎢⎢⎡​u1,0​+u0,1​u3,1​+u2,0​u1,3​+u0,2​u2,3​+u3,2​​⎦⎥⎥⎤​

解非齐次线性方程组求得： u 1 = 0.6348 , u 2 = 1.06 , u 3 = 0.7985 , u 4 = 1.1698 u_1=0.6348, u_2=1.06, u_3=0.7985, u_4=1.1698 u1​=0.6348,u2​=1.06,u3​=0.7985,u4​=1.1698 计算的MATLAB程序如下

代码解读

观察线性方程： [ − 4 1 1 0 1 − 4 0 1 1 0 − 4 1 0 1 1 − 4 ] [ u 1 , 1 u 1 , 2 u 2 , 1 u 2 , 2 ] = − [ u 1 , 0 + u 0 , 1 u 3 , 1 + u 2 , 0 u 1 , 3 + u 0 , 2 u 2 , 3 + u 3 , 2 ] \begin{bmatrix} -4 & 1 &1 &0 \\ 1 & -4 & 0 & 1 \\ 1 & 0 & -4 & 1\\ 0 & 1 & 1 & -4 \end{bmatrix} \begin{bmatrix} u_{1,1}\\ u_{1,2}\\ u_{2,1}\\ u_{2,2} \end{bmatrix}=- \begin{bmatrix} u_{1,0}+u_{0,1}\\ u_{3,1}+u_{2,0}\\ u_{1,3}+u_{0,2}\\ u_{2,3}+u_{3,2} \end{bmatrix} ⎣⎢⎢⎡​−4110​1−401​10−41​011−4​⎦⎥⎥⎤​⎣⎢⎢⎡​u1,1​u1,2​u2,1​u2,2​​⎦⎥⎥⎤​=−⎣⎢⎢⎡​u1,0​+u0,1​u3,1​+u2,0​u1,3​+u0,2​u2,3​+u3,2​​⎦⎥⎥⎤​ 这个形式为最小二乘法的形式

参考Matlab中的线性最小二乘的标准型： min ⁡ A ∥ R A − Y ∥ 2 2 \min _A \Vert RA-Y \Vert_2^2 Amin​∥RA−Y∥22​ 所以我们只需要求出等式右边的式子，那么我们就可以解出等式中间的向量

现在我们来解等式右边的向量，观察可知，为定义域的边界

注意这里从1开始，与上式子有些不同 [ u 1 , 1 u 1 , 2 u 1 , 3 u 1 , 4 u 2 , 1 u 2 , 2 u 2 , 3 u 2 , 4 u 3 , 1 u 3 , 2 u 3 , 3 u 3 , 4 u 4 , 1 u 4 , 2 u 4 , 3 u 4 , 4 ] \begin{bmatrix} u_{1,1} & u_{1,2} & u_{1,3} & u_{1,4}\\ u_{2,1} & u_{2,2} & u_{2,3} & u_{2,4}\\ u_{3,1} & u_{3,2} & u_{3,3} & u_{3,4}\\ u_{4,1} & u_{4,2} & u_{4,3} & u_{4,4} \end{bmatrix} ⎣⎢⎢⎡​u1,1​u2,1​u3,1​u4,1​​u1,2​u2,2​u3,2​u4,2​​u1,3​u2,3​u3,3​u4,3​​u1,4​u2,4​u3,4​u4,4​​⎦⎥⎥⎤​ 因此我们只需要解出边界的值，就可以把b表示出来

同 [ u 1 , 1 u 1 , 2 u 1 , 3 u 1 , 4 u 2 , 1 u 2 , 2 u 2 , 3 u 2 , 4 u 3 , 1 u 3 , 2 u 3 , 3 u 3 , 4 u 4 , 1 u 4 , 2 u 4 , 3 u 4 , 4 ] \begin{bmatrix} u_{1,1} & u_{1,2} & u_{1,3} & u_{1,4}\\ u_{2,1} & u_{2,2} & u_{2,3} & u_{2,4}\\ u_{3,1} & u_{3,2} & u_{3,3} & u_{3,4}\\ u_{4,1} & u_{4,2} & u_{4,3} & u_{4,4} \end{bmatrix} ⎣⎢⎢⎡​u1,1​u2,1​u3,1​u4,1​​u1,2​u2,2​u3,2​u4,2​​u1,3​u2,3​u3,3​u4,3​​u1,4​u2,4​u3,4​u4,4​​⎦⎥⎥⎤​ 因此我们只需要解出边界的值，就可以把b表示出来，然后用最小二乘法解出中间的变量，那么每个点值都接出来了。

参考文献：数值分析（原书第2版）_Timothy Sauer_机械工业出版社