| 第一篇:为什么需要小波变换 | 您所在的位置:网站首页 › 小波变换的应用 › 第一篇:为什么需要小波变换 |
第一篇:为什么需要小波变换
 利用小波分析解决工程问题指南!
利用小波分析解决工程问题指南!
本系列文章主要翻译自Robi Polikar的The Wavelet Tutorial并进行了一些顺序调整,对于笔者自己添加的内容,将处理成本段话的形式,即放在引用中。 欢迎来到这个关于小波变换的入门教程。 整体来说,小波变换还是一个相对冷门的技术,并且很多与之相关的教程、资料都是给专业人士看的,这对于想使用小波变换来解决工程问题——特别是没什么理论基础——的人来说,是非常困难的。因此,当我刚开始研究小波变换时,我花费了大量的时间才弄明白它究竟是怎么一回事。因此,我决定为不熟悉小波变换的人编写本教程。客观地讲,我并没有弄清楚所有的理论细节,但是,就工程应用而言,本教程应该会起到作用。 在本教程中,我将尝试给出小波理论所涉及的基本概念。由于本教程是面向工程实践的,因此不会给出定理和相关方程的证明。如果读者对它们感兴趣,可以自行作进一步的研究。 本篇作为系列教程的第一篇,假定读者没有任何背景知识——如果不是这样,那么可以选择跳过。 1、什么是变换?对于「什么是变换」这个问题,我想用两句古诗来启发读者:横看成岭侧成峰,远近高低各不同。山就在那里,观察者处在不同的位置进行观察后所得到的印象是不同的。如果想要得到山的全貌,那么就要变换不同的位置多次进行观察——这也解释了我们为什么需要变换。 首先,为什么我们需要变换?或者说,什么是变换? 作为信号处理中非常重要的概念,提及「变换」就不得不提及变换的对象:信号。为了更好地理解文章的内容,首先介绍一些必需的基本概念: 频率(frequency):一个事物在单位时间内变化的次数。“单位时间”一般是1秒,因此,频率的大小可以用“周期/秒”进行量化——它有一个更常用的名字:赫兹。例如,我们平时用的交流电是50Hz,就是说它的电流方向在1秒钟内变化了50次。 时域(time-domain)信号:将采集到的信号数值按照时间的流逝进行排列,就得到了时域信号。这是我们生活中最常见的信号表达形式,如股价的走势图、心电图、24h降水曲线图等。接着古诗中的描述,可以把这种表达形式作为「横看」。 频域(frequency-domain)信号:将采集到的信号按照其频率分布进行排列。在这种表达形式中,可以直观地得到信号的频率是怎样的。类似地,这种表达形式可以被视为「侧看」。 读者注意,所谓「时域信号」和「频域信号」,不是指时域中的信号和频域中的信号,而是指一个信号在时域中的表现和频域中的表现。但为了表述方便,仍采用上述方式。一个信号从产生的那一刻起,它就在时域和频域上都存在了。 下图分别展示了具有不同频率的正弦信号在时域上的波形图,其频率分别是3Hz、10Hz和50Hz: 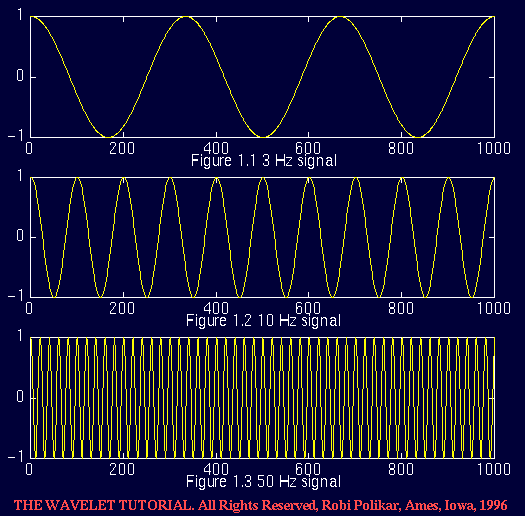 图1.1
图1.1
显然,频率越大,那么对应的信号变化得越快。 那么,给定两个频率未知的信号在时域上的波形图,我们如何比较其频率大小呢?如果它们的频率差距很大,当然可以通过观察时域信号的方式得出结论——但如果频率比较接近或者说想要得到它们的频率数值时,该怎么办呢?于是,问题就变成了:除了通过「观察」这种主观性非常强的方式,有没有一种量化手段可以帮助人们根据信号的时域信息客观地得到其频率信息? 答案是肯定的。大名鼎鼎的傅里叶变换(Fourier Transform,FT)就是解决这个问题的。具体来讲,对一个时域信号应用傅里叶变换,就会得到该信号在频域上的表示。 傅里叶变换就是一种改变观察者站位的手段,通过它,我们看山(信号)的角度从横看(时域)变成了侧看(频域)。 与信号在时域中的分布类似,我们也可以对信号的频域分布进行可视化:一个轴是频率值,一个轴是幅度。 频率轴的取值从0开始,直到正无穷大(频率最低为0,即信号不随时间发生变化)。对于每一个频率值,都对应一个幅度值。例如,如果对家用交流电的时域信号应用傅里叶变换并进行可视化,那么得到的频域图中将会在50Hz处出现一个尖峰,且其他频率的幅度都几乎为0。值得注意的是,在工程实践中,大多数信号都不会有这样简单的频域分布,它们往往是有多个频率混合而成的。 频率对应的幅度值,我并没有很好的理解,猜测与频率的持续时间以及构成原始信号的各个子正(余)弦信号的振幅有关。如果读者可以访问维基百科,可以参考一下这个动图。 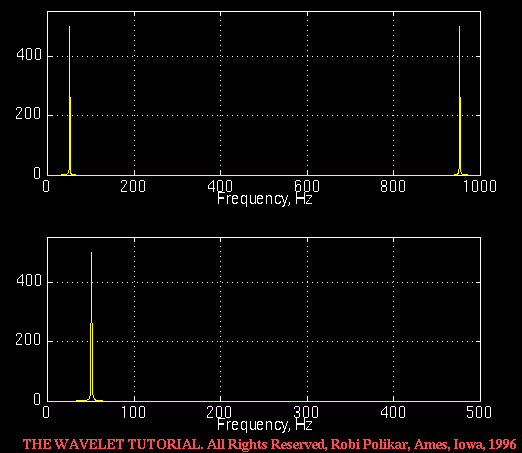 图1.2
图1.2
上图是家用交流电的频域信号可视化图,简称为频谱图,下半部分其实是对上半部分左侧图像的放大。出于某些对工程应用并不重要的原因,信号的频谱图总是对称的。因此,在本教程后面大部分有关傅里叶变换的频谱图中,我只展示对称的前一部分。 2、频率信息的作用及傅里叶变换的局限其实在第一章中已经提到,变换的目的是为了更全面地掌握信号中所蕴含的信息。在许多情况下,人们无法从时域信号中发现有用的信息时,将其转换到频域中则可能会带来很大帮助。 让我们举一个有关生物信号的例子。假设我们正在观察一个心电图信号,健康心电图信号的典型形状是心脏病专家所熟知的,与该形状的任何显著偏差通常会被认为是某种疾病症状。原始信号经传统心电图仪采集后只输出其时域信息,然而这种疾病的症状在时域中可能并不总是很明显,因此,新的计算机心电图分析仪也利用傅里叶变换并得到频率信息来帮助医生判定患者是否存在病理状况。 如今,傅里叶变换的应用可以说遍布工程领域的各个分支。尽管傅里叶变换名声很大,但它并不是唯一的选择。还有许多其他的变换也在工程实际和理论研究中取得了广泛的应用:希尔伯特变换(Hilbert Transform)、短时傅里叶变换(short-time Fourier Transform,后续篇目会进行介绍)、维格纳分布(Wigner Distributions)、Radon变换等,当然,还有我们将要介绍的小波变换(Wavelet Transform)。每一种变换都有其适用的领域及优缺点,小波变换也不例外。 为了更好地理解小波变换,我们需要进一步研究一下傅里叶变换。 傅里叶变换是一种可逆的变换,这就是说它可以将变换后的信号再复原回去。但是,对于傅里叶变换而言,在任何固定的时刻,仅有一种信息可供利用。具体而言,在时域信号的任何一个时刻(横轴上的一个点),无法得到信号在该点的频率信息;在频域信号的任何一个频率(横轴上的一个点),无法得到信号在该点对应的持续时间。那么有人可能就会问了:是否有必要同时得到一个信号的时域信息和频域信息呢? 这个问题的答案取决于具体的应用场景和信号的特性。回想一下,傅里叶变换可以告诉我们信号的频率信息,但是它仅仅告诉我们各频率的幅度,并没有告诉我们某个频率在时域信号中的起止时间;同样的,傅里叶变化并不能告诉我们时域分布中的信号在某一个时刻的频率是什么样的。 从频率的定义可以看出,单独的时刻是没有信号的变化的,因此也不可能只观察一个点就得到这个点的频率。 如果信号是平稳的,那么就不存在上述限制。 简而言之,如果一个信号的频率并不随着时间变化,那么这个信号就是平稳的。 平稳的性质在信号处理中有非常重要的地位。对于平稳信号而言,由于不存在频率的变化,所以在任意时刻,它的频率都是相同的。 但对于平稳信号而言,我们仍然没办法从时域中的一个点得到信号的频率,因为它在这个点是没有变化的。只是说这个信号本身的内在频率贯穿于其整个生命周期,以至于在任意时刻,它的频率都是相同的。 我们用如下方程来模拟一个平稳信号: x ( t ) = c o s ( 2 π ⋅ 10 t ) + c o s ( 2 π ⋅ 25 t ) + c o s ( 2 π ⋅ 50 t ) + c o s ( 2 π ⋅ 100 t ) x(t) = cos(2 \pi \cdot 10 t) + cos(2 \pi \cdot 25 t) + cos(2 \pi \cdot 50 t) + cos(2 \pi \cdot 100 t) x(t)=cos(2π⋅10t)+cos(2π⋅25t)+cos(2π⋅50t)+cos(2π⋅100t) 在任意时刻,它的频率都是10Hz、25Hz、50Hz和100Hz的叠加态。其时域分布图如下: 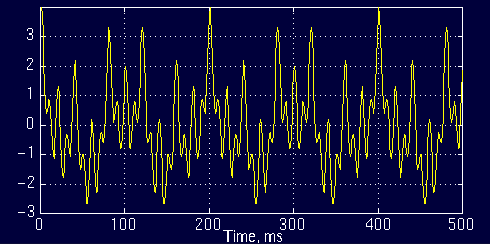 图1.3
图1.3
对其应用傅里叶变换,得到的频域分布图如下: 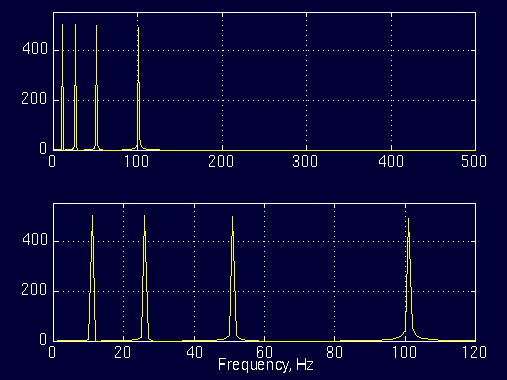 图1.4
图1.4
从图中可以看出,原始信号对应的频率共有四个值,分别是:10Hz、25Hz、50Hz和100Hz。 接着,我们构造如下一个频率随时间发生变化的不平稳的信号: 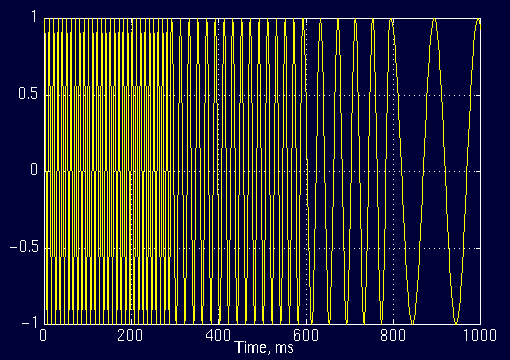 图1.5
图1.5
对于上图中的信号,在0到300ms中,频率为100Hz;在300ms到600ms中,频率为50Hz;在600ms到800ms中,频率为25Hz;在800ms到1000ms中,频率为10Hz。 经过傅里叶变换后,其频域分布图如下: 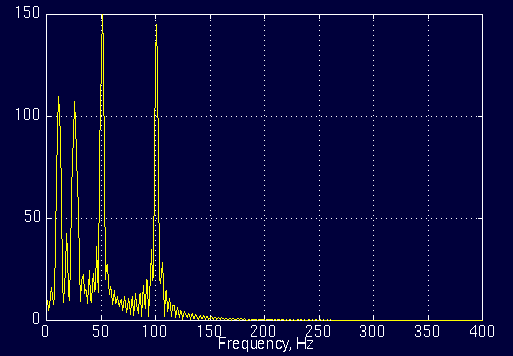 图1.6
图1.6
首先我们注意到,该信号在10Hz、25Hz、50Hz和100Hz处有较高的分量;其次,在坐标10Hz、25Hz、50Hz和100Hz周围有一些微小的幅度波动,这是由于时域信号中频率的突变导致的,我们暂且不去关注它们;另外,我们注意到,高频分量的幅度大于低频分量的幅度,这是由于高频信号持续的更长的时间(300ms vs 200ms)。 除去那些细小波动,频域分布图中的四个峰值正好与时域分布中信号的四种频率相对应,看上去似乎是这样的。实际上呢? 我们知道,对于图1.3中的信号而言,各个频率分量是在任意时刻是同时存在的。这也就是上面说的,一个平稳信号的频率是由频域分布中各个频率组合而成的,它们存在于信号的全生命周期中。 而图1.5中的信号的频率随时间发生了突变,其频域图中各个频谱分量在各自的时间段内单独存在,并没有存在于信号的全生命周期中。 对比两个信号的频谱图(图1.4和图1.6)可以发现,它们的相似性是显而易见的:它们都有四个频谱分量,且值对应相等。除去那些细小波动以及频率的幅度,这两个频域分布图几乎可以说是一致的,尽管它们对应的时域信号差别很大。那么,为什么两个完全不同的信号的频谱看起来非常相似呢?这是因为傅里叶变换只能给出信号的频谱内容(即信号中有哪些频率),但无法给出这些频率出现的时刻信息。因此,傅里叶变换不适用于非平稳信号,除非你只关心频率的值而不关心其存在的时间范围。 所以,当需要对信号的频率值在时间上进行定位时,我们需要一种新的变换手段。 3、可能的解决方案后面的文章详细介绍了小波变换的原理,本部分内容只是针对上述问题进行一些直觉上的思考以作为铺垫。 让我们重新思考一下上文提到的一个观点:从时域信号上的任一个时刻入手,是没办法知道该信号的频率的。原因也已经提到:在固定的时刻,信号无法发生变化,因此也就没有频率。 既然在固定的时刻无法获取信号的频率信息,那如果选择一个时间区间,通过观察该时间区间内的信号的取值情况,是否可以得到信号的频率呢?答案是肯定的。理论上来说,只要选择的时间区间内包含不止一个信号观察值,那么信号在该观察区间内就发生了变化——有变化,就可以计算频率了(尽管有可能频率为0)。 我认为「没有频率」和「频率为0」是两个不同的概念。前者是说没有频率产生的条件,后者是说信号在一定观察区间内没有变化。 上述思路提供了一种可能的解决方案:选择一个时间窗口对信号进行观察,如果该时间窗口足够小,那么就可以认为在该窗口内的子信号是近似平稳的,于是就可以对该子信号应用傅里叶变换并得到其频率表现。这样,我们就得到了在某个(非常小的)时间段内的信号的频率值! 读者很可能听过量子力学中的“测不准原理”,即:人们无法同时知道运动粒子的动量和位置。这其实与人们无法同时知道信号的时刻与频率非常类似。 尽管我们已经找到了一种可能的解决方案(实际上确实是短时傅里叶变换的做法),但我知道读者仍可能会有如下疑问:多小的时间区间叫做足够小?如果小区间内的信号不是平稳的该怎么办? 别急,解决这些问题是下一篇文章的事情。作为本文的结尾,我想再向读者介绍一下「分辨率」的概念。 这里的分辨率与通常理解的分辨率没什么两样,都是指对某种特性的区分程度的大小。对应于时域和频域,分别有「频率分辨率」「时间分辨率」: 频率分辨率:人们有多大把握能确定在特定时间段的信号的频率是准确的。时间分辨率:人们有多大把握能确定具有特定频率的信号的发生时间是准确的。举一个频率分辨率的例子来帮助理解:1000Hz的信号在1s内会变化1000次,而1Hz的信号只变化1次——在相同的时间范围内,前者变化了如此多的周期,以至于相较于后者,人们更有把握说对高频信号了解得更准确一些。 下一篇:第二篇:傅里叶变换与短时傅里叶变换 |
【本文地址】