excel统计分析

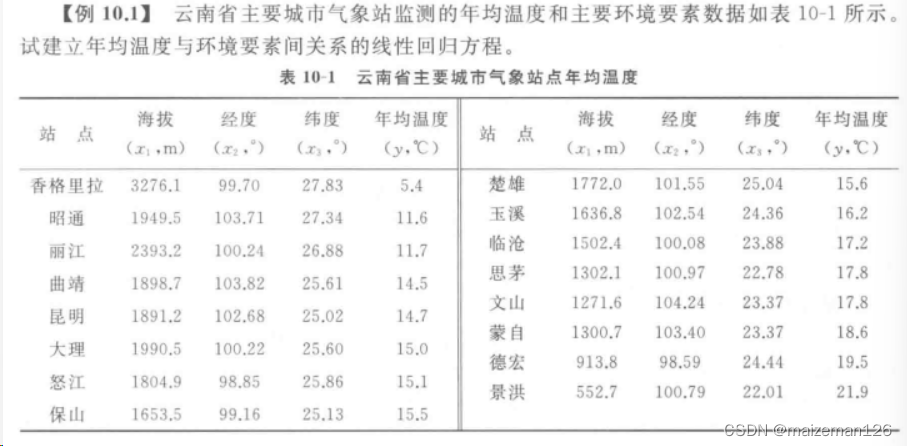
参考资料：生物统计学

        多元线性回归（multiple linear regression）是具有一个因变量或多个（两个或以上）自变量的线性回归，是直线回归的拓展，其模型和计算过程与直线回归类似，只是在计算上更为复杂。

1、回归方程建立

        设y是一个可观测的随机变量，收到m个非随机因素x1，x2，...，xm和随机因素的影响，如果y与x1，x2，...，xm间存在线性关系，则：

其中；α为截距；为其他因素固定不变时，因素变动一个单位是y变动的单位数，称为因素对y的偏回归系数（partial regression coefficient）；为随机误差，服从的正态分布，其中为离回归方差，其平方根为离回归标准差，又称回归估计标准误。

        用个体数据表示时，多元线性回归模型为：

        建立回归方程的过程，是求一组偏回归系数b1，b2，...，bm，使离回归平方和

最小化的过程。

        令，，，...，，则：

        根据最小二乘法的原理，要使Q有最小值，需b1，b2，...，bm的偏微分方程的值为0。将平方和记为，乘积和记为，记为，得方程组：

...       ....      ...      ...      ...      ....      ...      ....

案例如下：

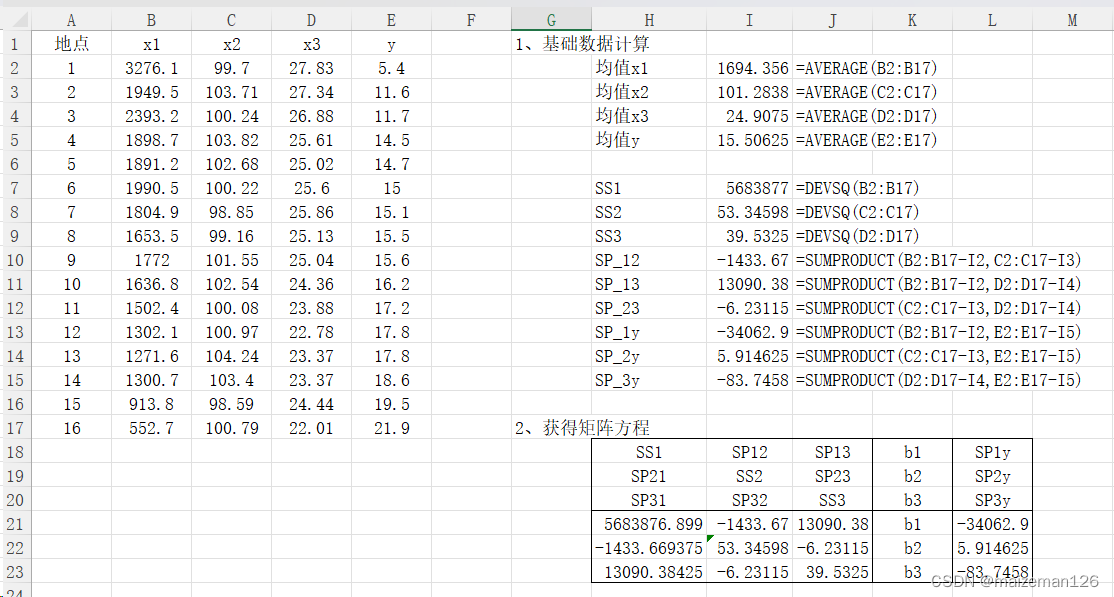
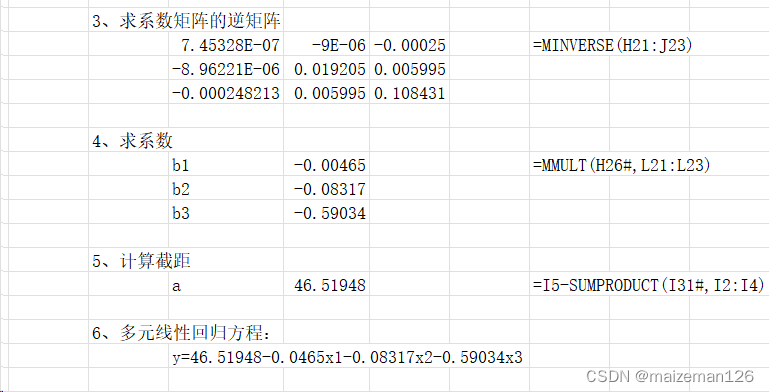
excel计算过程如下：

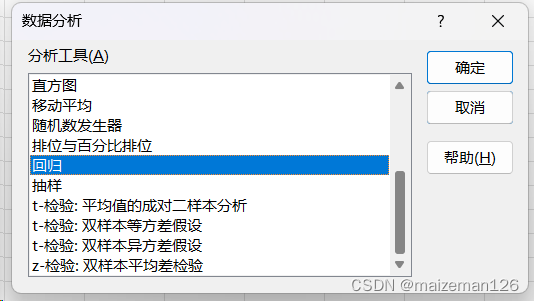
2、回归方程和偏回归系数检验

        和直线回归一样，建立的多元线性回归方程仍然需要进行显著性检验，达到显著水平的线性回归方程才有意义。

（1）回归方程的检验

        与直线回归类似，因变量y的总平方和（SSy）分解为回归平方和Uy和离回归平方和Qy两部分。回归平方和Uy为回归关系形成的部分，其自由度，根据定义：

离回归平方和Qy即实际观测值y和线性回归方程的估计值之间的差，为

        总自由度为，除去回归自由度，离回归自由度。

        零假设为：

        备择假设：不全为零。

        F统计量为：，服从df1=m，df2=n-m-1的F分布。

（2）偏回归系数的检验

        根据备择假设不全为零，并不是说均不为零，所以需逐个对进行检验，只有所有自变量的偏回归系数都达到显著水平时，回归方程才是最优回归方程。

        偏回归系数的显著性假设检验为：

        零假设：

        备择假设：

        具体可采用t检验或F检验进行检验。

        1）t检验

        偏回归系数b_i的标准误为：

 其中，s_y为因变量y的标准误，即；c_ii为建立线性回归方程时系数矩阵A的逆矩阵主对角线上对应自变量xi的元素。

        由于符合df=n-m-1的t分布，所以在假设时，根据

可检验bi来自总体的概率。

        2）F检验

        多元线性回归中，Uy总是随着m的增加而增大，增加自变量xi后增加的平方和Ui，称为y在xi上的偏回归平方和。计算公式为：

        由于增加变量xi后增加的自由度为1，所以

        也可以检验bi来自总体的概率。实际上t检验与F检验结果一致。

        对于偏回归系数的检验，t检验和F检验的寄过是完全一致的，选用其中之一即可。

excel操作如下：

①数据分析工具中选择“回归”

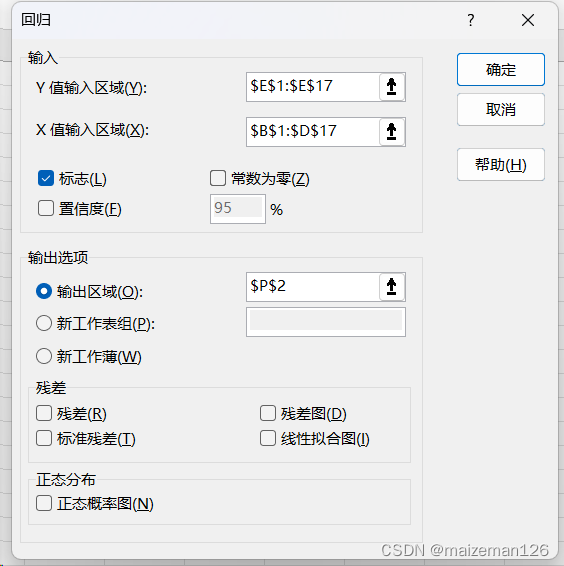
②在“回归”对话框中，录入输入与输出区域

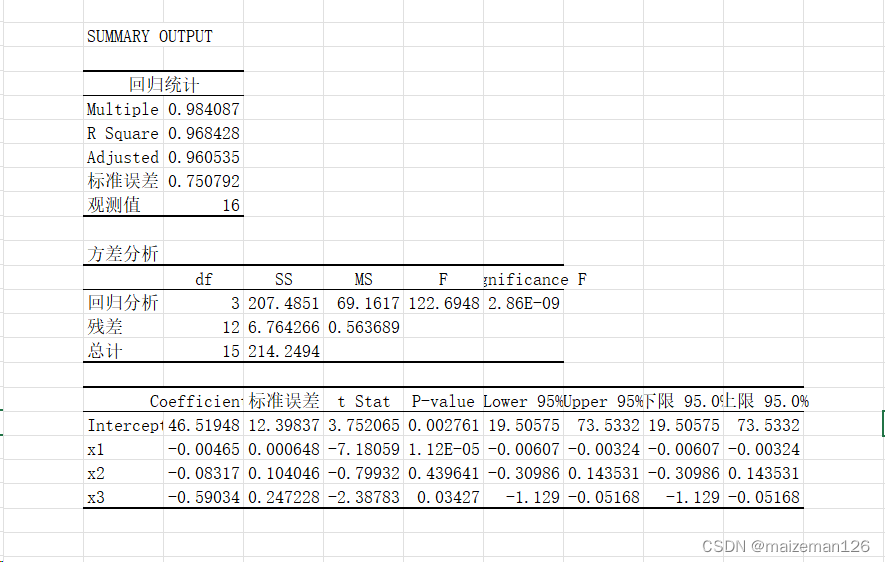
③输出结果

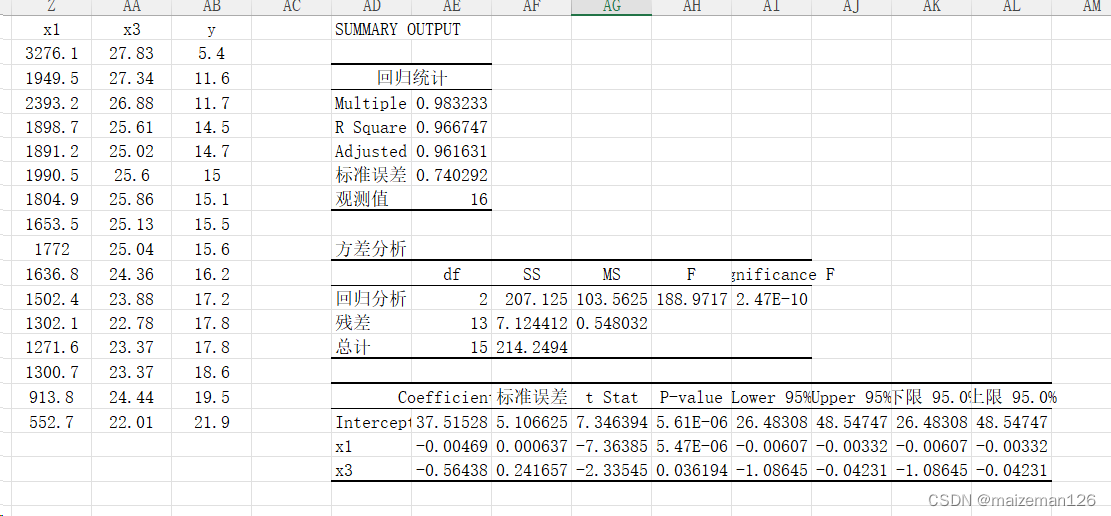
结果：x1和x3的偏回归系数达到显著水平，而x2的偏回归系数未达显著水平。

3、逐步回归

        在建立线性回归方程中，只要有一个因素的偏回归系数达到显著水平，根据回归平方的计算原理，线性回归方程总能达到显著水平。所以与直线回归不同，在多元线性回归中，偏回归系数的显著性与线性回归方程的显著性不同。

        由于线性回归方程中含有不显著的因素时，线性回归方程也可能显著，为使方程能正确表达变量间的关系，需要剔除线性回归方程中不显著的自变量，保证在线性回归方程中的自变量的偏回归系数均达到显著水平，这时的线性回归方程称为最优线性回归方程（optimal linear regression equation）。

        建立最优线性回归方程采用逐步回归（stepwise regression）方法。逐步回归分为逐步引入自变量和逐步剔除自变量两种方法。

（1）逐步引入自变量

        ①用每个自变量与因变量建立直线线性回归方程（或计算相关系数）并进行显著性检验。

        ②按回归系数（或相关性系数）的显著性顺序依次引入自变量建立线性回归方程并进行偏回归系数检验。

        ③直到引入自变量后该自变量的偏回归系数不显著为止。

（2）逐步剔除自变量

        ①用所有自变量与因变量建立线性回归方程并进行显著性检验。

        ②回归方程检验检验显著时，对偏回归系数进行显著性检验。

        ③存在不显著的偏回归系数时，从偏回归系数最不显著的自变量开始，每次剔除一个自变量。

        ④重新建立线性回归方程，直到方程中所有自变量的偏回归系数均显著位置。

        两种方法建立的最优线性方程可能不同。差异在于逐步引入自变量的方法使用的是单个变量回归系数，强调的自变量的单独作用；逐步剔除自变量的方法使用的是偏回归系数，强调自变量的综合作用。

本例中鉴于已进行了3个变量的显著性检验，故采用逐步剔除法，现将x2剔除，再次进行显著性检验，步骤同上一步一样。结果如下：

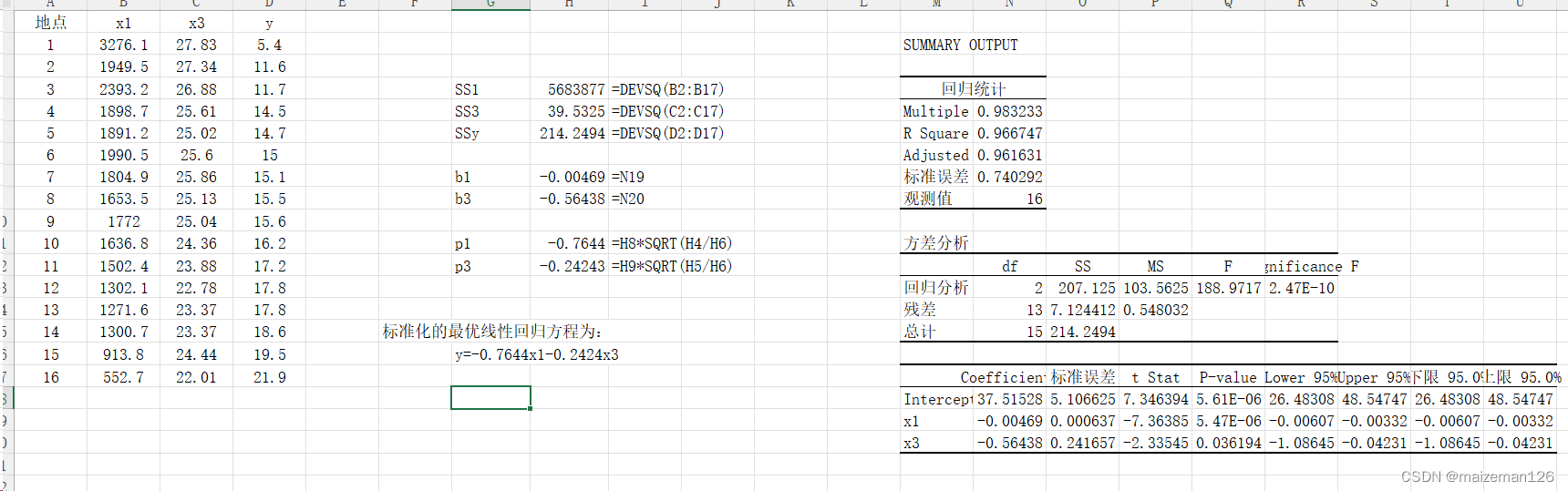
结果显示：x1和x3的偏回归系数仍然达到显著水平，故其最优线性回归方程为：

4、通径分析

        由于偏回归系数带有单位，所以不能通过比较偏回归系数的大小来比较自变量对因变量相对影响的大小。为判断自变量对因变量相对影响的大小，需对偏回归系数进行标准化处理，去除单位后，用标准化的偏回归系数来进行比较。标准化后的偏回归系数称为通径系数（path coefficient），记为，表示自变量对因变量y的直接影响程度。

        通径系数定义为：偏回归系数与变量标准差比的乘积。即

        令，，得标准化的回归方程：

        由于标准化的回归方程为原回归方程的变形，所以标准化的回归方程与原多元线性回归方程的显著性一致；同理，通径系数为偏回归系数的变形，通径系数与偏回归系数的显著性水平一致。

通径分析的结果可知：变量x1对y的影响较变量x3的影响更大。