对勾型函数

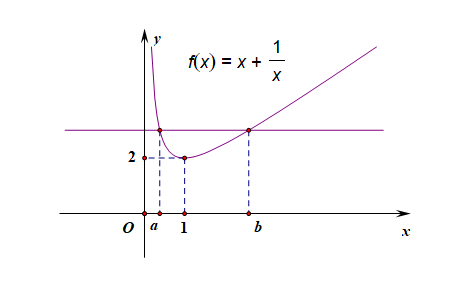
对勾函数是一种类似于反比例函数的一般双曲函数，是形如 \(f(x)=ax+\cfrac{b}{x}\) (\(ab>0\)) 的函数，由于其图像样子像对勾 \(\checkmark\) ，所以好多人形象的称其为“对勾函数”，又或称其为“耐克函数”。也被称为“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。对勾函数中的特殊例子， \(f(x)=x+\cfrac{1}{x}\) 是高中数学中的一个非常特殊且高频考查的函数，

用导数法判断函数\(f(x)=x+\cfrac{1}{x}\)的单调性并求其值域。

分析：函数的定义域是\(x\in(-\infty，0)\cup(0，+\infty)\)，且是奇函数，

故只先研究\(x\in(0，+\infty)\)上的图像，研究工具是导数。[1]

先求导，得到\(f'(x)=1-\cfrac{1}{x^2}=\cfrac{x^2-1}{x^2}\)，

令\(f'(x)>0\)，即\(x^2-1>0\)，得到\(x>1\)；

令\(f'(x)0\)时，函数\(g(x)=x+\cfrac{1}{x}\)有最小值\(g(x)_{min}=g(1)=2\)，

而由\(g(x)=x+\cfrac{1}{x}\geqslant 2\sqrt{x\cdot \cfrac{1}{x}}=2\)，(当且仅当\(x=\cfrac{1}{x}\)，即\(x=1\)时取等号)

其实均值不等式的使用就是对勾函数在其极值点处的具体应用；理解了这一点，我们就有以下的收获：

①函数图像拐弯的点的坐标的快速记忆方法[抽象为更一般的情形，比如\(m(x)=ax+\cfrac{b}{x}(a>0，b>0)\)]，

横坐标令\(ax=\cfrac{b}{x}\)，则得到\(x=\sqrt{\cfrac{b}{a}}\)，纵坐标令\(ax+\cfrac{b}{x}\geqslant 2\sqrt{ab}\)，

故在第一象限的那个特殊点的坐标为\((\sqrt{\cfrac{b}{a}}，2\sqrt{ab})\)，在第三象限的那个特殊点的坐标为\((-\sqrt{\cfrac{b}{a}}，-2\sqrt{ab})\)；

②如果均值不等式失效，则自然应该联想到使用对勾型函数求最值；

比如求 \(g(x)=x+\cfrac{2}{x}(x\geqslant 2)\)的最小值，

当你使用均值不等式[能看到已满足正定]时，得到 \(g(x)=x+\cfrac{2}{x}\geqslant 2\sqrt{2}\)，形式上有了最小值 \(2\sqrt{2}\)，当且仅当\(x=\cfrac{2}{x}\)，即 \(x=\sqrt{2}\) 时才能取到等号；但是这是错误的，原因是等号在自变量的取值集合(定义域) \(\{x\mid x\geqslant 2\}\)内取不到。此时我们利用其单调性，可知其在\([2，+\infty)\)上单调递增，故\(g(x)_{min}=g(2)=2+\cfrac{2}{2}=3\)。

②分子二次分母一次型，如\(h(x)=\cfrac{x^2-4x+5}{x-2}\)，

如[配凑法]\(h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}\)，

或[换元法]令\(x-2=t\)，则\(x=t+2\)，

故\(h(x)=\cfrac{(t+2)^2-4(t+2)+5}{t}=\cfrac{t^2+1}{t}=t+\cfrac{1}{t}\)

即\(h(x)=t+\cfrac{1}{t}=(x-2)+\cfrac{1}{x-2}\)

\(f(x)=\cfrac{9^x+1}{3^x}=\cfrac{(3^x)^2+1}{3^x}=3^x+3^{-x}\)，或\(\stackrel{3^x=t}{\Longrightarrow}f(x)=\cfrac{t^2+1}{t}=t+\cfrac{1}{t}\)

③分子一次分母二次型，如\(n(x)=\cfrac{x+1}{x^2+3x+3}\)；

如\(n(x)=\cfrac{x+1}{x^2+3x+3}\)；则\(n(x)=\cfrac{x+1}{(x+1)^2+(x+1)+1}=\cfrac{1}{(x+1)+\cfrac{1}{x+1}+1}\)

如\(g(t)=\cfrac{t}{t^2+9}=\cfrac{1}{t+\frac{9}{t}}\)；如\(h(t)=\cfrac{t+2}{t^2}=\cfrac{1}{t}+2(\cfrac{1}{t})^2=2m^2+m\);

或经过分离参数，得到分式型函数，

对一切实数\(x\)，不等式\(x^2+a|x|+1\geqslant 0\)恒成立，则实数\(a\)的取值范围是______________.

分析：当\(x=0\)时，原式为\(1\geqslant 0\)恒成立，则\(a\in \R\);

当\(x\neq 0\)时，原式可化为\(a|x|\geqslant -(x^2+1)\)，即\(a\geqslant -(|x|+\cfrac{1}{|x|})\)恒成立；

又由于\(|x|+\cfrac{1}{|x|}\geqslant 2\)，则\(-(|x|+\cfrac{1}{|x|})\leqslant -2\)

故有\(a\geqslant -2\)，

综上所述，两种情形求其交集，可得\(a\)的取值范團是\([-2， +\infty)\);

对勾型+奇函数：

对勾型+偶函数：

非对勾型+奇函数：

非对勾型+偶函数：

【数学常识储备】已知函数\(f(x)=x+\cfrac{1}{x}\)，若互异的实数\(a\)，\(b\)满足方程\(f(a)=f(b)\)，则\(ab=1\)。

分析：由\(f(a)=f(b)\)，可知 \(a+\cfrac{1}{a}=b+\cfrac{1}{b}\)，对此变形整理，得到：

\((a-b)(1-\cfrac{1}{ab})=0\)，由于 \(a-b\neq0\)，故 \(1-\cfrac{1}{ab}=0\)，则\(ab=1\).

引申：【2022届高三数学三轮模拟冲刺用题】已知 \(f(x)=x+\cfrac{1}{x}\) ，若 \(f(a)=f(b)\) 且 \(b>a>0\)，试求解 \(\cfrac{1}{a}+\cfrac{2}{b}\) 的最小值，则可以这样求解如下，

由上述储备知识可知，\(0