| 《神经网络与深度学习》 矩阵微积分 | 您所在的位置:网站首页 › 对q求导 › 《神经网络与深度学习》 矩阵微积分 |
《神经网络与深度学习》 矩阵微积分
|
1. 有限元中涉及的矩阵微分
(虽然科目不同,但涉及内容相同,顺带着一起说了) k矩阵 -------------------------------------------- P为列向量 trans(P)*q对trans(q)求导 结果为trans(P) 所以有限元中 trans(q)kq/2 - trans(P)q对q求导,结果为trans(q)*k - P 至于为什么有限元书上结果为 kq - P,那是因为单元刚度矩阵为对称矩阵 2.复习矩阵论微积分(1) 矩阵求导,对每个元素求导 dA/dt (2) 矩阵求积分,对每个元素求积分 ∫Adt (3) 矩阵函数对矩阵求导 df(X)/dX,函数对每个矩阵元素求导 (4) 向量函数对向量求导 df(x)/dx,函数对每个向量元素求导 注:向量为列向量,求导后的向量也为列向量。 注:向量函数、矩阵函数是一个标量函数 举例: tr(X)就是一个矩阵函数 trans(x)*a就是一个向量矩阵 x与a为列向量
(5) 矩阵值函数对矩阵求导 d(AX)/dX d(trans(x)A)/dx x为列向量 trans(x)A 1x3维 如f11=x1*a11+x2*a21+x3*a31 f11对x的每个元素求导 结果为3x1维 同理fij对x的每个元素求导 最终结果为3x3维矩阵 矩阵论里面也就这么点内容 3. 《神经网络与深度学习》附录 矩阵微积分分子布局与分母布局区别:对向量求导后是写成列向量还是行向量? 我之前认为对列向量求导,那么结果写成列向量,对行向量求导,结果写成行向量。 向量函数对向量求导 df(x)/dx 分母布局,结果为列向量,分子布局,结果为行向量 向量求导 dx/dt 分母布局,结果为行向量,分子布局,结果为列向量 向量值函数对向量求导,结果称为雅可比矩阵 如d(trans(x)A)/dx 复合函数的计算法则 链式法则 y为关于变量x的s维向量,z为关于向量y的t维向量 注:上下文的向量都为列向量。求导结果都为分母布局
softmax函数求导 如x为3维向量 z1 = softmax(x1) = exp(x1)/[exp(x1)+exp(x2)+exp(x3)] z2 = softmax(x2) = exp(x2)/[exp(x1)+exp(x2)+exp(x3)] z3 = softmax(x3) = exp(x3)/[exp(x1)+exp(x2)+exp(x3)] z = [exp(x1) exp(x2) exp(x3)]/[exp(x1)+exp(x2)+exp(x3)] dz/dx 结果如下 书上的推导使用了公式 补充: 按位计算 如按之前的举例,d(trans(x)A)/dx,结果为一个3x3矩阵 如果是按位计算的话,结果为一个3x3对角矩阵 diag(d(trans(x)A)/dx1,d(trans(x)A)/dx2,d(trans(x)A)/dx3) hadamard积 kronecker积 向量外积 |
【本文地址】
 q为列向量
q为列向量 而该结果就是trans(q)*k 同理,trans(q)kq/2对qT求导 结果为一个行向量 而结果就是k*trans(q)
而该结果就是trans(q)*k 同理,trans(q)kq/2对qT求导 结果为一个行向量 而结果就是k*trans(q) trans(P)*q = P1u1+P2u2+P3u3 trans(P)*q对q求导,即trans(P)*q对q的每个元素求导 结果就是P
trans(P)*q = P1u1+P2u2+P3u3 trans(P)*q对q求导,即trans(P)*q对q的每个元素求导 结果就是P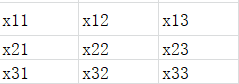 X为3x3
X为3x3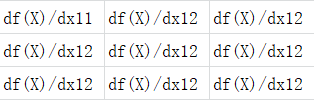 df(X)/dX为3x3
df(X)/dX为3x3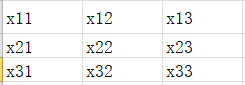 X矩阵
X矩阵 A矩阵
A矩阵 AX,如 f11=a11*x11 + a12*x21 + a13*x31 f11对X矩阵的每个元素求导 结果3x3维 共9个fij,所以最终矩阵大小为81维 下图 我只写出了分块矩阵的第一行的前两个元素
AX,如 f11=a11*x11 + a12*x21 + a13*x31 f11对X矩阵的每个元素求导 结果3x3维 共9个fij,所以最终矩阵大小为81维 下图 我只写出了分块矩阵的第一行的前两个元素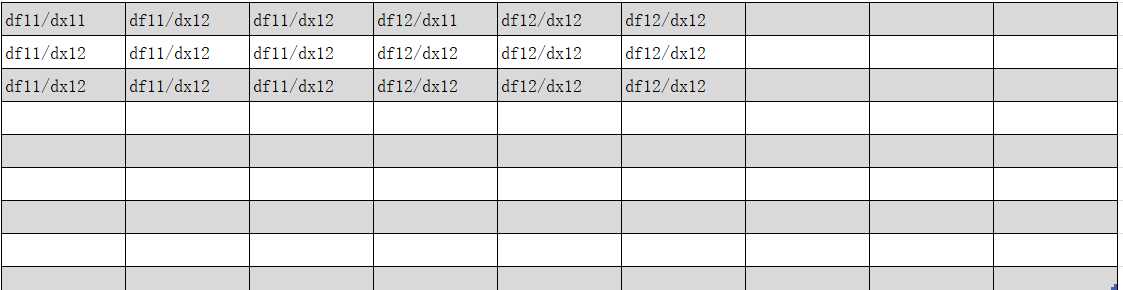 (6) 向量值函数对向量求导 d(Ax)/dx A矩阵 3x3维 x向量 3x1维 | Ax 3x1维 如f11=a11*x1+a12*x2+a13*x3 f11对x的每个元素求导 结果为3x1维 同理fij对x的每个元素求导 结果为9维列向量
(6) 向量值函数对向量求导 d(Ax)/dx A矩阵 3x3维 x向量 3x1维 | Ax 3x1维 如f11=a11*x1+a12*x2+a13*x3 f11对x的每个元素求导 结果为3x1维 同理fij对x的每个元素求导 结果为9维列向量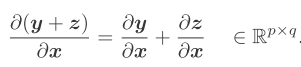 y z为q维向量,x为p维向量,结果为pxq矩阵
y z为q维向量,x为p维向量,结果为pxq矩阵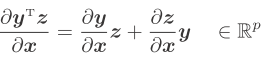 y z为q维向量,x为p维向量 结果为p维向量
y z为q维向量,x为p维向量 结果为p维向量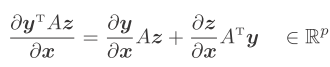 y为p维向量,z为q维向量,A为pxq 且与x无关 即相对于x来说 A为一个常数矩阵
y为p维向量,z为q维向量,A为pxq 且与x无关 即相对于x来说 A为一个常数矩阵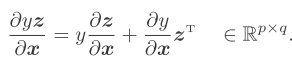 y为标量函数,z为q维,x为p维,结果pxq维矩阵
y为标量函数,z为q维,x为p维,结果pxq维矩阵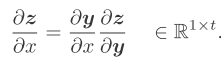 x为p维向量,y为关于向量x的s维向量,z为关于向量y的t维向量
x为p维向量,y为关于向量x的s维向量,z为关于向量y的t维向量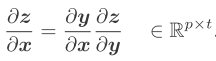 X为pxq维矩阵,y为关于矩阵X的s维向量,z为关于向量y的标量函数
X为pxq维矩阵,y为关于矩阵X的s维向量,z为关于向量y的标量函数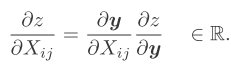
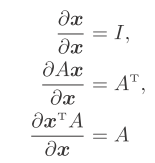 标准逻辑函数求导
标准逻辑函数求导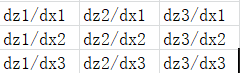
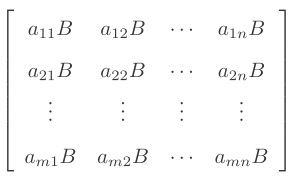 矩阵维数很大
矩阵维数很大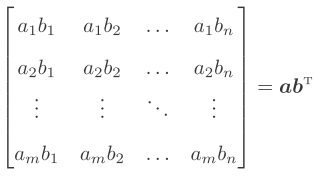 也就是并积
也就是并积