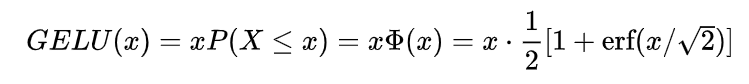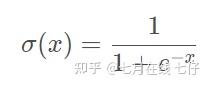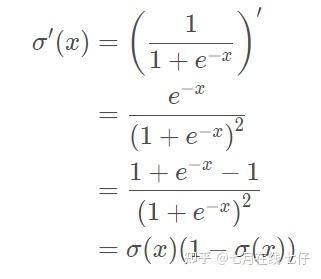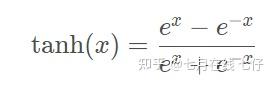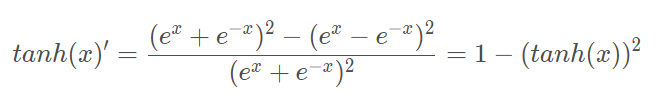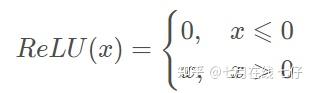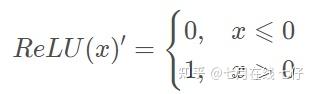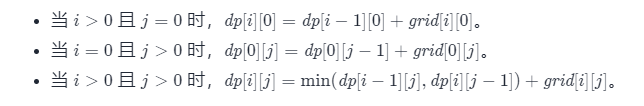2021年9月底

QK进行点击之后，值之间的方差会较大，也就是大小差距会较大；如果直接通过Softmax操作，会导致大的更大，小的更小；进行缩放，会使参数更平滑，训练效果更好。

多次attention综合的结果至少能够起到增强模型的作用，也可以类比CNN中同时使用多个卷积核的作用，直观上讲，多头的注意力有助于网络捕捉到更丰富的特征/信息。

BPE与Wordpiece都是首先初始化一个小词表，再根据一定准则将不同的子词合并。词表由小变大

BPE与Wordpiece的最大区别在于，如何选择两个子词进行合并：BPE选择频数最高的相邻子词合并，而WordPiece选择能够提升语言模型概率最大的相邻子词加入词表。

从bert最开始的mask token 到后面ernie的 mask entity以及还有mask n-gram，动态mask等等。

GELU函数是RELU的变种，形式如下：

常见的激活函数有：Sigmoid、Tanh、ReLU

Sigmoid函数：

求导：

特点：

它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1。

缺点：

缺点1：在深度神经网络中梯度反向传递时导致梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。

缺点2：Sigmoid 的 output不是0均值（即zero-centered）。

缺点3：其解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。

Tanh函数：

求导：

特点：它解决了Sigmoid函数的不是zero-centered输出问题，收敛速度比sigmoid要快，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

ReLU函数：

求导：

特点：

1.ReLu函数是利用阈值来进行因变量的输出，因此其计算复杂度会比剩下两个函数低（后两个函数都是进行指数运算）

2.ReLu函数的非饱和性可以有效地解决梯度消失的问题，提供相对宽的激活边界。

3.ReLU的单侧抑制提供了网络的稀疏表达能力。

该题为leetcode第64题

思路：动态规划

由于路径的方向只能是向下或向右，因此网格的第一行的每个元素只能从左上角元素开始向右移动到达，网格的第一列的每个元素只能从左上角元素开始向下移动到达，此时的路径是唯一的，因此每个元素对应的最小路径和即为对应的路径上的数字总和。

对于不在第一行和第一列的元素，可以从其上方相邻元素向下移动一步到达，或者从其左方相邻元素向右移动一步到达，元素对应的最小路径和等于其上方相邻元素与其左方相邻元素两者对应的最小路径和中的最小值加上当前元素的值。由于每个元素对应的最小路径和与其相邻元素对应的最小路径和有关，因此可以使用动态规划求解。

创建二维数组dp，与原始网格的大小相同，dp[i][j] 表示从左上角出发到 (i,j)位置的最小路径和。显然，dp[0][0]=grid[0][0]。对于dp 中的其余元素，通过以下状态转移方程计算元素值。

代码如下：

时间复杂度：O(mn)

空间复杂度：O(mn)

思路：回溯算法

使用回溯算法框架即可，先考虑一位的情况，然后把递归地考虑去掉这一位数后的数组的全排列。

代码如下：

时间复杂度：O(n×n!)

空间复杂度：O(n)