| 逆Wishart分布在贝叶斯推理中的应用 | 您所在的位置:网站首页 › 多元正态概率密度函数 › 逆Wishart分布在贝叶斯推理中的应用 |
逆Wishart分布在贝叶斯推理中的应用
|
Wishart分布的概率密度函数
f ( w ∣ v , H ) = ∣ w ∣ ( v − p − 1 ) / 2 2 v p / 2 Γ p ( v / 2 ) ∣ H ∣ v / 2 e x p [ − 1 2 t r ( H − 1 w ) ] 其 中 , Γ p ( v / 2 ) = π p ( p − 1 ) / 4 ∏ j = 1 p Γ ( v + 1 − j 2 ) f(w|v,H) = {|w|^{(v-p-1)/2} \over 2^{vp/2} \Gamma_{p}(v/2)|H|^{v/2}}exp[-{1 \over 2}tr(H^{-1}w)] \\ 其中, \Gamma_{p}(v/2) = \pi^{p(p-1)/4}\prod_{j=1}^{p}\Gamma({v+1-j \over 2}) f(w∣v,H)=2vp/2Γp(v/2)∣H∣v/2∣w∣(v−p−1)/2exp[−21tr(H−1w)]其中,Γp(v/2)=πp(p−1)/4j=1∏pΓ(2v+1−j) 在上式中, w w w是一个 p ∗ p p*p p∗p的随机矩阵, H H H是一个 p ∗ p p*p p∗p的特定矩阵, v v v表示自由度。也记作 W ( v , H ) W(v,H) W(v,H) 逆Wishart分布的概率密度函数f ( w ∣ v , H ) = ∣ H ∣ v / 2 2 v p / 2 Γ p ( v / 2 ) ∣ w ∣ ( v + p + 1 ) / 2 e x p [ − 1 2 t r ( w − 1 H ) ] f(w|v,H)= {|H|^{v/2} \over 2^{vp/2} \Gamma_{p}(v/2)|w|^{(v+p+1)/2}}exp[-{1 \over 2}tr(w^{-1}H)] f(w∣v,H)=2vp/2Γp(v/2)∣w∣(v+p+1)/2∣H∣v/2exp[−21tr(w−1H)] 在上式中, w w w是一个 p ∗ p p*p p∗p的随机矩阵, H H H是一个 p ∗ p p*p p∗p的特定矩阵, v v v表示自由度。也记作 I W ( v , H ) IW(v,H) IW(v,H) 多元正态分布的概率密度函数f ( X ∣ μ , Σ ) = 1 ( 2 π ) p / 2 ∣ Σ ∣ 1 / 2 e x p [ − 1 2 ( X − μ ) T Σ − 1 ( X − μ ) ] f(X|\mu, \Sigma) = {1 \over (2\pi)^{p/2} |\Sigma|^{1/2}}exp[-{1 \over 2}(X-\mu)^{T}\Sigma^{-1}(X-\mu)] f(X∣μ,Σ)=(2π)p/2∣Σ∣1/21exp[−21(X−μ)TΣ−1(X−μ)] X X X是一个 p p p维的向量。也记作 N ( μ , Σ ) N(\mu, \Sigma) N(μ,Σ) 正态-逆Wishart分布多元正态分布与逆Wishart分布的概率密度函数的乘积就是正态-逆Wishart分布的概率密度函数。 正态-逆Wishart分布的共轭分布还是正态-逆Wishart分布。 N I W = ∣ H ∣ v / 2 2 ( v p + p ) / 2 Γ p ( v / 2 ) ∣ w ∣ ( v + p + 1 ) / 2 1 π p / 2 ∣ Σ ∣ 1 / 2 e x p [ − 1 2 t r ( w − 1 H ) − 1 2 ( X − μ ) T Σ − 1 ( X − μ ) ] NIW = {|H|^{v/2} \over 2^{(vp+p)/2} \Gamma_{p}(v/2)|w|^{(v+p+1)/2}}{1 \over \pi^{p/2} |\Sigma|^{1/2}}exp[-{1 \over 2}tr(w^{-1}H)-{ 1 \over 2}(X-\mu)^{T}\Sigma^{-1}(X-\mu)] NIW=2(vp+p)/2Γp(v/2)∣w∣(v+p+1)/2∣H∣v/2πp/2∣Σ∣1/21exp[−21tr(w−1H)−21(X−μ)TΣ−1(X−μ)] 参数是 μ , Σ , v , H \mu, \Sigma, v, H μ,Σ,v,H 多元t分布t v ( x ∣ μ , Σ ) = Γ ( v / 2 + d / 2 ) Γ ( v / 2 ) ∣ Σ ∣ − 1 / 2 ( v π ) d / 2 [ 1 + 1 v ( x − μ ) T Σ − 1 ( x − μ ) ] − ( v + d ) 2 t_{v}(x|\mu, \Sigma) = { \Gamma(v/2 + d/2) \over \Gamma(v/2)}{|\Sigma|^{-1/2} \over (v\pi)^{d/2}} [1 + {1 \over v}(x-\mu)^{T}\Sigma^{-1}(x-\mu)]^{-(v+d) \over 2} tv(x∣μ,Σ)=Γ(v/2)Γ(v/2+d/2)(vπ)d/2∣Σ∣−1/2[1+v1(x−μ)TΣ−1(x−μ)]2−(v+d) x x x是一个 d d d维的向量, v v v是自由度, μ 和 Σ \mu和\Sigma μ和Σ是均值和方差。 后验分布假设有总体 A 1 , A 2 , , , A G A_{1}, A_{2},,, A_{G} A1,A2,,,AG,其中每一个总体 A i A_{i} Ai都服从 p p p维的正态分布,即有: A i ∽ N p ( μ i , Σ i ) A_{i} \backsim N_{p}(\mu_{i}, \Sigma_{i}) Ai∽Np(μi,Σi) 那么对于其中的某个总体 A i A_{i} Ai来说,如果在其中取 n i n_{i} ni个样本 X i , 1 , X i , 2 , X i , 2 , , , X i , n i X_{i,1}, X_{i,2}, X_{i,2},,, X_{i,n_{i}} Xi,1,Xi,2,Xi,2,,,Xi,ni,其样本统计量: X i ˉ = 1 n i ∑ j = 1 n i X i , j = f 1 ( X i ˉ ∣ μ i , Σ i ; A i ) V i = ∑ j = 1 n i ( X i , j − X i ˉ ) ( X i , j − X i ˉ ) T = f 2 ( V i ∣ μ i , Σ i ; A i ) \bar{X_{i}} = {1 \over n_{i}}\sum_{j=1}^{n_{i}}X_{i,j} = f_{1}(\bar{X_{i}}|\mu_{i}, \Sigma_{i};A_{i}) \\ V_{i} = \sum_{j=1}^{ n_{i}}(X_{i,j}-\bar{X_{i}})(X_{i,j}-\bar{X_{i}})^{T} = f_{2}(V_{i}|\mu_{i}, \Sigma_{i};A_{i}) Xiˉ=ni1j=1∑niXi,j=f1(Xiˉ∣μi,Σi;Ai)Vi=j=1∑ni(Xi,j−Xiˉ)(Xi,j−Xiˉ)T=f2(Vi∣μi,Σi;Ai) 统计量 X i ˉ , V i \bar{X_{i}},V_{i} Xiˉ,Vi二者相互独立 ,通过威沙特分布和逆威沙特分布可以知道, X i ˉ ∽ N p ( μ i , Σ i n i ) V i ∽ W p ( n i − 1 , Σ i ) \bar{X_{i}} \backsim N_{p}(\mu_{i}, {\Sigma_{i} \over n_{i}}) \\ V_{i} \backsim W_{p}( n_{i}-1, \Sigma_{i}) Xiˉ∽Np(μi,niΣi)Vi∽Wp(ni−1,Σi) 所以 f 1 ( X i ˉ ∣ μ i , Σ i ; A i ) f_{1}(\bar{X_{i}}|\mu_{i}, \Sigma_{i};A_{i}) f1(Xiˉ∣μi,Σi;Ai)的概率密度函数为: f 1 ( X i ˉ ∣ μ i , Σ i ; A i ) = N p ( μ i , Σ i n i ) = n i 1 / 2 ( 2 π ) p / 2 ∣ Σ i ∣ 1 / 2 e x p [ − n i 2 ( X i ˉ − μ i ) T Σ i − 1 ( X i ˉ − μ i ) ] \begin{aligned} f_{1}(\bar{X_{i}}|\mu_{i}, \Sigma_{i};A_{i}) = & N_{p}(\mu_{i}, {\Sigma_{i} \over n_{i}}) \\ = & {n_{i}^{1/2} \over (2\pi)^{p/2}|\Sigma_{i}|^{1/2}}exp[-{n_{i} \over 2}(\bar{X_{i}}-\mu_{i})^{T}\Sigma_{i}^{-1}(\bar{X_{i}}-\mu_{i})] \end{aligned} f1(Xiˉ∣μi,Σi;Ai)==Np(μi,niΣi)(2π)p/2∣Σi∣1/2ni1/2exp[−2ni(Xiˉ−μi)TΣi−1(Xiˉ−μi)] f 2 ( V i ∣ μ i , Σ i ; A i ) f_{2}(V_{i}|\mu_{i}, \Sigma_{i};A_{i}) f2(Vi∣μi,Σi;Ai)的概率密度函数为: f 2 ( V i ∣ μ i , Σ i ; A i ) = W p ( n i − 1 , Σ i ) = k i ∣ V i ∣ ( n i − p − 2 ) / 2 ∣ Σ i ∣ ( n i − 1 ) / 2 e x p [ − 1 2 t r ( Σ i − 1 V i ) ] 其 中 , k i = [ 2 ( n i − 1 ) p / 2 π p ( p − 1 ) / 4 ∏ j = 1 p Γ ( n i − j 2 ) ] − 1 \begin{aligned} f_{2}(V_{i}|\mu_{i}, \Sigma_{i};A_{i}) = & W_{p}( n_{i}-1, \Sigma_{i})\\ = & k_{i} {|V_{i}|^{(n_{i}-p-2)/2} \over |\Sigma_{i}|^{(n_{i}-1)/2}}exp[-{1 \over 2}tr(\Sigma_{i}^{-1}V_{i})] \\ & 其中,k_{i} = [2^{(n_{i}-1)p/2}\pi^{p(p-1) /4}\prod_{j=1}^{p}\Gamma({n_{i}-j \over 2})]^{-1} \end{aligned} f2(Vi∣μi,Σi;Ai)==Wp(ni−1,Σi)ki∣Σi∣(ni−1)/2∣Vi∣(ni−p−2)/2exp[−21tr(Σi−1Vi)]其中,ki=[2(ni−1)p/2πp(p−1)/4j=1∏pΓ(2ni−j)]−1 由于 X i ˉ , V i \bar{X_{i}},V_{i} Xiˉ,Vi二者相互独立,所以它们的联合概率分布的概率密度函数等于二者的乘积,所以样本的似然函数为: L ( X i ˉ , V i ∣ μ i , Σ i ) = f 1 ( X i ˉ ∣ μ i , Σ i ; A i ) f 2 ( V i ∣ μ i , Σ i ; A i ) = k i n i 1 / 2 ∣ V i ∣ ( n i − p − 2 ) / 2 ( 2 π ) p / 2 ∣ Σ i ∣ n i / 2 e x p [ − n i 2 ( X i ˉ − μ i ) T Σ i − 1 ( X i ˉ − μ i ) − 1 2 t r ( Σ i − 1 V i ) ] \begin{aligned} L(\bar{X_{i}}, V_{i}|\mu_{i}, \Sigma_{i}) = & f_{1}(\bar{X_{i}}|\mu_{i}, \Sigma_{i};A_{i})f_{2}(V_{i}|\mu_{i}, \Sigma_{i};A_{i}) \\ = & {k_{i}n_{i}^{1/2} |V_{i}|^{(n_{i}-p-2)/2}\over (2\pi)^{p/2}|\Sigma_{i}|^{n_{i}/2}}exp[-{n_{i} \over 2}(\bar{X_{i}}-\mu_{i})^{T}\Sigma_{i}^{-1}(\bar{X_{i}}-\mu_{i})-{1 \over 2}tr(\Sigma_{i}^{-1}V_{i})] \end{aligned} L(Xiˉ,Vi∣μi,Σi)==f1(Xiˉ∣μi,Σi;Ai)f2(Vi∣μi,Σi;Ai)(2π)p/2∣Σi∣ni/2kini1/2∣Vi∣(ni−p−2)/2exp[−2ni(Xiˉ−μi)TΣi−1(Xiˉ−μi)−21tr(Σi−1Vi)] 可以看出,似然函数的分布与正态-逆Wishart分布具有相同的形式,这样,由于正态-逆Wishart分布的共轭分布仍然是正态-逆Wishart分布,因此,可以选取如下形式的正态-逆Wishart分布作为参数 μ i , Σ i \mu_{i}, \Sigma_{i} μi,Σi的先验分布。 Σ i ∽ I W p ( v 0 , Λ 0 ) = k i ∣ Λ 0 ∣ v 0 / 2 ∣ Σ i ∣ ( v 0 + p + 1 ) / 2 e x p [ − 1 2 t r ( Σ i − 1 Λ 0 ) ] μ i ∣ Σ i ∽ N p ( μ 0 , Σ i k 0 ) = k 0 1 / 2 ( 2 π ) p / 2 ∣ Σ i ∣ 1 / 2 e x p [ − k 0 2 ( μ i − μ 0 ) T Σ i − 1 ( μ i − μ 0 ) ] p ( μ i , Σ i ) = p ( Σ i ) p ( μ i ∣ Σ i ) = I W p ( v 0 , Λ 0 ) N p ( μ 0 , Σ i k 0 ) \begin{aligned} \Sigma_{i} \backsim IW_{p}(v_{0}, \Lambda_{0}) = k_{i} {|\Lambda_{0}|^{v_{0}/2} \over |\Sigma_{i}|^{(v_{0}+p+1)/2}}exp[-{1\over 2}tr(\Sigma_{i}^{-1}\Lambda_{0})] \\ \mu_{i}|\Sigma_{i} \backsim N_{p}(\mu_{0}, {\Sigma_{i} \over k_{0}}) = {k_{0}^{1/2} \over (2\pi)^{p/2}|\Sigma_{i}|^{1/2}}exp[-{k_{0} \over 2}(\mu_{i}-\mu_{0})^{T}\Sigma_{i}^{-1}(\mu_{i}-\mu_{0})] \\ p(\mu_{i}, \Sigma_{i}) =p(\Sigma_{i})p(\mu_{i}|\Sigma_{i}) =IW_{p}(v_{0}, \Lambda_{0}) N_{p}(\mu_{0}, {\Sigma_{i} \over k_{0}}) \end{aligned} Σi∽IWp(v0,Λ0)=ki∣Σi∣(v0+p+1)/2∣Λ0∣v0/2exp[−21tr(Σi−1Λ0)]μi∣Σi∽Np(μ0,k0Σi)=(2π)p/2∣Σi∣1/2k01/2exp[−2k0(μi−μ0)TΣi−1(μi−μ0)]p(μi,Σi)=p(Σi)p(μi∣Σi)=IWp(v0,Λ0)Np(μ0,k0Σi) 参数是 μ 0 , k 0 , v 0 , Λ 0 \mu_{0}, k_{0}, v_{0}, \Lambda_{0} μ0,k0,v0,Λ0 由贝叶斯定理知道,后验正比于似然乘以先验。所以 p ( μ i , Σ i ∣ X i ˉ , V i ) ∝ L ( X i ˉ , V i ∣ μ i , Σ i ) p ( μ i , Σ i ) p(\mu_{i}, \Sigma_{i}| \bar{X_{i}}, V_{i}) \propto L(\bar{X_{i}}, V_{i}|\mu_{i}, \Sigma_{i})p(\mu_{i}, \Sigma_{i}) p(μi,Σi∣Xiˉ,Vi)∝L(Xiˉ,Vi∣μi,Σi)p(μi,Σi) 至此,我们得到了后验分布,后验分布也是一个正态-逆Wishart分布,参数是
μ
n
,
Σ
n
,
v
n
,
Λ
n
\mu_{n}, \Sigma_{n}, v_{n}, \Lambda_{n}
μn,Σn,vn,Λn,省略下标
i
i
i,得到:
p
(
μ
,
Σ
∣
D
,
μ
0
,
k
0
,
v
0
,
Λ
0
)
=
N
I
W
(
μ
,
Σ
∣
μ
n
,
k
n
,
v
n
,
Λ
n
)
(*)
\tag{*} p(\mu, \Sigma|D, \mu_{0}, k_{0}, v_{0}, \Lambda_{0}) = NIW(\mu, \Sigma|\mu_{n}, k_{n}, v_{n}, \Lambda_{n})
p(μ,Σ∣D,μ0,k0,v0,Λ0)=NIW(μ,Σ∣μn,kn,vn,Λn)(*) 通过边缘化(*)式,边缘概率分布为: |
【本文地址】
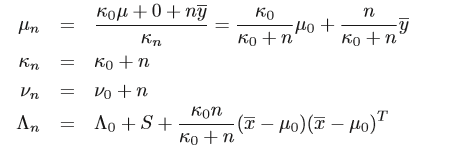 上面,
x
ˉ
=
y
ˉ
\bar{x}=\bar{y}
xˉ=yˉ为样本均值,
s
s
s为样本平方误差。
上面,
x
ˉ
=
y
ˉ
\bar{x}=\bar{y}
xˉ=yˉ为样本均值,
s
s
s为样本平方误差。 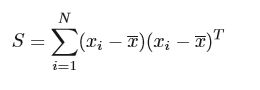
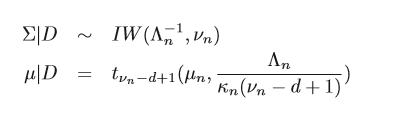 这样就求得了后验分布的解析形式。
这样就求得了后验分布的解析形式。