| 图论算法(七)最小生成树Kruskal算法与(严格)次小生成树 | 您所在的位置:网站首页 › 多个集合交集的最小值是什么 › 图论算法(七)最小生成树Kruskal算法与(严格)次小生成树 |
图论算法(七)最小生成树Kruskal算法与(严格)次小生成树
|
吐槽:严格次小生成树我调了将近10个小时……(虽然有3个小时的电竞时间 Part 1:最小生成树\(Kruskal\)算法 前言介于我们之前已经讨论过最小生成树的定义和\(Prim\)算法了,这次我们直奔主题——\(Kruskal\)算法 \(Kruskal\)算法工作方式还是老样子,我们抛开正确性不谈,只谈算法工作方式和代码实现 \(Kruskal\)的思路非常暴躁:把每个点看成是一个单独的连通块,然后把边按照边权排序,从小到大一条一条加入最小生成树,这样直到有\(n-1\)条边被加入了最小生成树 注意每次加入边的时候,至少有原来不连通的两连通块被联通,这样才能够保证不会形成环 为什么不满足上面的条件就会形成环? 显然易见,如果两个点在加入这条边之前,已经可以相互到达了(成为一个连通块),那么这条边就是多余的,在连接之后会形成重边或者环 每一个连通块都是一个无根树,在树上任意两点之间加一条边,一定会形成一个环,所以为了不形成环,我们不加这条边 让我们举一个生动形象的例子(因为电脑画图实在不方便,这里改成手画了)
我们模拟\(Kruskal\),每个点全都分开,从小到大加入边
然后这样我们就得到了这个图的最小生成树(不唯一),它的大小为\(7\) \(Kruskal\)算法实现方式在算法中,有一个很重要的步骤,就是维护每一条边连通的两个点是不是处于同一个连通块之内,如果处于同一连通块之内,那么这条边是不能被加入最小生成树的 所以我们需要一种数据结构来维护各个连通块的情况,而并查集就很好的满足了我们的要求 PS:不知道什么是并查集?请戳这里 维护一个有\(n\)个集合(每个集合代表一个点)的并查集,初始时每个集合中只有一个元素(点\(i\)) \(1、\)对于每次加边之前,查询两个端点\(a,b\)是否在同一集合里,如果不在同一集合里,执行\(2\),如果在同一集合,那么说明\(a,b\)已经连通了,跳过这条边 \(2、\)把这条边计入最小生成树,然后合并点\(a,b\)所在的集合 \(Code\) #include #include #include #include #include #include #include #include #include #include #include #include #include #include typedef long long int ll; inline int read(){ int fh=1,x=0; char ch=getchar(); while(ch'9'){ if(ch=='-') fh=-1;ch=getchar(); } while('0' |
【本文地址】
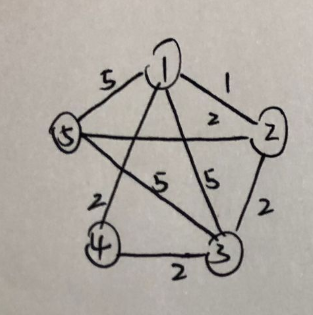 比如像上面这张带权无向图:
比如像上面这张带权无向图: 重复这个操作一直从小到大的加边,直到完成最小生成树
重复这个操作一直从小到大的加边,直到完成最小生成树
