复分析(9)

本篇内容以辐角原理为中心来介绍，而这个定理直接应用于方程在复数域中的某个区域内的根个数，下面就是主要内容：

在介绍辐角原理之前先介绍一个引理

利用上述的引理可以得到我们想要的辐角原理

下面有几个注意的地方

下面我们结合留数的几何意义可以得出

周线 \( C:z=\lambda \left( t \right) \ \left( \alpha \le t\le \beta \right) \ \lambda \left( \alpha \right) =\lambda \left( \beta \right) \) 在变换 \( \omega =f\left( z \right) \) 下的像为 \( \Gamma :\omega =f\left( \lambda \left( t \right) \right) =\mu \left( t \right) \)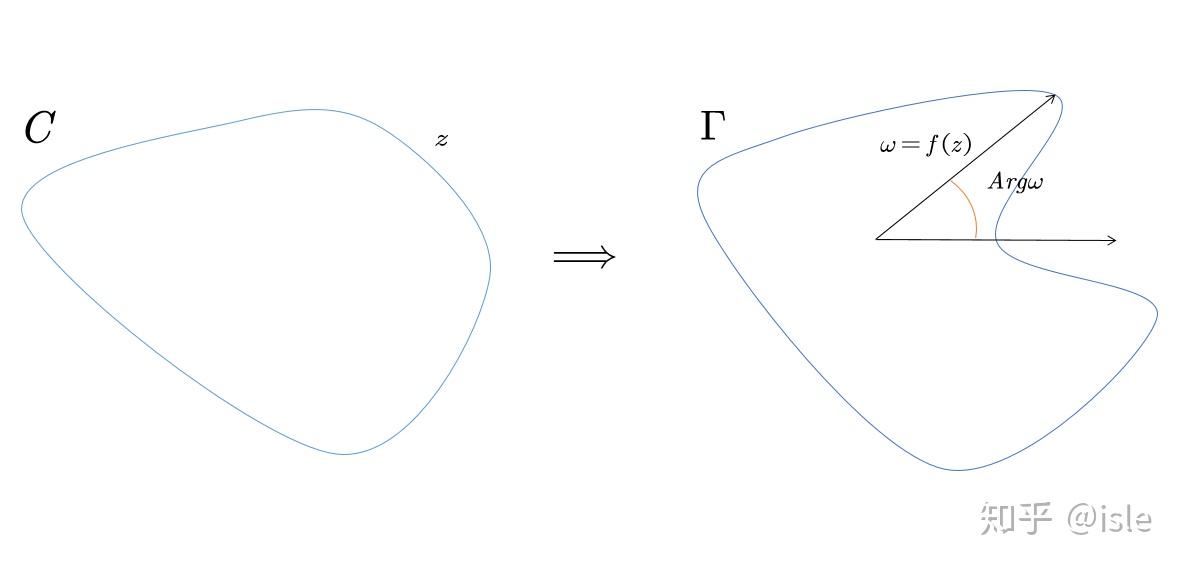

则辐角原理中我们所研究的积分 \( \frac{1}{2\pi}\Delta_Cargf(z)=\frac{1}{2\pi i}\int_C{\frac{f'\left( z \right)}{f\left( z \right)}dz}=\frac{1}{2\pi i}\int_{\Gamma}{\frac{d\omega}{\omega}} \)

对于 \frac{1}{\omega} 有

从而 \( \frac{1}{2\pi i}\int_{\Gamma}{\frac{d\omega}{\omega}} \) 为 \Gamma 围绕原点的正向圈和负向圈数的代数和，所以我们可以得出下面的辐角定理的另一种形式

下面介绍Rouche定理

这个定理说明了和函数零点的个数取决于模较大函数在周线 C 中的零点个数

辐角原理的应用

例9.1

计算积分 \( \frac{1}{2\pi i}\int_{|z|=4}{\frac{z^9}{z^{10}-1}dz} \)