| 有序与无序(Order and disorder) | 您所在的位置:网站首页 › 在无序中发现有序 › 有序与无序(Order and disorder) |
有序与无序(Order and disorder)
|
文章目录
1. 有序的表征1.1 晶格周期性和 X 射线结晶度(Lattice periodicity and X-ray crystallinity)1.2 长程有序(Long-range order)
2. 淬火无序(Quenched disorder)3. 退火无序(Annealed disorder)4. 拓扑序(Topological order)4.1 背景4.2 发现和表征4.3 机制4.4 数学表达式4.5 应用4.6 潜在影响4.7 拓扑熵(Topological entropy)
在物理学中,术语有序(order)和无序(disorder)表示多粒子系统中是否存在某种对称性(symmetry)或相关性(correlation)。 在凝聚态物理学中,系统通常在低温下进行排序。加热后,它们会经历一个或几个相变,变成不太有序的状态。这种有序-无序转换的例子是: 冰的融化:固液转变,失去结晶有序;通过加热到居里温度以上使铁退磁:铁磁-顺磁转变,磁序丢失。有序或无序的自由度可以是平移(晶体有序(crystalline ordering))、旋转(铁电有序(ferroelectric ordering))或自旋态(磁有序(magnetic ordering))。 该有序可以包含在完整的晶体空间群对称中,也可以包含在相关中。根据相关性如何随距离衰减,可以说是长程有序或短程有序。 如果无序状态不处于热力学平衡状态,则称为淬灭无序(quenched disorder)。例如,通过淬火(过冷)液体获得玻璃。进一步推广,其他淬火状态称为自旋玻璃(spin glass),定向玻璃(orientational glass)。在某些情况下,淬火无序的反面是退火无序(annealed disorder)。 1. 有序的表征 1.1 晶格周期性和 X 射线结晶度(Lattice periodicity and X-ray crystallinity)固体中最严格的有序形式是晶格周期性(lattice periodicity):某种特定模式(晶胞中原子的排列)一次又一次地重复,以形成平移不变的空间平铺。这是晶体的定义属性。可能的对称性已被分类为 14 个布拉维格(Bravais lattices)和 230 个空间群(space groups)。 晶格周期性意味着长程有序:如果只知道一个晶胞,那么凭借平移对称性,就可以准确预测任意距离处的所有原子位置。在 20 世纪的大部分时间里,相反的情况也被认为是理所当然的——直到 1982 年准晶体(quasicrystals)的发现表明存在不具有晶格周期性的完美确定性平铺。 除了结构有序之外(structural order),还可以考虑电荷有序(charge ordering)、自旋有序、磁有序(magnetic ordering)和成分有序(compositional ordering)。在中子衍射中可以观察到磁有序。 它是一个热力学熵概念,通常由二级相变显示。一般来说,高热能与无序相关,低热能与有序相关,但也有违反这一点的。在低能量的衍射实验中,有序峰变得明显。 1.2 长程有序(Long-range order)长程有序表征物理系统,其中同一样本的相距较远的不同部分表现出相关行为。 这可以表示为一个相关函数,即自旋-自旋相关函数(spin-spin correlation function): G ( x , x ′ ) = ⟨ s ( x ) , s ( x ′ ) ⟩ G(x,x')=\langle s(x),s(x')\rangle G(x,x′)=⟨s(x),s(x′)⟩ 其中 s s s 是自旋量子数, x x x 是特定系统内的距离函数。 该函数在 x = x ′ x=x' x=x′ 时等于一个单位元,并且随着距离 ∣ x − x ′ ∣ |x-x'| ∣x−x′∣ 而减小。增加。通常,它在远距离处以指数方式衰减到零,并且系统被认为是无序的。但是如果相关函数衰减到一个较大的常数值 ∣ x − x ′ ∣ |x-x'| ∣x−x′∣ 则称该系统具有长程有序。如果它作为距离的幂衰减到零,则称为准远程有序(quasi-long-range)。请注意,什么构成了 ∣ x − x ′ ∣ |x-x'| ∣x−x′∣ 的大值。是在渐近(asymptotics)意义上理解的。 2. 淬火无序(Quenched disorder)在统计物理学中,当定义系统行为的某些参数是不随时间演变的随机变量时,即它们被淬火或冻结时,系统被称为呈现淬火无序(quenched disorder)。自旋就是一个典型的例子。它与退火无序(annealed disorder)相反,后者允许随机变量自行演化。 在数学领域中,淬火无序比退火无序更难分析,因为热平均和噪声平均起着非常不同的作用。事实上,这个问题是如此之难,以至于几乎没有已知的解决方法,其中大多数都依赖于近似值。最常用的方法是: 一种基于称为复本技巧(replica trick)的数学分析延拓的技术;空腔法(cavity method);尽管这些给出的结果与大量问题的实验结果一致,但它们通常未被证明是一个严格的数学过程。然而,最近通过严格的方法表明,至少在原型自旋玻璃模型( archetypal spin-glass model,所谓的 Sherrington-Kirkpatrick 模型)中,基于复本的解决方案确实是精确的。 该领域第二常用的技术是生成函数分析(generating functional analysis)。这种方法基于路径积分,原则上是完全精确的,尽管通常比复本过程更难应用。  图 从无序(左)到有序(右)状态的转变
3. 退火无序(Annealed disorder)
图 从无序(左)到有序(右)状态的转变
3. 退火无序(Annealed disorder)
当系统定义中的某些参数是随机变量,但其演化与定义系统的自由度的演化相关时,系统被称为呈现退火无序(annealed disorder)。它的定义与淬火无序相反,其中随机变量可能不会改变它们的值。 具有退火无序的系统通常被认为更容易在数学上处理,因为无序的平均值和热平均值可以在相同的基础上处理。 4. 拓扑序(Topological order)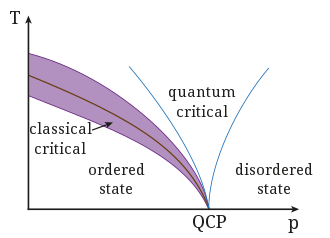 图 从无序(左)到有序(右)状态的转变
图 从无序(左)到有序(右)状态的转变
在物理学中,拓扑序(topological order)是物质相(也称为量子物质)在零温度下的一种有序。宏观上,拓扑序由稳健的基态退化(ground state degeneracy)和退化基态(degenerate ground states)的量化非阿贝尔几何相位(geometric phase)定义和描述。在微观上,拓扑序对应于长程量子纠缠的模式。具有不同拓扑序(或不同的长程纠缠模式)的状态在没有相变的情况下不能相互改变。 各种拓扑有序状态具有有趣的性质,例如(1)拓扑简并(topological degeneracy)和分数统计(fractional statistics)或非阿贝尔统计(non-abelian statistics)可用于实现拓扑量子计算机;(2)可能具有重要器件应用的完美导电边缘状态(conducting edge states);(3)涌现规范场和费米统计表明基本粒子的量子信息起源;(4)拓扑纠缠熵(topological entanglement entropy)揭示了拓扑序的纠缠起源等。拓扑序在几个物理系统的研究中很重要例如自旋液体和量子霍尔效应,以及容错量子计算的潜在应用。 拓扑绝缘体和拓扑超导体(超过一维)没有上述定义的拓扑序,它们的纠缠只是短程的。 4.1 背景尽管所有物质都是由原子组成的,但物质可以具有不同的性质,并以不同的形式出现,如固体、液体、超流体等。这些不同形式的物质通常被称为物质的状态或相。根据凝聚态物理和涌现原理,材料的不同性质源于原子在材料中的不同组织方式。原子(或其他粒子)的这些不同组织在形式上被称为材料中的序。 原子可以以多种方式组织,从而导致许多不同的序和许多不同类型的材料。朗道对称破缺理论提供了对这些不同序的一般理解。它指出不同的序实际上对应于组成原子组织中的不同对称性。当材料从一个序变为另一个序时(即,当材料经历相变时),所发生的是原子组织的对称性发生变化。 例如,原子在液体中具有随机分布,因此当我们将原子置换任意距离时,液体保持不变。我们说液体具有连续平移对称性。在相变之后,液体可以变成晶体。在晶体中,原子组织成规则的阵列(晶格)。只有当我们将晶格位移特定距离(整数乘以晶格常数)时,晶格才会保持不变,因此晶体只有离散的平移对称性。液体和晶体之间的相变是将液体的连续平移对称性降低为晶体的离散对称性的转变。这种对称性的变化称为对称性破缺。因此,液体和晶体之间差异的本质是原子的组织在两相中具有不同的对称性。 朗道对称破缺理论一直是一个非常成功的理论。长期以来,物理学家认为朗道理论描述了材料中所有可能的序,以及所有可能的(连续)相变。 4.2 发现和表征然而,自 1980 年代后期以来,Landau 对称破缺理论可能无法描述所有可能的序逐渐变得明显。为了解释高温超导性,引入了手征自旋态(chiral spin state)。起初,物理学家还想用朗道对称破缺理论来描述手征自旋态。他们将手性自旋状态确定为打破时间反转和奇偶对称性的状态,而不是自旋旋转对称性。根据朗道的对称破缺描述,这应该是故事的结局。然而,人们很快意识到有许多不同的手征自旋态具有完全相同的对称性,因此仅靠对称性不足以表征不同的手征自旋态。这意味着手性自旋态包含一种超出通常对称性描述的新秩序。提议的新秩序被命名为“拓扑秩序”。“拓扑序”这个名称的灵感来自手征自旋态的低能量有效理论(low energy effective theory),它是一种拓扑量子场论 (topological quantum field theory,TQFT)。新的量子数,例如基态简并(可以定义在封闭空间或具有间隙边界的开放空间上,包括阿贝尔拓扑序和非阿贝尔拓扑序)和简并基态的非阿贝尔几何相位,被引入来表征和定义手性自旋态的不同拓扑阶。最近,表明拓扑顺序也可以用拓扑熵来表征。 但是实验很快表明手性自旋态不能描述高温超导体,拓扑序理论变成了一个没有实验实现的理论。然而,手性自旋态和量子霍尔态之间的相似性使得人们可以使用拓扑序理论来描述不同的量子霍尔态。就像手性自旋态一样,不同的量子霍尔态都具有相同的对称性,并且在朗道对称破缺描述之外。发现不同量子霍尔态的不同序确实可以用拓扑序来描述,所以拓扑确实有实验实现。 分数量子霍尔(fractional quantum Hall,FQH)态是在 1989 年引入拓扑序概念之前于 1982 年发现的。但 FQH 态并不是第一个通过实验发现的拓扑序态。 1911 年发现的超导体是第一个通过实验发现的拓扑序状态。它具有 Z 2 \mathsf{Z}_{2} Z2 拓扑序。 虽然拓扑序态通常出现在强相互作用的玻色子/费米子系统中,但一种简单的拓扑序也可以出现在自由费米子系统中。这种拓扑序对应于积分量子霍尔态,如果我们考虑晶格上的整数量子霍尔态,则可以用填充能带的陈数(Chern number)来表征。理论计算表明,这种陈数可以通过实验测量自由费米子系统。众所周知,这样的陈数可以(可能间接地)通过边缘状态来测量。 拓扑序最重要的特征是潜在的分数激发(例如 anyons)及其 fusion statistics 和braiding statistics(可以超越玻色子或费米子的量子统计)。目前的研究工作表明,3+1 维时空中的拓扑序存在环和弦状激发,它们的多环/弦 braiding statistics 是识别 3+1 维拓扑序的关键特征。3+1 维拓扑序的 multi-loop/string-braiding statistics 可以通过特定拓扑量子场论在 4 个时空维度的链接不变量来捕获。 4.3 机制一大类 2+1D 拓扑序是通过一种称为 string-net condensation 的机制实现的。这类拓扑序可以有一个间隙边缘,并由unitary fusion category (or monoidal category) theory 分类。人们发现 string-net condensation 可以产生无限多种不同类型的拓扑序,这可能表明还有许多不同的新型材料有待发现。 Condensed strings 的集体运动产生高于 string-net condensation 的激发。这些激发结果是规范玻色子。弦的末端是对应于另一种激励的缺陷。这些激发是规范电荷,可以携带费米或分数统计。 其他扩展对象如“membranes”、“brane-nets”和分形(fractals)的凝聚也会导致拓扑序相和“量子玻璃性(quantum galssiness)”。 4.4 数学表达式我们知道群论是对称破缺序的数学基础。拓扑序的数学基础是什么?发现 2+1D 拓扑序的一个子类——阿贝尔拓扑序——可以通过 K K K 矩阵方法进行分类。string-net condensation 表明张量范畴(如 fusion category 或 monoidal category)是 2+1D 拓扑序的数学基础的一部分。最近的研究表明(直到没有分级激发的可逆拓扑阶): 2+1D 玻色子拓扑阶按 unitary modular tensor categories 分类。具有对称性 G 的 2+1D 玻色子拓扑序按 G-crossed tensor categories 分类。具有对称性 G 的 2+1D 玻色子/费米子拓扑序按 unitary braided fusion categories 而非 symmetric fusion category 进行分类,该类别具有 modular extensions。玻色子系统的 symmetric fusion category Rep(G) 和费米子系统的 sRep(G)。更高维度的拓扑序可能与 n 范畴理论(n-Category theory)有关。量子算子代数是研究拓扑序的非常重要的数学工具。 一些人还认为,拓扑序在数学上是通过扩展的量子对称性(extended quantum symmetry)来描述的。 4.5 应用朗道对称破缺理论所描述的材料对技术产生了重大影响。例如,破坏自旋旋转对称性的铁磁材料可以用作数字信息存储的介质。由铁磁材料制成的硬盘驱动器可以存储千兆字节的信息。打破分子旋转对称性的液晶在显示技术中得到广泛应用。打破平移对称性的晶体会导致明确定义的电子能带,从而使我们能够制造半导体器件,例如晶体管。不同类型的拓扑序甚至比不同类型的对称破缺序更丰富。这表明它们具有令人兴奋的新颖应用的潜力。 一个理论上的应用是在一种称为拓扑量子计算的技术中使用拓扑序状态作为量子计算的媒介。拓扑序状态是具有复杂非局部量子纠缠的状态。非定域性意味着处于拓扑序状态的量子纠缠分布在许多不同的粒子之间。因此,量子纠缠的模式不能被局部扰动破坏。这显着降低了退相干的影响。这表明,如果我们在拓扑序状态下使用不同的量子纠缠来编码量子信息,则信息可能会持续更长时间。拓扑量子纠缠编码的量子信息也可以通过相互拖动拓扑缺陷来操纵。这个过程可能会提供一种用于执行量子计算的物理设备。因此,拓扑序状态可以为量子记忆和量子计算提供自然介质。量子存储器和量子计算的这种实现可能具有容错性。 拓扑序状态通常具有一个特殊的性质,即它们包含非平凡的边界状态。在许多情况下,这些边界状态成为完美的导电通道,可以在不产生热量的情况下导电。这可能是拓扑序在电子设备中的另一个潜在应用。 与拓扑序类似,拓扑绝缘体也具有无间隙边界状态(gapless boundary states)。拓扑绝缘体的边界状态在拓扑绝缘体的检测和应用中起着关键作用。这种观察自然会引出一个问题:拓扑绝缘体是拓扑序状态的例子吗?事实上,拓扑绝缘体与本文定义的拓扑有序状态不同。拓扑绝缘体只有短程纠缠,没有拓扑序,而本文定义的拓扑序是长程纠缠的一种模式。拓扑序对任何扰动都是稳健的。它具有涌现规范理论、涌现分数电荷和分数统计。相比之下,拓扑绝缘体仅对尊重时间反转和 U ( 1 ) U(1) U(1) 对称性的扰动具有鲁棒性。它们的准粒子激发没有分数电荷和分数统计。严格来说,拓扑绝缘体是 symmetry-protected topological (SPT) order 的一个例子,其中 SPT 序的第一个例子是 spin-1 chain 的 Haldane phase。但 spin-2 chain 的 Haldane phase 没有 SPT 序。 4.6 潜在影响朗道对称破缺理论是凝聚态物理的基石。它用于定义凝聚态研究的领域。拓扑序的存在似乎表明自然界比朗道对称破缺理论迄今为止所表明的要丰富得多。所以拓扑序开辟了凝聚态物理的新方向——高度纠缠量子物质的新方向。我们意识到物质的量子相(即物质的零温度相)可以分为两类:长程纠缠态和短程纠缠态。拓扑序是描述长程纠缠状态的概念:拓扑序 = 长程纠缠模式。短程纠缠态在它们都属于一个相的意义上是微不足道的。然而,在存在对称性的情况下,即使是短程纠缠态也是非平凡的,并且可以属于不同的相。据说这些相包含 SPT 序。SPT 序将拓扑绝缘体的概念推广到相互作用系统。 一些人认为,局部玻色子(自旋)模型中的拓扑顺序(或更准确地说,string-net condensation)有可能为我们宇宙中的光子、电子和其他基本粒子提供统一的起源。 4.7 拓扑熵(Topological entropy)拓扑纠缠熵或拓扑熵,通常用 γ \gamma γ 表示,是一个表征具有拓扑序的多体状态的数(many-body states)。 非零拓扑纠缠熵(non-zero topological entanglement entropy)反映了多体量子态中长程量子纠缠的存在。因此,拓扑纠缠熵将拓扑序与长程量子纠缠的模式联系起来。 给定一个拓扑有序状态,拓扑熵可以从测量空间块与系统其余部分之间的量子纠缠的冯诺依曼熵的渐近行为中提取。在无限二维拓扑序状态内,边界长度为 L L L 的简单连接区域的纠缠熵对于大 L L L 具有以下形式: S L ⟶ α L − γ + O ( L − ν ) , ν > 0 {\displaystyle S_{L}\;\longrightarrow \;\alpha L-\gamma +{\mathcal {O}}(L^{-\nu })\;,\qquad \nu >0\,\!} SL⟶αL−γ+O(L−ν),ν>0 其中 − γ -\gamma −γ 是拓扑纠缠熵。 拓扑纠缠熵等于状态的准粒子激发的总量子维度的对数。 例如,最简单的分数量子霍尔态,即填充分数 1 / m 1/m 1/m 处的 Laughlin 态,具有 γ = 1 / 2 log ( m ) \gamma=1/2\log(m) γ=1/2log(m)。 Z 2 \mathsf{Z}_{2} Z2 分数化状态(fractionalized states),例如 Z 2 \mathsf{Z}_{2} Z2 自旋液体的拓扑有序状态、非二分晶格上(non-bipartite lattices)的量子二聚体模型(quantum dimer models),以及 Kitaev’s toric code state,均以 γ = log ( 2 ) \gamma = \log(2) γ=log(2) 为特征。 参考文献wiki: Order and disorder wiki: Short range order wiki: Topological entropy in physics wiki: Topological order |
【本文地址】