四元数与欧拉角（RPY角）的相互转换

　　描述坐标系{B}相对于参考坐标系{A}的姿态有两种方式。第一种是绕固定（参考）坐标轴旋转：假设开始两个坐标系重合，先将{B}绕{A}的X轴旋转$\gamma$，然后绕{A}的Y轴旋转$\beta$，最后绕{A}的Z轴旋转$\alpha$，就能旋转到当前姿态。可以称其为X-Y-Z fixed angles或RPY角(Roll, Pitch, Yaw)。

　　Roll:横滚

　　Pitch: 俯仰

Yaw: 偏航（航向）

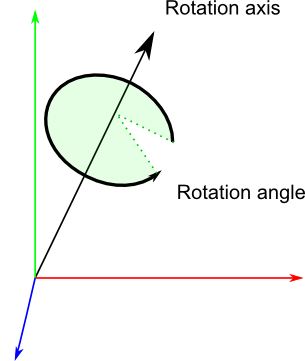
　　由于是绕固定坐标系旋转，则旋转矩阵为（$c\alpha$ is shorthand for $\cos\alpha$, $s\alpha$ is shorthand for $\sin\alpha$,and so on.）

$$R_{XYZ}(\gamma,\beta,\alpha)=R_Z(\alpha)R_Y(\beta)R_X(\gamma)=\begin{bmatrix}c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\ s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\ -s\beta& c\beta s\gamma & c\beta c\gamma\end{bmatrix}$$

　　另一种姿态描述方式是绕自身坐标轴旋转：假设开始两个坐标系重合，先将{B}绕自身的Z轴旋转$\alpha$，然后绕Y轴旋转$\beta$，最后绕X轴旋转$\gamma$，就能旋转到当前姿态。称其为Z-Y-X欧拉角，由于是绕自身坐标轴进行旋转，则旋转矩阵为：

$$R_{Z'Y'X'}(\alpha,\beta,\gamma)=R_Z(\alpha)R_Y(\beta)R_X(\gamma)=\begin{bmatrix}c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\ s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\ -s\beta& c\beta s\gamma & c\beta c\gamma\end{bmatrix}$$

　　可以发现这两种描述方式得到的旋转矩阵是一样的，即绕固定坐标轴X-Y-Z旋转$(\gamma,\beta,\alpha)$和绕自身坐标轴Z-Y-X旋转$(\alpha,\beta,\gamma)$的最终结果一样，只是描述的方法有差别而已。In gerenal: three rotations taken about fixed axes yield the same final orientation as the same three rotations taken in opposite order about the axes of the moving frame.

　　绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度。假设等效旋转轴方向向量为$\vec{K}=[k_x,k_y,k_z]^T$，等效旋转角为$\theta$，则四元数$q=(x,y,z,w)$，其中：

$$\begin{align*} x &= k_x \cdot sin \frac{\theta}{2}\\y &= k_y \cdot sin \frac{\theta}{2}\\z &= k_z \cdot sin \frac{\theta}{2}\\w &= cos \frac{\theta}{2}\end{align*}$$

　　且有$x^2+y^2+z^2+w^2=1$

　　即四元数存储了旋转轴和旋转角的信息，它能方便的描述刚体绕任意轴的旋转。

　　四元数转换为旋转矩阵：

$$R=\begin{bmatrix}1-2y^2-2z^2 & 2(xy-zw) & 2(xz+yw)\\ 2(xy+zw) & 1-2x^2-2z^2 & 2(yz-xw)\\ 2(xz-yw)& 2(yz+xw) & 1-2x^2-2y^2\end{bmatrix}$$

 　　已知旋转矩阵为：

　　则对应的四元数为：

　　定义两个四元数：

四元数加法：

四元数乘法：

　　四元数的乘法的意义类似于矩阵的乘法，可以表示旋转的合成。当有多次旋转操作时，使用四元数可以获得更高的计算效率。