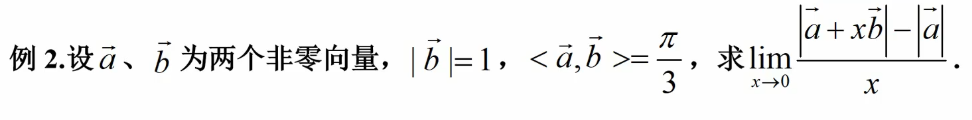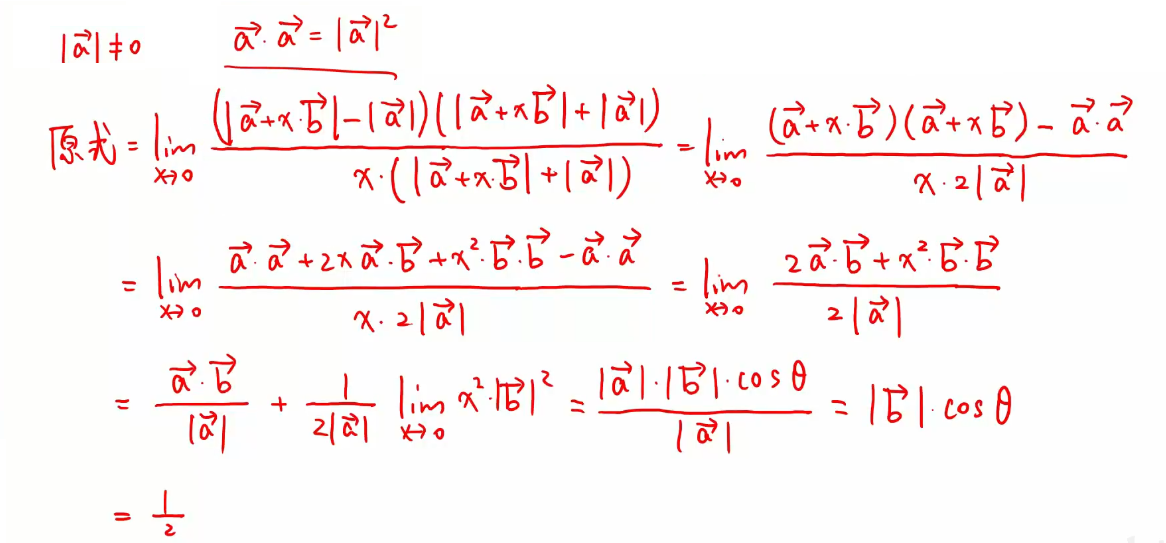| 空间解析几何 | 您所在的位置:网站首页 › 向量几何表示法的定义 › 空间解析几何 |
空间解析几何
|
一、向量及其运算
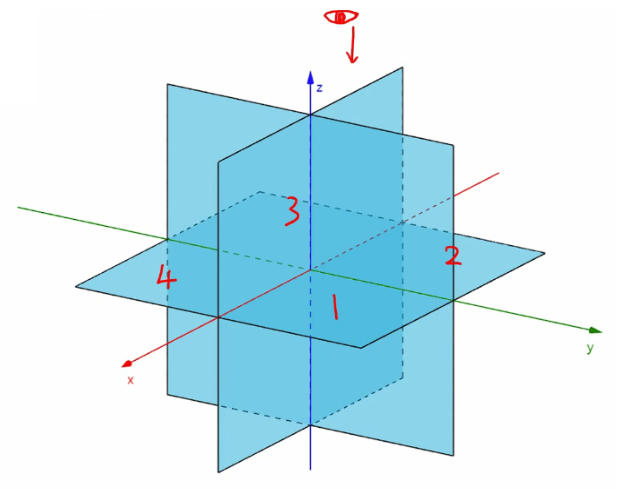
1、空间直角坐标系
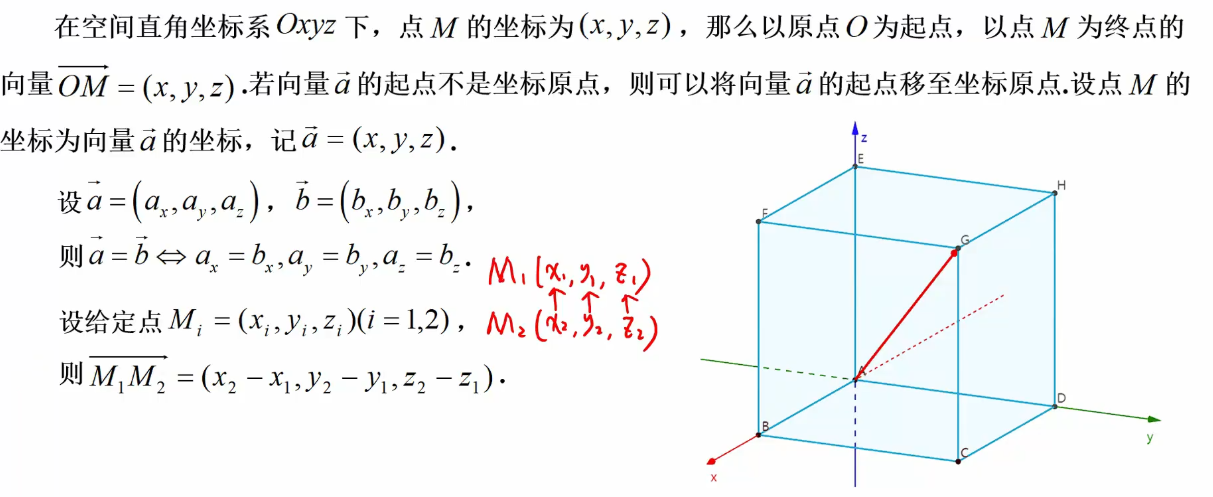
注: 通过公式我们可以发现,两个向量的数量积就是一个数量。 数量积又称为点积或者内积。 ex: 在直角坐标系 {O; i, j, k} 中,设 α = (a1, a2, a3), β = (b1, b2, b3), α • β = (a1i + a2j + a3k) • (b1i + b2j + b3k) = a1b1 + a2b2 + a3b3 即两向量的数量积之和等于它们对应坐标的乘积之和。
注: 向量积是一个向量, 向量积又称为叉积和外积。 ex: 在直角坐标系 {O; i, j, k} 中,设 α = (a1, a2, a3), β = (b1, b2, b3), α χ β = (a1i + a2j + a3k) χ (b1i + b2j + b3k) = (a2b3 - a3b2) i - (a1b3 - a3b1) j + (a1b2 - a2b1) k 注:
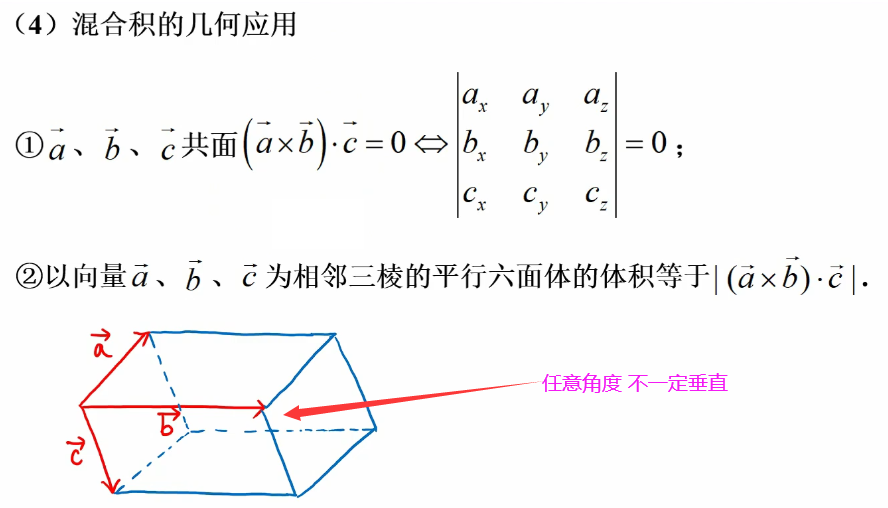
注: 向量α 与 β 的向量积,再与向量 γ 作数量积,其结果为一个数量 (空间向量基本定理)任意给定空间中三个不共面向量 α, β, γ,则空间中任一 向量 ν 可以用 α, β, γ 唯一线性表示,即存在唯一一组实数 x, y, z 使 ν = xα + yβ + zγ
三、距离公式
|
【本文地址】
公司简介
联系我们