| 算术基本定理“质数分解唯一性的证明”:古典方法与现代方法 | 您所在的位置:网站首页 › 合数的另外一个名称 › 算术基本定理“质数分解唯一性的证明”:古典方法与现代方法 |
算术基本定理“质数分解唯一性的证明”:古典方法与现代方法
|
算术基本定理的最早证明是由欧几里得给出的。 每一个比1大的自然数N只能有一种方式分解成质数的乘积。 推论:若一个质数p是乘积ab的因子,则p不是a的因子就是b的因子。 大于1的自然数必可写成质数之积用反证法:假设存在大于1的自然数不能写成质数的乘积,把最小的那个称为n。 自然数可以根据其可除性(是否能表示成两个不是自身的自然数的乘积)分成3类:质数、合数和1。首先,按照定义,n 大于1。其次,n 不是质数,因为质\数p可以写成质数乘积:p=p,这与假设不相符合。因此n只能是合数,但每个合数都可以分解成两个严格小于自身而大于1的自然数的积。设
唯一性
欧几里得《几何原本》和维基百科上的方法都是先证明推论,再证明定理的方法。维基百科的方法可参考:http://zh.wikipedia.org/wiki/%E7%AE%97%E8%A1%93%E5%9F%BA%E6%9C%AC%E5%AE%9A%E7%90%86 欧几里得《几何原本》的介绍可参考:http://dulang.blog.sohu.com/717224.html 欧几里得《几何原本》的证明方法
先证明推论:对应于《几何原本》第7卷第30命题,设(7-30) 命题描述:以现在的数学语言,若质数p|ab,则不p|a就p|b
设c=ab;p为质数,若p量尽a,得证;若p量不尽a(即p不是a的因子),证明p量尽b即得证。 根据(7-29),因为p为质数,且p量不尽a,所以p、a互质。 用反证法证明如下:设p、a不互质,将有公因子m,因为m是a的因子,p不是a的因子,所以m不等于p,而m是p的因子,这是不可能的。 根据(7-定义15),c/p=t,得到c=pt,又c=ab,根据(7-19)得到p/a=b/t 根据(7-21),因为p、a互质,p、a是具有相同比的数对中最小的一对。 再根据(7-20),大小两数a、p分别量尽具有同比的大小两数t、b,所得的次数相同,即前项量尽前项、后项量尽后项,所以p量尽b,即得证。 最后一条定理(7-20)证明的难度较大,特证明如下: 命题:设a、b是与a/b有相同比的数对中最小的一对数,如果a/b=c/d,则a=(1/n)*c;b=(1/n)*d。 证明:因为a |
【本文地址】
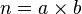 ,其中a 和b 都是介于1和n 之间的自然数,因此,按照n 的定义,a 和b 都都可以写成质数的乘积。从而
,其中a 和b 都是介于1和n 之间的自然数,因此,按照n 的定义,a 和b 都都可以写成质数的乘积。从而