|
向量叉积
 仅在三维空间,两个向量的叉积才有定义,记作 u ^ v 定义为: u ^ v = ||u|| ||v|| sin(θ) n 其中,θ表示u 和 v 的夹角, ||u|| 和 ||v|| 分别是向量 u和v 的模,n 则是u、v 所构成平面的法向(垂直于u、v平面的单位向量),方向由右手定则决定。 仅在三维空间,两个向量的叉积才有定义,记作 u ^ v 定义为: u ^ v = ||u|| ||v|| sin(θ) n 其中,θ表示u 和 v 的夹角, ||u|| 和 ||v|| 分别是向量 u和v 的模,n 则是u、v 所构成平面的法向(垂直于u、v平面的单位向量),方向由右手定则决定。
矩阵表示
叉积可以表示成如下行列式:  其中, u = (u1, u2, u3),v = (v1, v2, v3),i、j、k为基向量,为三维坐标系的x, y, z方向的单位向量。 这个行列式可以使用拉普拉斯在展开和萨吕法则计算。 使用拉普拉斯展开可以沿第一展开为: 其中, u = (u1, u2, u3),v = (v1, v2, v3),i、j、k为基向量,为三维坐标系的x, y, z方向的单位向量。 这个行列式可以使用拉普拉斯在展开和萨吕法则计算。 使用拉普拉斯展开可以沿第一展开为: 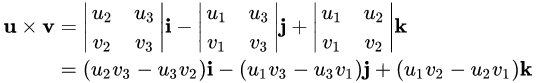 使用萨吕法则可以展开为: 使用萨吕法则可以展开为: 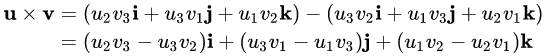
几何意义
根据定义可以得出,向量叉积的几何意义是以u和v为零边的平行四边形的有向面积。
应用
在计算机图形学中,向量叉乘的应用广泛。比如,判断线段的相对位置,线段相交,点在多边形内,求凸包等。
判断两条线段的相对位置
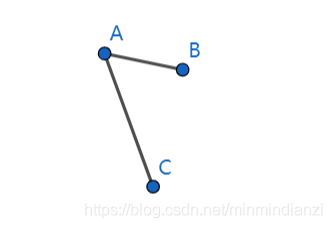 在二维平面上有两条线段,分别是AB和AC,如何通过向量叉积来确定他们的相对位置关系 点A、B、C的坐标为 在二维平面上有两条线段,分别是AB和AC,如何通过向量叉积来确定他们的相对位置关系 点A、B、C的坐标为 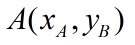   首先构造两个向量AB和AC, 首先构造两个向量AB和AC, 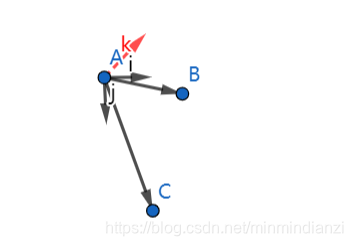 由于二维空间不存在叉积的定义,所以引入z轴,将向量AB、AC扩展到三维空间,可以将二位向量可看作z轴恒为0的三维向量, 那么,两个向量叉积的则可表示为: 由于二维空间不存在叉积的定义,所以引入z轴,将向量AB、AC扩展到三维空间,可以将二位向量可看作z轴恒为0的三维向量, 那么,两个向量叉积的则可表示为:  res > 0, AC在AB的逆时针方向 res = 0, AB和AC共线 res < 0, AC在AB的顺时针方向 res > 0, AC在AB的逆时针方向 res = 0, AB和AC共线 res < 0, AC在AB的顺时针方向
|  仅在三维空间,两个向量的叉积才有定义,记作 u ^ v 定义为: u ^ v = ||u|| ||v|| sin(θ) n 其中,θ表示u 和 v 的夹角, ||u|| 和 ||v|| 分别是向量 u和v 的模,n 则是u、v 所构成平面的法向(垂直于u、v平面的单位向量),方向由右手定则决定。
仅在三维空间,两个向量的叉积才有定义,记作 u ^ v 定义为: u ^ v = ||u|| ||v|| sin(θ) n 其中,θ表示u 和 v 的夹角, ||u|| 和 ||v|| 分别是向量 u和v 的模,n 则是u、v 所构成平面的法向(垂直于u、v平面的单位向量),方向由右手定则决定。 其中, u = (u1, u2, u3),v = (v1, v2, v3),i、j、k为基向量,为三维坐标系的x, y, z方向的单位向量。 这个行列式可以使用拉普拉斯在展开和萨吕法则计算。 使用拉普拉斯展开可以沿第一展开为:
其中, u = (u1, u2, u3),v = (v1, v2, v3),i、j、k为基向量,为三维坐标系的x, y, z方向的单位向量。 这个行列式可以使用拉普拉斯在展开和萨吕法则计算。 使用拉普拉斯展开可以沿第一展开为: 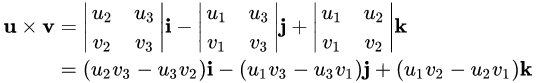 使用萨吕法则可以展开为:
使用萨吕法则可以展开为: 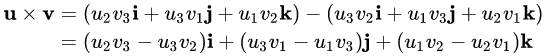
 在二维平面上有两条线段,分别是AB和AC,如何通过向量叉积来确定他们的相对位置关系 点A、B、C的坐标为
在二维平面上有两条线段,分别是AB和AC,如何通过向量叉积来确定他们的相对位置关系 点A、B、C的坐标为 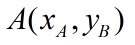

 首先构造两个向量AB和AC,
首先构造两个向量AB和AC,  由于二维空间不存在叉积的定义,所以引入z轴,将向量AB、AC扩展到三维空间,可以将二位向量可看作z轴恒为0的三维向量, 那么,两个向量叉积的则可表示为:
由于二维空间不存在叉积的定义,所以引入z轴,将向量AB、AC扩展到三维空间,可以将二位向量可看作z轴恒为0的三维向量, 那么,两个向量叉积的则可表示为:  res > 0, AC在AB的逆时针方向 res = 0, AB和AC共线 res < 0, AC在AB的顺时针方向
res > 0, AC在AB的逆时针方向 res = 0, AB和AC共线 res < 0, AC在AB的顺时针方向