最优控制理论 二+、哈密尔顿函数法的补充

前面我在第二章最优控制理论 二、哈密尔顿函数法给出了Hamilton函数法一些重要推导过程和一些常用公式。最近翻看，觉得写得太多了，于是把一部分不重要的贴到下面，另成一篇。

第3部分我们只考虑了终端等式约束，但是实际的动力学和控制问题里常有其他类型的等式约束，如

下面可以证明，以上这些等式约束都可以用Hamilton函数法解决。

对 ∫ 0 t f N ( x ( t ) , u ( t ) , t ) d t = β ∈ R q (积分方程约束) \int_0^{t_f}N(x(t),u(t),t)\text d t=\beta\in\Reals^q\tag{积分方程约束} ∫0tf​​N(x(t),u(t),t)dt=β∈Rq(积分方程约束)引入扩充的状态变量 y ( t ) ∈ R q y(t)\in\Reals^q y(t)∈Rq且它满足 y ˙ = N ( x , u , t ) y ( 0 ) = 0 , y ( t f ) = ∫ 0 t f N ( x ( t ) , u ( t ) , t ) d t β (2) \dot y=N(x,u,t)\\ y(0)=0,y(t_f)=\int_0^{t_f}N(x(t),u(t),t)\text d t\beta\tag{2} y˙​=N(x,u,t)y(0)=0,y(tf​)=∫0tf​​N(x(t),u(t),t)dtβ(2)

则把上面这个积分方程约束化为终端状态约束，两个方程等价。仍可套用终端状态约束的框架，需要注意由于状态扩充为 n + q n+q n+q维；并多了 q q q个Lagrange乘乘数，加上原来的 m m m个，共有 m + q m+q m+q个终端约束和 m + q m+q m+q个未知的Lagrange乘数。

设状态变量和等式约束具有以下形式： N ( x ( t ) , u ( t ) , t ) = 0 , t 0 < t < t f (状态+控制等式约束) N(x(t),u(t),t)=0,t_0\lt t\lt t_f\tag{状态+控制等式约束} N(x(t),u(t),t)=0,t0​1,2,…,N}。

此种情况下，在每一个角点处条件是： λ ( t i − ) = λ ( t i + ) + μ T ∂ ψ ( i ) ∂ x (5) \lambda(t_i-)=\lambda(t_i+)+\mathbf\mu^{\mathrm T}\frac{\partial \psi^{(i)}}{\partial\mathbf x}\tag {5} λ(ti​−)=λ(ti​+)+μT∂x∂ψ(i)​(5)

以及内点时间 t i t_i ti​服从 H ( t i + ) = H ( t i − ) + μ T ∂ ψ ( i ) ∂ t (6) H(t_i+)=H(t_i-)+\mathbf\mu^{\mathrm T}\frac{\partial\psi^{(i)}}{\partial t}\tag 6 H(ti​+)=H(ti​−)+μT∂t∂ψ(i)​(6)其中 μ ∈ R q i \mu\in\Reals^{q_i} μ∈Rqi​，对应为该内点约束的Lagrange乘子。以上这个内点约束 ( 5 , 6 ) (5 ,6) (5,6)对于分段连续的状态方程也成立 KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at position 20: …in{aligned}\dot\̲m̲a̲t̲h̲b̲f̲ ̲x&=\left\{\begi…

简单来说就是，Hamiltonian和协态变量 λ ( t ) \lambda(t) λ(t)在每一个内点约束附近发生间断。

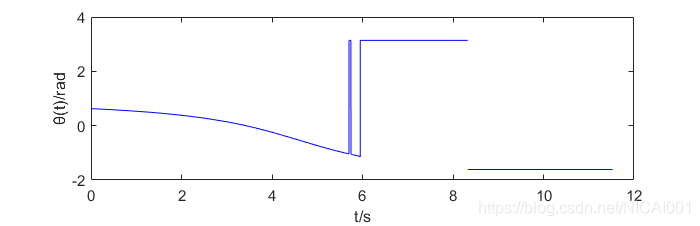
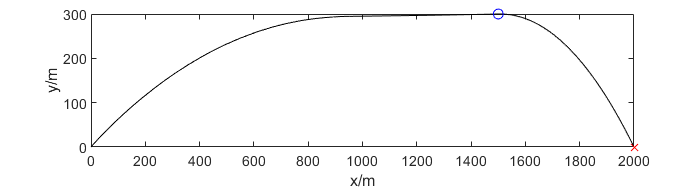
若状态变量 x ( t ) x(t) x(t)是分段函数，在每一段连续可导，而每一段不连续 x ( t i − ) ≠ x ( t i + ) \mathbf x(t_i-)\neq\mathbf x(t_i+) x(ti​−)=x(ti​+)。典型案例如多脉冲轨道转移。如果这样的系统在某些点有内点条件（Interior-Point constraints），问题描述如[2]中3.7节的截图： 此种情况下，如上一章节所定义的标量函数， H ( i ) ≜ L ( i ) + λ T f ( i ) Φ ≜ φ + ∑ j = 0 N [ μ ( i ) ] T ψ ( i ) H^{(i)}\triangleq L^{(i)}+\lambda^{\mathrm T}f^{(i)}\\ \Phi\triangleq \varphi+\sum_{j=0}^{N}[\mu^{(i)}]^{\mathrm T}\psi^{(i)} H(i)≜L(i)+λTf(i)Φ≜φ+j=0∑N​[μ(i)]Tψ(i)

间断点处的状态变量不连续，但遵循约束条件；协态变量有： λ T ( t i − ) = ∂ Φ ∂ x ( t i − ) ;   i = 1 , … , N λ T ( t i + ) = − ∂ Φ ∂ x ( t i + ) ;   i = 0 , … , N − 1 , (7) \begin{aligned} &\lambda^{T}\left(t_{i}-\right)=\frac{\partial \Phi}{\partial x\left(t_{i}-\right)} ; \ i=1, \ldots, N \\ &\lambda^{T}\left(t_{i}+\right)=-\frac{\partial \Phi}{\partial x\left(t_{i}+\right)} ; \ i=0, \ldots, N-1, \end{aligned}\tag 7 ​λT(ti​−)=∂x(ti​−)∂Φ​; i=1,…,NλT(ti​+)=−∂x(ti​+)∂Φ​; i=0,…,N−1,​(7)

如果内点的到达时间未 t i t_i ti​指定，还有哈密尔顿函数服从以下 N N N个式子： H ( i + 1 ) ( t i + ) = ∂ Φ ∂ t i + H ( i ) ( t i − ) , i = 0 , … , N H^{(i+1)}\left(t_{i+}\right)= \frac{\partial \Phi}{\partial t_{i}}+H^{(i)}\left(t_{i-}\right), \quad i=0, \ldots, N H(i+1)(ti+​)=∂ti​∂Φ​+H(i)(ti−​),i=0,…,N

控制变量由 x ( t ) x(t) x(t)和 λ ( t ) \lambda(t) λ(t)推导得到。这个问题的实例以及其求解方法可见沈红新博士论文[4]。

最短时间拦截且飞行中途经过一个点的问题，如下 min ⁡ θ ( t ) J = t f s.t. { x ˙ = u ,   y ˙ = v u ˙ = a cos ⁡ θ ,   v ˙ = a sin ⁡ θ \min_{\theta(t)}J=t_f\\ \text{s.t.}\left\{\begin{matrix}\dot x=u,\ \dot y=v\\ \dot u=a\cos\theta,\ \dot v=a\sin\theta \end{matrix}\right. θ(t)min​J=tf​s.t.{x˙=u, y˙​=vu˙=acosθ, v˙=asinθ​

已知初始点状态、落点位置、经过点的位置，即 x ( 0 ) = [ x ( 0 ) , y ( 0 ) , u ( 0 ) , v ( 0 ) ] T = 0 , N ( x ( t 1 ) , t 1 ) = [ x ( t 1 ) − x 1 y ( t 1 ) − y 1 ] = 0 ,   t 1 ∈ ( 0 , t f ) ψ ( x ( t f ) , t f ) = [ x ( t f ) − x f y ( t f ) ] = 0 \mathbf x(0)=[x(0),y(0),u(0),v(0)]^\mathrm T=0,\\ N(\mathbf x(t_1),t_1)=\begin{bmatrix}x(t_1)-x_1\\ y(t_1)-y_1\end{bmatrix}=0,\ t_1\in(0,t_f)\\ \psi(\mathbf x(t_f),t_f)=\begin{bmatrix}x(t_f)-x_f\\y(t_f)\end{bmatrix}=0 x(0)=[x(0),y(0),u(0),v(0)]T=0,N(x(t1​),t1​)=[x(t1​)−x1​y(t1​)−y1​​]=0, t1​∈(0,tf​)ψ(x(tf​),tf​)=[x(tf​)−xf​y(tf​)​]=0

且 t 1 t_1 t1​未知。求最优控制 θ ∗ ( t ) \theta^*(t) θ∗(t) 首先写出哈密尔顿函数 H = 1 + λ 1 u + λ 2 v + λ 3 a cos ⁡ θ + λ 4 a sin ⁡ θ H=1+\lambda_1u+\lambda_2v+\lambda_3a\cos\theta+\lambda_4a\sin\theta H=1+λ1​u+λ2​v+λ3​acosθ+λ4​asinθ，协态方程 λ ˙ ( t ) = − ∂ H ∂ x = [ 0 0 − λ 1 − λ 2 ] \dot\lambda(t)=-\frac {\partial H}{\partial \mathbf x}=\begin{bmatrix}0\\0\\ -\lambda_1\\-\lambda_2\end{bmatrix} λ˙(t)=−∂x∂H​=⎣ ⎡​00−λ1​−λ2​​⎦ ⎤​

控制方程 ∂ H ∂ θ = − λ 3 sin ⁡ θ + λ 4 a cos ⁡ θ = 0 ⇒ tan ⁡ θ ∗ = λ 4 λ 3 \frac{\partial H}{\partial \theta}=-\lambda_3\sin\theta+\lambda_4a\cos\theta=0\\\rArr\tan\theta^*=\frac{\lambda_4}{\lambda_3} ∂θ∂H​=−λ3​sinθ+λ4​acosθ=0⇒tanθ∗=λ3​λ4​​

可见只要求出协态变量就可以得到最优控制。对终端约束引入拉格朗日乘子 μ ∈ R 2 , Φ = ϕ + μ T ψ \mu\in\R^2,\Phi=\phi+\mu^\mathrm T\psi μ∈R2,Φ=ϕ+μTψ，终端约束与终端时间满足： λ ( t f ) = ∂ Φ ∂ x = [ μ 1 , μ 2 , 0 , 0 ] T H ( t f ) + ∂ Φ ∂ t f = 1 + μ 1 u ( t f ) + μ 2 v ( t f ) = 0 \lambda(t_f)=\frac{\partial\Phi}{\partial \mathbf x}=[\mu_1,\mu_2,0,0]^\mathrm T\\ H(t_f)+\frac{\partial \Phi}{\partial t_f}=1+\mu_1u(t_f)+\mu_2v(t_f)=0 λ(tf​)=∂x∂Φ​=[μ1​,μ2​,0,0]TH(tf​)+∂tf​∂Φ​=1+μ1​u(tf​)+μ2​v(tf​)=0

对内点约束引入拉格朗日乘子 π ∈ R 2 \pi\in\R^2 π∈R2，内点约束满足： λ ( t 1 − ) = λ ( t 1 + ) + π T ∂ N ∂ x \lambda(t_{1-})=\lambda(t_{1+})+\pi^\mathrm T\frac{\partial N}{\partial \mathbf x} λ(t1−​)=λ(t1+​)+πT∂x∂N​

推导可得 λ 1 − = λ 1 + + π 1 = μ 1 + π 1 λ 2 − = λ 2 + + π 2 = μ 2 + π 2 \lambda_{1-}=\lambda_{1+}+\pi_1=\mu_1+\pi_1\\ \lambda_{2-}=\lambda_{2+}+\pi_2=\mu_2+\pi_2\\ λ1−​=λ1+​+π1​=μ1​+π1​λ2−​=λ2+​+π2​=μ2​+π2​

λ 3 , 4 \lambda_{3,4} λ3,4​在 t 1 t_1 t1​处连续，且可得 θ ( t ) \theta(t) θ(t)连续。由于协态变量是分段的，在两个阶段都不变而 λ 1 , 2 \lambda_{1,2} λ1,2​只在 t 1 t_1 t1​处跳变，从 t f t_f tf​时刻往前推导可以得到 λ 1 ( t ) = { μ 1 + π 1 t ∈ [ 0 , t 1 ) μ 1 t ∈ ( t 1 , t f ] λ 2 ( t ) = { μ 2 + π 2 t ∈ [ 0 , t 1 ) μ 2 t ∈ ( t 1 , t f ] λ 3 ( t ) = { μ 1 t f + t 1 ( μ 1 + π 1 ) − ( 2 μ 1 + π 1 ) t t ∈ [ 0 , t 1 ) μ 1 ( t f − t ) t ∈ ( t 1 , t f ] λ 4 ( t ) = { μ 2 t f + t 1 ( μ 2 + π 2 ) − ( 2 μ 2 + π 2 ) t t ∈ [ 0 , t 1 ) μ 2 ( t f − t ) t ∈ ( t 1 , t f ] \lambda_1(t)=\begin{cases}\mu_1+\pi_1&t\in[0,t_1)\\ \mu_1&t\in(t_1,t_f]\end{cases}\\ \lambda_2(t)=\begin{cases}\mu_2+\pi_2&t\in[0,t_1)\\ \mu_2&t\in(t_1,t_f]\end{cases}\\ \lambda_3(t)= \begin{cases}\mu_1t_f+t_1(\mu_1+\pi_1)-(2\mu_1+\pi_1)t&t\in[0,t_1)\\ \mu_1(t_f-t)&t\in(t_1,t_f]\end{cases}\\ \lambda_4(t)= \begin{cases}\mu_2t_f+t_1(\mu_2+\pi_2)-(2\mu_2+\pi_2)t&t\in[0,t_1)\\ \mu_2(t_f-t)&t\in(t_1,t_f]\end{cases}\\ λ1​(t)={μ1​+π1​μ1​​t∈[0,t1​)t∈(t1​,tf​]​λ2​(t)={μ2​+π2​μ2​​t∈[0,t1​)t∈(t1​,tf​]​λ3​(t)={μ1​tf​+t1​(μ1​+π1​)−(2μ1​+π1​)tμ1​(tf​−t)​t∈[0,t1​)t∈(t1​,tf​]​λ4​(t)={μ2​tf​+t1​(μ2​+π2​)−(2μ2​+π2​)tμ2​(tf​−t)​t∈[0,t1​)t∈(t1​,tf​]​

另外，内点时间 H ( ⋅ ∗ , t ) H(\cdot^*,t) H(⋅∗,t)不连续，即 H ( ⋅ ∗ , t 1 − ) = H ( ⋅ ∗ , t 1 + ) − π T ∂ N ∂ t 1 ⇒ λ 1 − u ( t 1 ) + λ 2 − v ( t 1 ) = λ 1 + u ( t 1 ) + λ 2 + v ( t 1 ) ⇒ u ( t 1 ) π 1 = − v ( t 1 ) π 2 H(\cdot^*,t_{1-})=H(\cdot^*,t_{1+})-\pi^\mathrm T\frac{\partial N}{\partial t_{1}}\\ \rArr \lambda_{1-}u(t_1)+\lambda_{2-}v(t_1)=\lambda_{1+}u(t_1)+\lambda_{2+}v(t_1)\\ \rArr u(t_1)\pi_1=-v(t_1)\pi_2 H(⋅∗,t1−​)=H(⋅∗,t1+​)−πT∂t1​∂N​⇒λ1−​u(t1​)+λ2−​v(t1​)=λ1+​u(t1​)+λ2+​v(t1​)⇒u(t1​)π1​=−v(t1​)π2​

把以上这些条件代入解析表达式进行数值求解可得最优控制，由于计算比较复杂，后面的就忽略了。我按照直接法写了一个GPOPS程序，求解结果大概是这样，需要的同学可以在CSDN下载。

[1] 邢继祥. 最优控制应用基础[M]. 科学出版社, 2003. [2] Bryson A E , Ho Y C ,Applied optimal control : optimization, estimation, and control[J]. IEEE Transactions on Systems Man & Cybernetics, 1975 [3] Moritz Diehl, Numerical Optimal Control (draft), 2011 [4]沈红新. 基于解析同伦的月地应急返回轨迹优化方法[D].国防科学技术大学,2014.