| Weibull Distribution韦布尔分布的深入详述(3)分析案例建模实践 | 您所在的位置:网站首页 › 伽马分布应用场合 › Weibull Distribution韦布尔分布的深入详述(3)分析案例建模实践 |
Weibull Distribution韦布尔分布的深入详述(3)分析案例建模实践
|
前言:
前两个章节,我们对韦伯分布的分布函数,以及相关的曲线参数已经做了比较深入的了解,现在,我们结合统计的实际案例进行分析,这样有助于我们应用于工程实践和理解参数的最终意义。 本章我们针对实际的分析案例进行分析。 包括:真空吸尘器的生命周期、移动硬盘、轮胎的使用里程 实例和参数 例一:真空吸尘器的生命周期定义某个品牌的真空吸尘器生命周期 X (单位:百工作小时)具备韦伯分布,而且他的历史数据可知有,β =2,η=3,求: E ( X ) a n d V ( X ) E(X) and V(X) E(X)andV(X) E ( X ) = η Γ ( 1 β + 1 ) = 3 Γ ( 1 2 + 1 ) = 3 Γ ( 3 / 2 ) = 3 × 1 2 Γ ( 1 / 2 ) = 3 2 × π = 3 2 × 1.7725 = 2.6587 \begin{aligned} E(X) &= \eta \Gamma (\dfrac{1}{\beta}+1)\\ &=3\Gamma(\dfrac{1}{2}+1)\\ &=3\Gamma(3/2)\\ &=3\times\dfrac{1}{2}\Gamma(1/2)\\ &=\dfrac{3}{2}\times\sqrt{\pi}\\ &=\dfrac{3}{2}\times1.7725\\ &=2.6587 \end{aligned} E(X)=ηΓ(β1+1)=3Γ(21+1)=3Γ(3/2)=3×21Γ(1/2)=23×π =23×1.7725=2.6587 【案,意义为:吸尘器平均工作寿命为265.8小时】 V ( X ) = η 2 [ Γ ( 2 β + 1 ) − ( Γ ( 1 β + 1 ) ) 2 ] = 3 2 [ Γ ( 2 2 + 1 ) − ( Γ ( 1 2 + 1 ) ) 2 ] = 9 [ Γ ( 2 ) − ( Γ ( 3 / 2 ) ) 2 ] = 9 [ 1 − ( 1 2 Γ ( 1 / 2 ) ) 2 ] = 9 [ 1 − ( π 2 ) 2 ] = 9 [ 1 − ( 3.1416 2 ) 2 ] = 1.931846 \begin{aligned} V(X) &= \eta^2 \bigg[\Gamma (\dfrac{2}{\beta}+1) -\bigg(\Gamma (\dfrac{1}{\beta}+1) \bigg)^2\bigg]\\ &=3^2 \bigg[\Gamma (\dfrac{2}{2}+1) -\bigg(\Gamma (\dfrac{1}{2}+1) \bigg)^2\bigg]\\ &=9\bigg[\Gamma(2)-\big(\Gamma(3/2)\big)^2\bigg]\\ &=9\bigg[1-\bigg(\frac{1}{2}\Gamma(1/2)\bigg)^2\bigg]\\ &=9\bigg[1-\bigg(\frac{\sqrt{\pi}}{2}\bigg)^2\bigg]\\ &=9\bigg[1-\bigg(\frac{\sqrt{3.1416}}{2}\bigg)^2\bigg]\\ &=1.931846 \end{aligned} V(X)=η2[Γ(β2+1)−(Γ(β1+1))2]=32[Γ(22+1)−(Γ(21+1))2]=9[Γ(2)−(Γ(3/2))2]=9[1−(21Γ(1/2))2]=9[1−(2π )2]=9[1−(23.1416 )2]=1.931846 【案,在第一章我们已经分析过V(X)的意义,通过这个实例我们看到,吸尘器的平均使用寿命,如果用V(X)来分析的话,要不纯均值要小一点,可是,吸尘器商家一般都会在产品说明书上写上数学期望E(X)的值,我们使用者可以用这个值进行参考】 下面是计算吸尘器在不同的百小时工作范围内发生故障的概率: 【小于600小时的故障概率是98%】 P ( X ≤ 6 ) P(X\leq 6) P(X≤6) P ( X ≤ 6 ) = F ( 6 ) = 1 − e − ( 6 / 3 ) 2 = 1 − e − ( 2 ) 2 = 1 − e − ( 4 ) = 1 − 0.0183 = 0.9817 \begin{aligned} P(X\leq 6) &=F(6)\\ &= 1-e^{-(6/3)^{2}}\\ &= 1-e^{-(2)^{2}}\\ &= 1-e^{-(4)}\\ &=1-0.0183\\ &=0.9817 \end{aligned} P(X≤6)=F(6)=1−e−(6/3)2=1−e−(2)2=1−e−(4)=1−0.0183=0.9817 【180小时到500小时之间的故障概率是67%】 P ( 1.8 ≤ X ≤ 5 ) P(1.8\leq X \leq 5) P(1.8≤X≤5) P ( 1.8 ≤ X ≤ 6 ) = F ( 6 ) − F ( 1.8 ) = [ 1 − e − ( 6 / 3 ) 2 ] − [ 1 − e − ( 1.8 / 3 ) 2 ] = e − ( 0.6 ) 2 − e − ( 2 ) 2 = e − ( 0.36 ) − e − ( 4 ) = 0.6977 − 0.0183 = 0.6794 \begin{aligned} P(1.8 \leq X\leq 6) &=F(6)-F(1.8)\\ &= \bigg[1-e^{-(6/3)^{2}}\bigg] -\bigg[1-e^{-(1.8/3)^{2}}\bigg]\\ &= e^{-(0.6)^{2}}-e^{-(2)^{2}}\\ &= e^{-(0.36)}-e^{-(4)}\\ &=0.6977-0.0183\\ &=0.6794 \end{aligned} P(1.8≤X≤6)=F(6)−F(1.8)=[1−e−(6/3)2]−[1−e−(1.8/3)2]=e−(0.6)2−e−(2)2=e−(0.36)−e−(4)=0.6977−0.0183=0.6794 【大于300小时的故障概率是36.7%】 P ( X ≥ 3 ) P(X\geq 3) P(X≥3)
P
(
X
≥
3
)
=
1
−
P
(
X
<
3
)
=
1
−
F
(
3
)
=
1
−
[
1
−
e
−
(
3
/
3
)
2
]
=
e
−
(
1
)
2
=
0.3679
\begin{aligned} P(X\geq 3) &=1-P(X< 3)\\ &= 1-F(3)\\ &= 1-\bigg[1-e^{-(3/3)^{2}}\bigg]\\ &= e^{-(1)^{2}}\\ &=0.3679 \end{aligned}
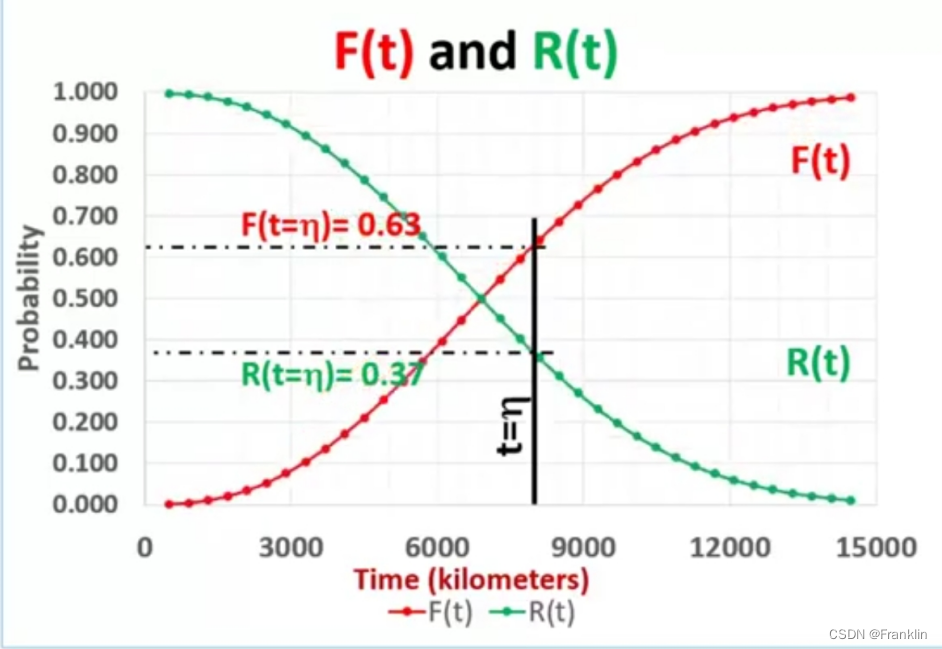
P(X≥3)=1−P(X0) (1)
F(t)=1−e−(ηt)β(t>0)(1) 而可靠性为:
R
(
t
)
=
e
−
(
t
η
)
β
(
t
>
0
)
(
2
)
\large\displaystyle R(t) = e^{-(\frac{t}{\eta })^{\beta }} (t>0) (2)
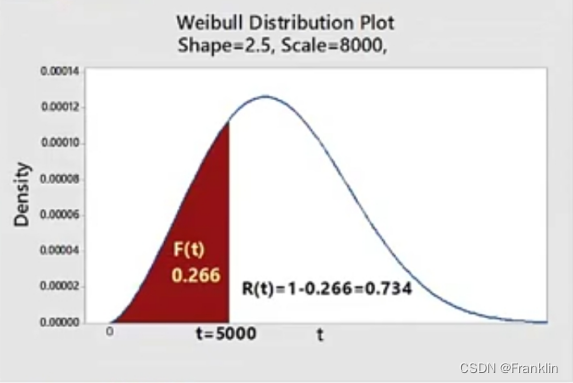
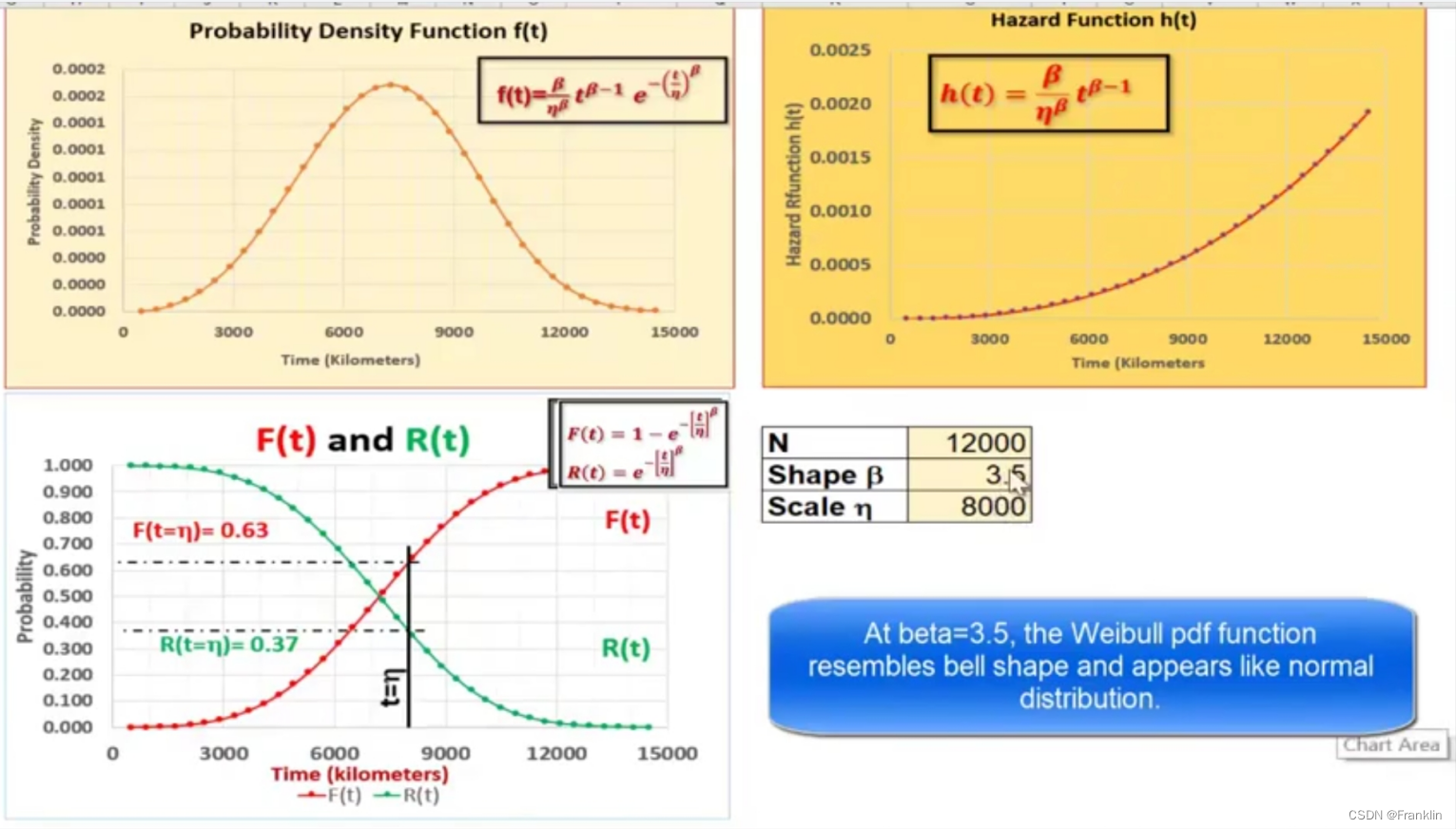
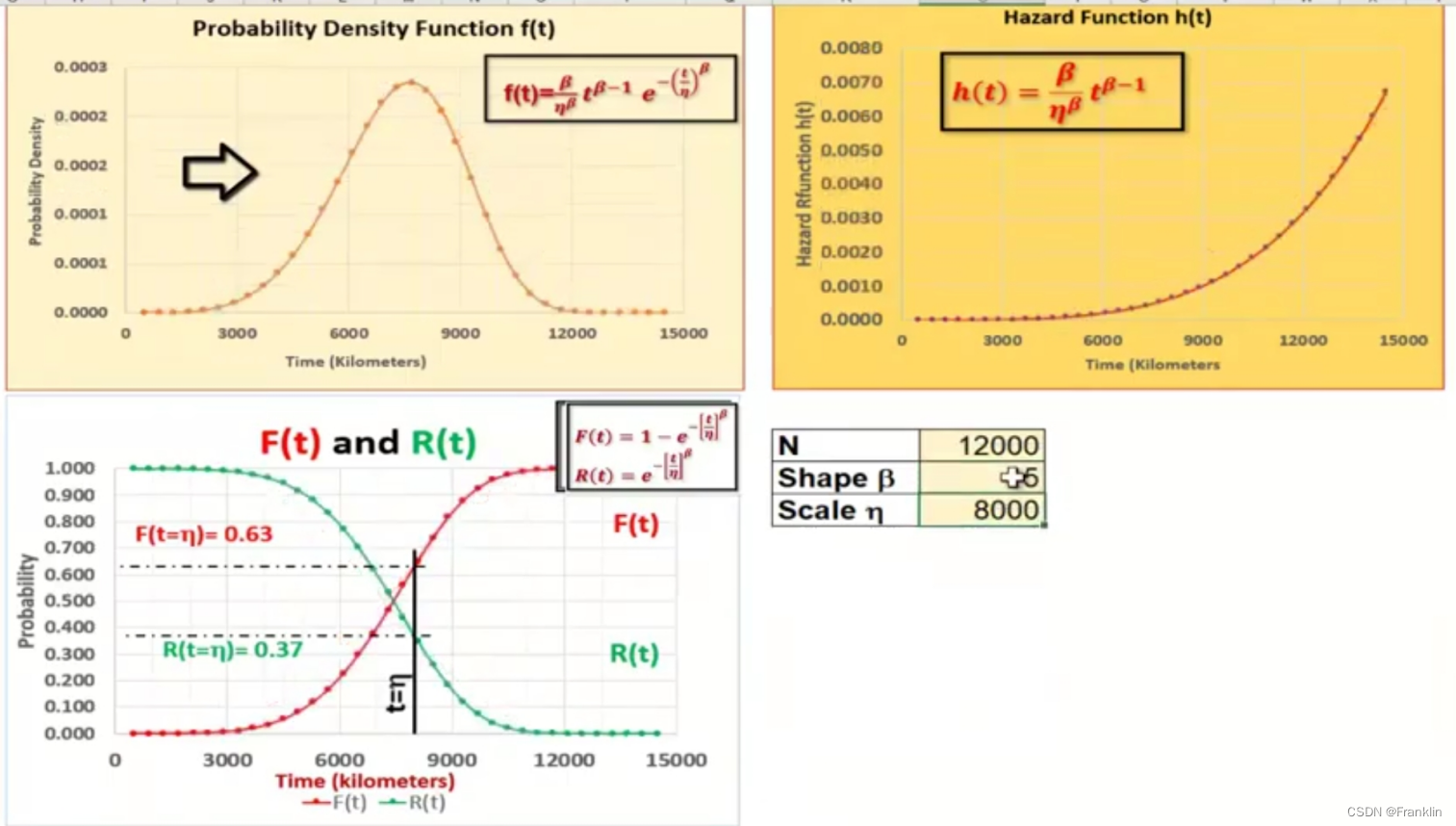
R(t)=e−(ηt)β(t>0)(2) 我们可以画出韦伯分布的图形如下: 12000 * 0.266 = 3188 也就是在5000公里的时候,大约有3188条轮胎会出现问题。 h(t)失效函数稳定随着时间增加而指数增加。我们知道之前轮胎实际的统计数据,η =8000时候,β=3.5,那么为什么是β=3.5? 这里大约可解释为,轮胎的磨损的模型比较接近于高斯分布,也就是normal distribution,也就是轮胎的使用寿命,磨损的程度虽然和路况有关系,但是,统计的数据表述,最相关的还是轮胎本身的特性,例如橡胶材料,轮胎大小来决定的。这样就是高斯分布的样子。而8000公里也许就是轮胎的设计寿命时间。
【也许轮胎厂商希望轮胎使用,8000公里就必须立即更换,那么,也许设计轮胎让他数据统计达到β=8,这样如箭头所示,在8000公里的时候,h(t)的故障会急剧上升,而8000公里之前,他可以保证安全,这也许就是研究韦伯分布的实际意义】 第1章 第2章 |
【本文地址】
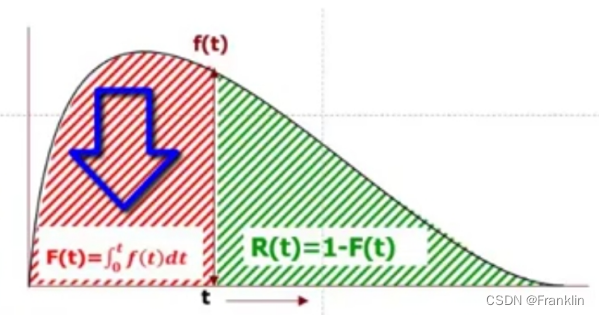 依据已知题意,代入公式(1),β=2.5,η =8000公里,t=5000公里,有,
依据已知题意,代入公式(1),β=2.5,η =8000公里,t=5000公里,有,