【运筹优化】网络最大流问题及三种求解算法详解 + Python代码实现

您所在的位置：网站首页 › 优化运筹学 › 【运筹优化】网络最大流问题及三种求解算法详解 + Python代码实现

【运筹优化】网络最大流问题及三种求解算法详解 + Python代码实现

2024-07-15 04:58| 来源: 网络整理| 查看: 265

文章目录一、网络最大流问题二、Ford-Fulkerson 算法（最坏时间复杂度：O(f×m)）2.1 残存网络2.2 增广路径2.3 算法介绍2.4 完整代码三、Edmons-Karp 算法（最坏时间复杂度：O(m×m×n)）3.1 算法介绍3.2 完整代码四、Dinic 算法（最坏时间复杂度：O(m×n×n)）4.1 Level Graph4.2 算法介绍4.3 完整代码五、三种算法的性能测试5.1 测试15.2 测试25.3 测试部分完整代码5.4 结论（仅供参考）

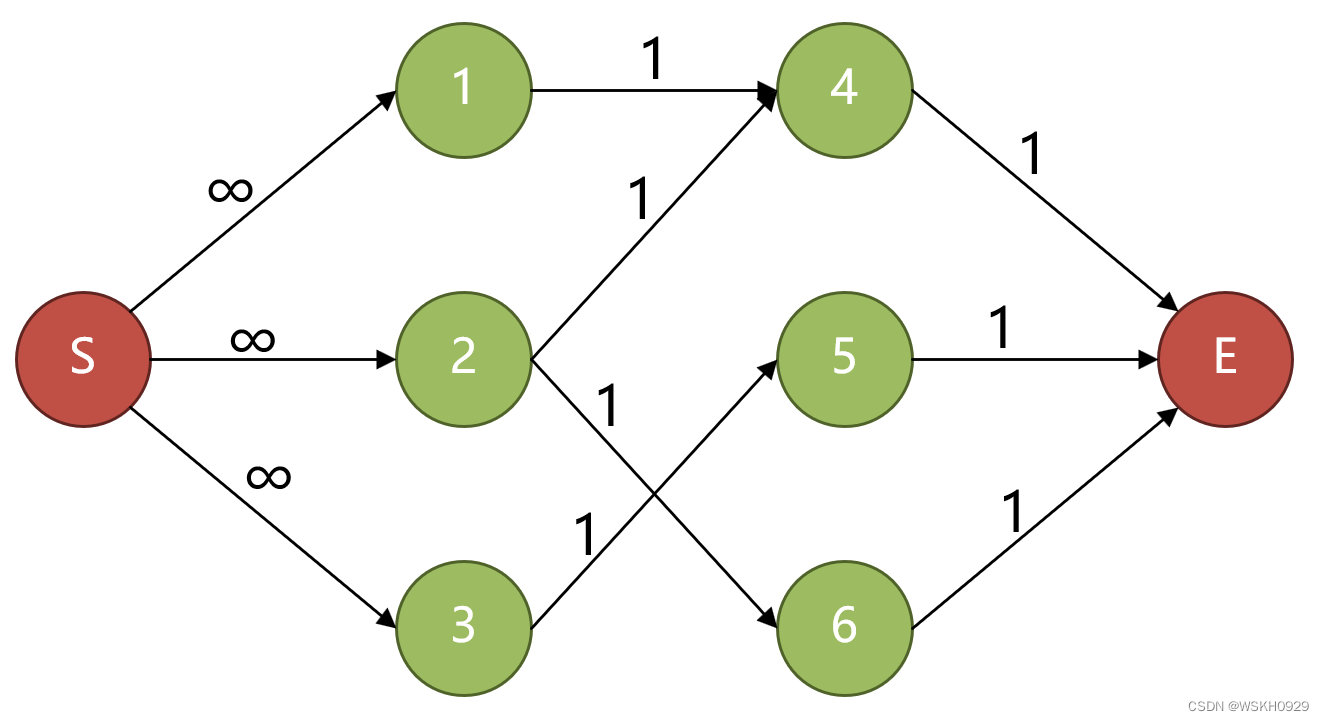
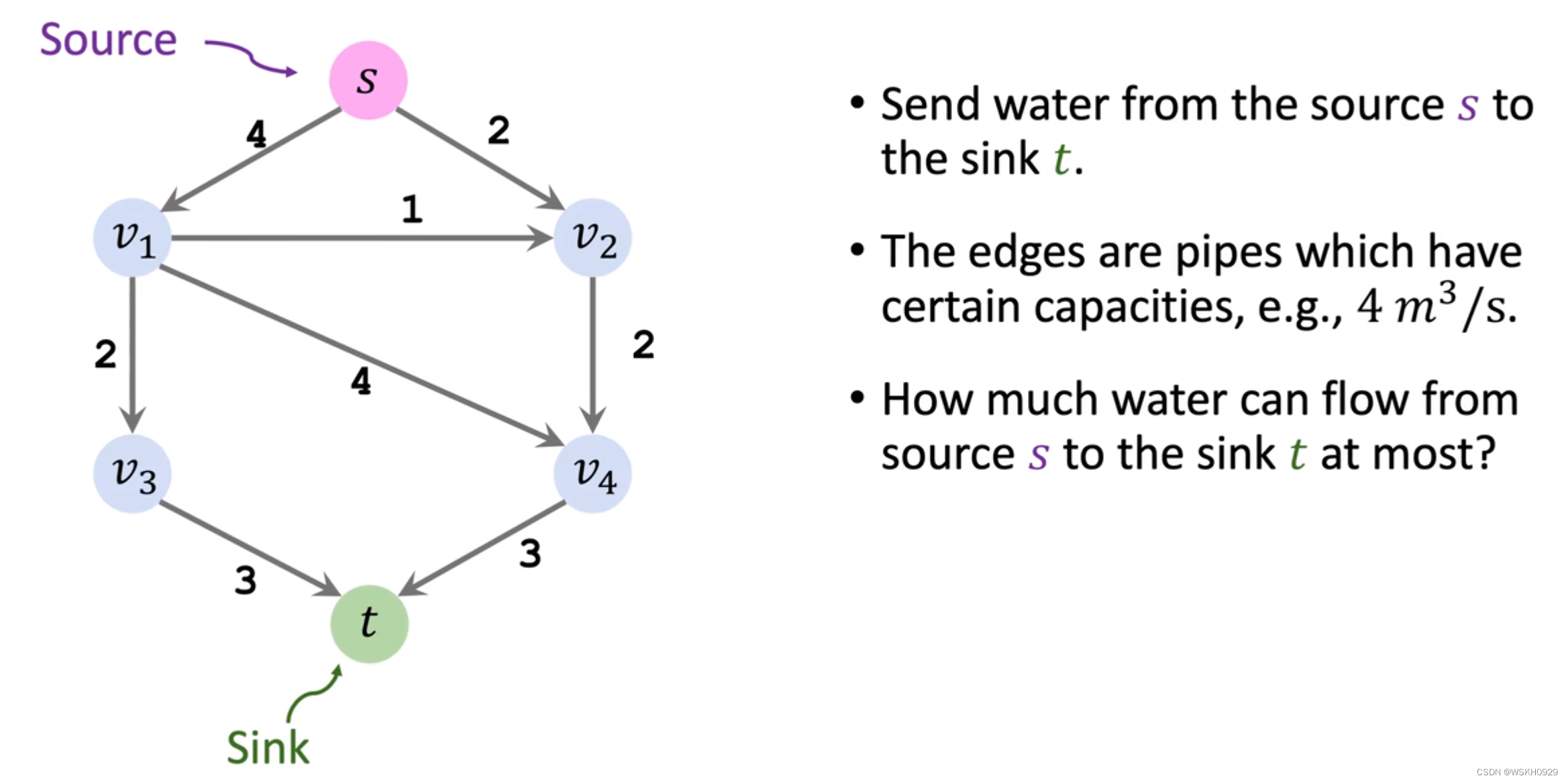
标题中时间复杂度用到的符号说明：f 代表最大流的大小，m代表边的数量，n 代表节点的数量本博客学习自：B站-ShusenWang

一、网络最大流问题

最大流问题，是网络流理论研究的一个基本问题，求网络中一个可行流 f ∗ f* f∗，使其流量 v ( f ) v(f) v(f)达到最大，这种流 f f f 称为最大流，这个问题称为 (网络)最大流问题。

最大流问题是一个特殊的线性规划问题，就是在容量网络中，寻找流量最大的可行流。

下面我们用一个例子来直观理解网络最大流问题

如下图所示，S处是一个水源，图中的弧是水管，管道由于材质、直径的不同，其所能承受的输水量也不同，所以就出现了下图所示的不同数值的弧，我们的目标是将水源从 S 通过管道运输到 T 点，且在满足管道能承受的输水量的前提下尽可能使得输送到 T 点的水最大化。

这就是最大流问题。

在这里插入图片描述

二、Ford-Fulkerson 算法（最坏时间复杂度：O(f×m)） 2.1 残存网络

残存网络其实就是用边的剩余容量来表示每条边，如下图所示的残存网络。S->v2这条边上的数字“2”代表这条边剩余可通过容量为2。

实际写代码只用残存网络即可求出最大流

在这里插入图片描述

2.2 增广路径

一条能从起点S到达起点T的流量大于0的路径就被称为增广路径，通过增广路径，流量一定会增加。

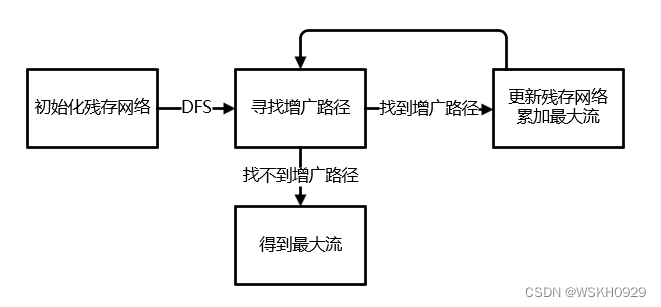
在这里插入图片描述

2.3 算法介绍

该算法概况起来，就是在残存网络中不断寻找增广路径，每找到一条增广路径，就递增最大流 f f f，并更新残存网络，直到残存网络中不存在增广路径，则此时f即为最终的最大流。

Ford-Fulkerson 算法是通过 DFS（深度优先遍历）的方式在当前残存网络中寻找增广路径的。

根据木桶原理，增广路径的流量等于该路径的边的最小剩余流量。如下图所示的增广路径，它的流量就是3，因为 v4->t 的容量为3

在这里插入图片描述在找到增广路径后，我们要更新残存网络。首先就是对该增广路径的正向边进行更新，将正向边的剩余流量全部减去3

在这里插入图片描述

然后对该增广路径的反向边进行更新（反向边在初始化的时候，剩余流量都为0，所以在上面的图中没有画出来，反向边的作用就是让算法可以反悔，从而通过多次迭代，找到最优解），反向边的剩余流量全部加上3

在这里插入图片描述添加反向边是这一算法能够精确求解最大流问题的基础保障

然后重复上述过程，直到找不到增广路径，算法结束

Ford-Fulkerson 算法的整体实现思路如下，其实就是不断从残存网络寻找增广路径的过程

在这里插入图片描述

2.4 完整代码

完整代码

# -*- coding: utf-8 -*-# # Author: WSKH # Blog: wskh0929.blog.csdn.net # Time: 2023/2/13 9:45 # Description: Ford Fulkerson 算法求解最大流问题 class Node: def __init__(self, name, arc_dict): self.name = name self.arc_dict = arc_dict def create_node(name, next_list, flow_list): arc_dict = {} for i in range(len(next_list)): arc_dict[next_list[i]] = flow_list[i] return Node(name, arc_dict) def Ford_Fulkerson_Solve(s, e, node_list, name_index_dict): ''' Ford_Fulkerson 算法核心函数 :param s: 起始节点名称 :param e: 终止节点名称 :param node_list: 节点列表 :param name_index_dict: 节点名字和索引字典 :return: 返回搜索到的所有增广路径及其流值 ''' routes = [] while True: res = dfs(e, [s], None, node_list, name_index_dict) if res is None: return routes # 追加增广路径到routes routes.append(res) # 更新node_list route, flow = res for i in range(len(route) - 1): n1 = node_list[name_index_dict[route[i]]] n2 = node_list[name_index_dict[route[i + 1]]] # 正向更新 n1 -> n2 剩余流量减少 if n2.name in n1.arc_dict.keys() and n1.arc_dict[n2.name] is not None: n1.arc_dict[n2.name] = n1.arc_dict[n2.name] - flow # 反向更新 n2 -> n1 剩余流量增加 if n1.name in n2.arc_dict.keys() and n2.arc_dict[n1.name] is not None: n2.arc_dict[n1.name] = n2.arc_dict[n1.name] + flow def dfs(e, cur_route, last_flow, node_list, name_index_dict): ''' DFS搜索增广路径 :param e: 终点节点名称 :param cur_route: 当前路径 :param last_flow: 上一个节点的流值，用来计算最小流 :param node_list: 节点列表 :param name_index_dict: 节点名字和索引字典 :return: 返回搜索到的增广路径及其流值，如果没找到就返回 None ''' if cur_route[-1] == e: return cur_route, last_flow index = name_index_dict[cur_route[-1]] for next_node_name in node_list[index].arc_dict.keys(): if next_node_name not in cur_route: flow = node_list[index].arc_dict[next_node_name] if flow is None or flow > 0: cur_route.append(next_node_name) res = dfs(e, cur_route, min_flow(last_flow, flow), node_list, name_index_dict) if res is not None: return res cur_route.pop(-1) def min_flow(f1, f2): ''' 求两个流量的较小者 ''' if f1 is None: return f2 elif f2 is None: return f1 else: return min(f1, f2) if __name__ == '__main__': # 格式: [节点名, 后继节点的名称, 当前节点到各个后继的流量] （None 代表流量无穷大） graph = [ ["S", ["1", "2", "3"], [None, None, None]], ["1", ["4"], [1]], ["2", ["4", "6"], [1, 1]], ["3", ["5"], [1]], ["4", ["1", "2", "E"], [0, 0, 1]], ["5", ["3", "E"], [0, 1]], ["6", ["2", "E"], [0, 1]], ["E", [], []] ] name_index_dict = dict() node_list = [] for i in range(len(graph)): node_list.append(create_node(graph[i][0], graph[i][1], graph[i][2])) name_index_dict[graph[i][0]] = i # 调用算法求解最大流 routes = Ford_Fulkerson_Solve("S", "E", node_list, name_index_dict) for i, (route, flow) in enumerate(routes): print(f"Route-{i + 1}: {route} , flow: {flow}")

测试案例

在这里插入图片描述

程序输出

Route-1: ['S', '1', '4', 'E'] , flow: 1 Route-2: ['S', '2', '6', 'E'] , flow: 1 Route-3: ['S', '3', '5', 'E'] , flow: 1 三、Edmons-Karp 算法（最坏时间复杂度：O(m×m×n)） 3.1 算法介绍

Edmons-Karp 算法比 Ford-Fulkerson 算法晚16年提出，它和 Ford-Fulkerson 算法唯一的区别在于寻找增广路径的方式不同，其余步骤完全一样。Edmons-Karp 算法在寻找增广路的时候是将残存网络看作一个无权图然后求S到T的最短路，这条最短路上的最小剩余流量如果大于0，那么就作为增广路径，进行残存网络的更新。

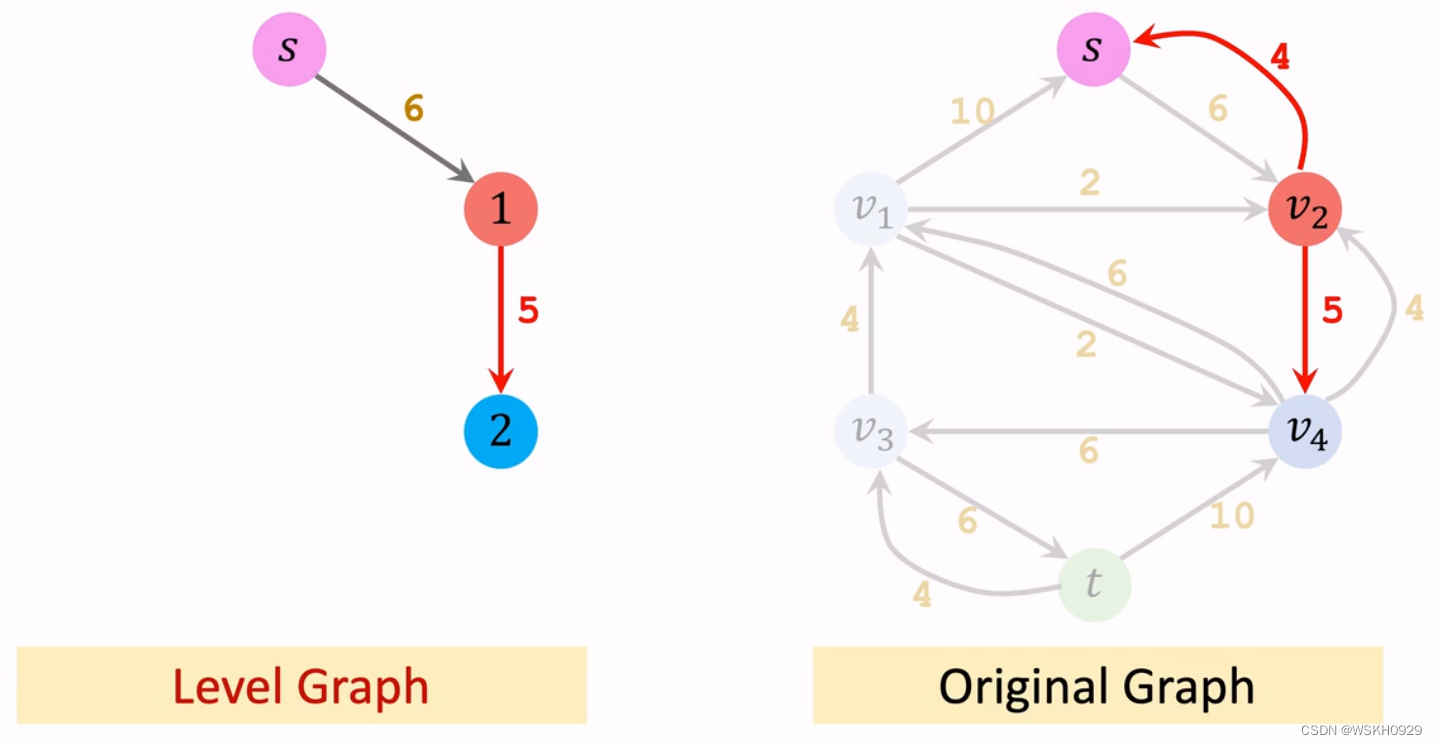
在这里插入图片描述

Edmons-Karp 算法贡献在于，它具有比 Ford-Fulkerson 算法更小的时间复杂度，Ford-Fulkerson 算法的时间复杂度受最大流大小影响，而 Edmons-Karp 算法只受节点数量和边的数量的影响

3.2 完整代码

本代码使用 BFS（广度优先搜索）求最短路，测试案例还是和上面的一样

# -*- coding: utf-8 -*-# # Author: WSKH # Blog: wskh0929.blog.csdn.net # Time: 2023/2/13 11:54 # Description: Edmons Karp 算法求解最大流问题 from queue import PriorityQueue class Node: def __init__(self, name, arc_dict): self.name = name self.arc_dict = arc_dict class Label: def __init__(self, route, last_flow): self.route = route self.last_flow = last_flow def __lt__(self, o): if len(self.route) == len(o.route): return 0 else: return 1 if len(self.route) > len(o.route) else -1 def create_node(name, next_list, flow_list): arc_dict = {} for i in range(len(next_list)): arc_dict[next_list[i]] = flow_list[i] return Node(name, arc_dict) def Edmons_Karp_Solve(s, e, node_list, name_index_dict): ''' Edmons Karp 算法核心函数 :param s: 起始节点名称 :param e: 终止节点名称 :param node_list: 节点列表 :param name_index_dict: 节点名字和索引字典 :return: 返回搜索到的所有增广路径及其流值 ''' routes = [] while True: res = bfs(s, e, node_list, name_index_dict) if res is None: return routes # 追加增广路径到routes routes.append([res.route, res.last_flow]) # 更新node_list route, flow = res.route, res.last_flow for i in range(len(route) - 1): n1 = node_list[name_index_dict[route[i]]] n2 = node_list[name_index_dict[route[i + 1]]] # 正向更新 n1 -> n2 剩余流量减少 if n2.name in n1.arc_dict.keys() and n1.arc_dict[n2.name] is not None: n1.arc_dict[n2.name] = n1.arc_dict[n2.name] - flow # 反向更新 n2 -> n1 剩余流量增加 if n1.name in n2.arc_dict.keys() and n2.arc_dict[n1.name] is not None: n2.arc_dict[n1.name] = n2.arc_dict[n1.name] + flow def bfs(s, e, node_list, name_index_dict): queue = PriorityQueue() queue.put(Label([s], None)) while queue.empty() is False: res = queue.get() index = name_index_dict[res.route[-1]] for next_node_name in node_list[index].arc_dict.keys(): if next_node_name not in res.route: flow = node_list[index].arc_dict[next_node_name] if flow is None or flow > 0: route = res.route.copy() route.append(next_node_name) if next_node_name == e: return Label(route, min_flow(res.last_flow, flow)) queue.put(Label(route, min_flow(res.last_flow, flow))) def min_flow(f1, f2): ''' 求两个流量的较小者 ''' if f1 is None: return f2 elif f2 is None: return f1 else: return min(f1, f2) if __name__ == '__main__': # 格式: [节点名, 后继节点的名称, 当前节点到各个后继的流量] （None 代表流量无穷大） graph = [ ["S", ["1", "2", "3"], [None, None, None]], ["1", ["4"], [1]], ["2", ["4", "6"], [1, 1]], ["3", ["5"], [1]], ["4", ["1", "2", "E"], [0, 0, 1]], ["5", ["3", "E"], [0, 1]], ["6", ["2", "E"], [0, 1]], ["E", [], []] ] name_index_dict = dict() node_list = [] for i in range(len(graph)): node_list.append(create_node(graph[i][0], graph[i][1], graph[i][2])) name_index_dict[graph[i][0]] = i # 调用算法求解最大流 routes = Edmons_Karp_Solve("S", "E", node_list, name_index_dict) for i, (route, flow) in enumerate(routes): print(f"Route-{i + 1}: {route} , flow: {flow}")

程序输出

Route-1: ['S', '1', '4', 'E'] , flow: 1 Route-2: ['S', '2', '6', 'E'] , flow: 1 Route-3: ['S', '3', '5', 'E'] , flow: 1 四、Dinic 算法（最坏时间复杂度：O(m×n×n)）

由于边的数量 m 通常远远大于节点数量 n，所以通常情况下 Dinic 算法比 Edmons-Karp 算法更快。而且 Dinic 算法发表时间比 Edmons-Karp 算法还要早两年。

为了更好的讲解 Dinic 算法，下面先介绍一个重要的概念 Level Graph

4.1 Level Graph

Level Graph 是原图的一个子图，保留了原图中的所有节点和一部分边，下面图解 Level Graph 的构造过程

首先，将 S 作为 Level Graph 的第零层

在这里插入图片描述

然后，从 S 出发，可以到达的点有 v2，将 v2 加入 Level Graph，记作第一层，保留第零层到第一层的边

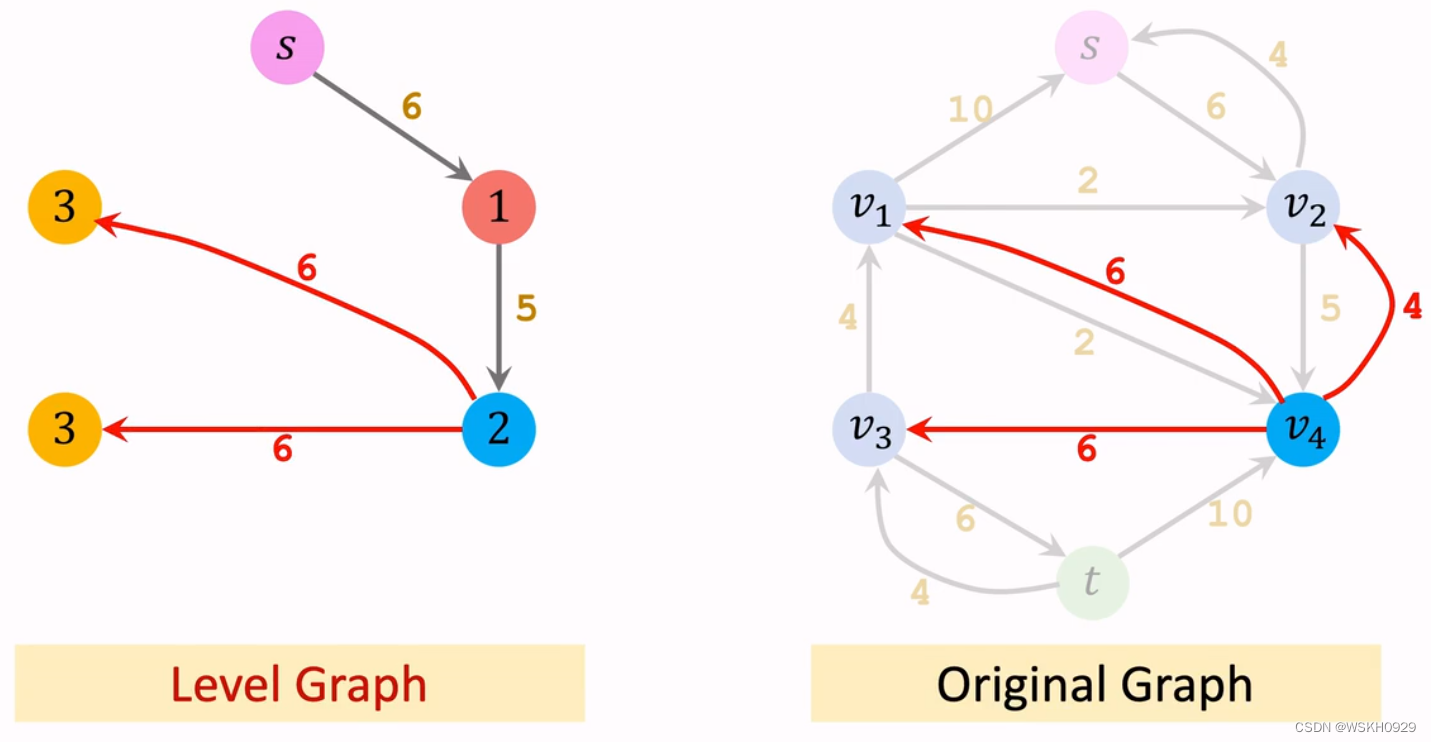
在这里插入图片描述

看一下右边的原图，从第一层可以到达的节点有 S 和 v4，由于 S 已经在 Level Graph 中了，所以不考虑。将 v4 加入 Level Graph，记作第二层，保留第一层到第二层的边。

在这里插入图片描述

看一下右边的原图，从第二层可以到达的节点有 v1、v2和v3，由于 v2 已经在 Level Graph中了，所以只考虑 v1和v3，将它们加入 Level Graph，记作第三层，保留第二层到第三层的边

在这里插入图片描述

看一下右边的原图，从第三层可以到达所有节点，由于目前只剩下节点 t 没有加入 Level Graph，所以将 t 加入 Level Graph，记作第四层，保留第三层到第四层的边。

在这里插入图片描述

至此，原图的 Level Graph 构造完毕！Level Graph 中节点的层数代表着从起点到达该起点所需要的最少步数（其实就是无权图下的最短路），这么看来，Dinic 算法其实结合了 Ford-Filkerson 和 Edmons-Karp 两个算法的思想呀！

4.2 算法介绍

介绍完 Level Graph，下面开始正式介绍 Dinic 算法！

在这里插入图片描述

4.3 完整代码 # -*- coding: utf-8 -*-# # Author: WSKH # Blog: wskh0929.blog.csdn.net # Time: 2023/2/13 19:26 # Description: Dinic 算法求解最大流问题 import numpy as np class Node: def __init__(self, name, arc_dict): self.name = name self.arc_dict = arc_dict def create_node(name, next_list, flow_list): arc_dict = {} for i in range(len(next_list)): arc_dict[next_list[i]] = flow_list[i] return Node(name, arc_dict) def create_level_graph(s, e, node_list, name_index_dict): level_graph = np.zeros((len(node_list), len(node_list))).tolist() cur_layer = [s] all_node = set() all_node.add(s) next_layer = set() while len(cur_layer) > 0: for node_name in cur_layer: node = node_list[name_index_dict[node_name]] for key in node.arc_dict.keys(): if key not in all_node and (node.arc_dict[key] is None or node.arc_dict[key] > 0): level_graph[name_index_dict[node_name]][name_index_dict[key]] = node.arc_dict[key] next_layer.add(key) all_node.add(key) cur_layer = list(next_layer) next_layer = set() return level_graph if e in all_node else None def Dinic_Solve(s, e, node_list, name_index_dict): routes = [] s_index = name_index_dict[s] e_index = name_index_dict[e] level_graph = create_level_graph(s, e, node_list, name_index_dict) while level_graph is not None: res_list = [] while True: res = dfs(e_index, [s_index], None, level_graph) if res is None: break # 更新 level graph route, flow = res for i in range(len(route) - 1): if level_graph[route[i]][route[i + 1]] is not None: level_graph[route[i]][route[i + 1]] -= flow # 追加记录增广路径 res_list.append(res) routes.append([[node_list[n].name for n in res[0]], res[1]]) # 更新残存网络 for res in res_list: update(res, node_list) # 重新构造 level graph level_graph = create_level_graph(s, e, node_list, name_index_dict) return routes def update(res, node_list): route, flow = res for i in range(len(route) - 1): n1 = node_list[route[i]] n2 = node_list[route[i + 1]] # 正向更新 n1 -> n2 剩余流量减少 if n2.name in n1.arc_dict.keys() and n1.arc_dict[n2.name] is not None: n1.arc_dict[n2.name] = n1.arc_dict[n2.name] - flow # 反向更新 n2 -> n1 剩余流量增加 if n1.name in n2.arc_dict.keys() and n2.arc_dict[n1.name] is not None: n2.arc_dict[n1.name] = n2.arc_dict[n1.name] + flow def dfs(e_index, cur_route, last_flow, level_graph): if cur_route[-1] == e_index: return cur_route, last_flow for next_node in range(len(level_graph)): if next_node not in cur_route: if level_graph[cur_route[-1]][next_node] is None or level_graph[cur_route[-1]][next_node] > 0: flow = min_flow(level_graph[cur_route[-1]][next_node], last_flow) cur_route.append(next_node) res = dfs(e_index, cur_route, flow, level_graph) if res is not None: return res cur_route.pop(-1) def min_flow(f1, f2): ''' 求两个流量的较小者 ''' if f1 is None: return f2 elif f2 is None: return f1 else: return min(f1, f2) if __name__ == '__main__': # 格式: [节点名, 后继节点的名称, 当前节点到各个后继的流量] （None 代表流量无穷大） graph = [ ["S", ["1", "2", "3"], [None, None, None]], ["1", ["4"], [1]], ["2", ["4", "6"], [1, 1]], ["3", ["5"], [1]], ["4", ["1", "2", "E"], [0, 0, 1]], ["5", ["3", "E"], [0, 1]], ["6", ["2", "E"], [0, 1]], ["E", [], []] ] name_index_dict = dict() node_list = [] for i in range(len(graph)): node_list.append(create_node(graph[i][0], graph[i][1], graph[i][2])) name_index_dict[graph[i][0]] = i # 调用算法求解最大流 routes = Dinic_Solve("S", "E", node_list, name_index_dict) for i, (route, flow) in enumerate(routes): print(f"Route-{i + 1}: {route} , flow: {flow}")

程序输出

Route-1: ['S', '3', '5', 'E'] , flow: 1 Route-2: ['S', '1', '4', 'E'] , flow: 1 Route-3: ['S', '2', '6', 'E'] , flow: 1 五、三种算法的性能测试

本节测试所用的案例是随机案例，如下图所示，根据指定的 m 和 n，构造一个中间有两层节点的网络图

在这里插入图片描述

5.1 测试1

在测试1中，固定 m = 10，n 从 2 开始以 1 的步长一直自增到 20

在这里插入图片描述

5.2 测试2

在测试2中，固定 n = 10，m 从 2 开始以 1 的步长一直自增到 20

在这里插入图片描述

5.3 测试部分完整代码 # -*- coding: utf-8 -*-# # Author: WSKH # Blog: wskh0929.blog.csdn.net # Time: 2023/2/13 15:23 # Description: import time import random from matplotlib import pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 #有中文出现的情况，需要u'内容' from EdmonsKarp import Edmons_Karp_Solve from FordFulkerson import Ford_Fulkerson_Solve from Dinic import Dinic_Solve from copy import deepcopy class Node: def __init__(self, name, arc_dict): self.name = name self.arc_dict = arc_dict def create_node(name, next_list, flow_list): arc_dict = {} for i in range(len(next_list)): arc_dict[next_list[i]] = flow_list[i] return Node(name, arc_dict) def create_instance(m, n, seed=666): random.seed(seed) S = "S" E = "E" node_list = [] name_index_dict = {} name_index_dict["S"] = 0 name_index_dict["E"] = m + n + 1 for i in range(m + n): name_index_dict[str(i + 1)] = i + 1 # 构造起点 node_list.append(create_node("S", [str(i + 1) for i in range(m)], [random.randint(800, 1200) for _ in range(m)])) # 构造第一层 for i in range(m): node_list.append( create_node(str(i + 1), [str(i + j + 2) for j in range(n)], [random.randint(800, 1200) for _ in range(n)])) # 构造第二层 for i in range(n): next_list = ["E"] flow_list = [random.randint(800, 1200)] for j in range(m): next_list.append(str(j + 1)) flow_list.append(0) node_list.append(create_node(str(m + i + 1), next_list, flow_list)) # 构造终点 node_list.append(create_node("E", [], [])) return S, E, node_list, name_index_dict def test1(): m = 10 n_arr = [i for i in range(1, 21, 1)] time_dict = { "Ford-Fulkerson": [], "Edmons-Karp": [], "Dinic": [] } for n in n_arr: instance = create_instance(m, n) S, E, node_list, name_index_dict = deepcopy(instance) start_time = time.time() Ford_Fulkerson_Solve(S, E, node_list, name_index_dict) time_dict["Ford-Fulkerson"].append(time.time() - start_time) S, E, node_list, name_index_dict = deepcopy(instance) start_time = time.time() Edmons_Karp_Solve(S, E, node_list, name_index_dict) time_dict["Edmons-Karp"].append(time.time() - start_time) S, E, node_list, name_index_dict = deepcopy(instance) start_time = time.time() Dinic_Solve(S, E, node_list, name_index_dict) time_dict["Dinic"].append(time.time() - start_time) plot(time_dict, n_arr, "固定m为10，n与运行时间的关系", "n") def test2(): n = 10 m_arr = [i for i in range(1, 21, 1)] time_dict = { "Ford-Fulkerson": [], "Edmons-Karp": [], "Dinic": [] } for m in m_arr: print(m) instance = create_instance(m, n) S, E, node_list, name_index_dict = deepcopy(instance) start_time = time.time() Ford_Fulkerson_Solve(S, E, node_list, name_index_dict) time_dict["Ford-Fulkerson"].append(time.time() - start_time) S, E, node_list, name_index_dict = deepcopy(instance) start_time = time.time() Edmons_Karp_Solve(S, E, node_list, name_index_dict) time_dict["Edmons-Karp"].append(time.time() - start_time) S, E, node_list, name_index_dict = deepcopy(instance) start_time = time.time() Dinic_Solve(S, E, node_list, name_index_dict) time_dict["Dinic"].append(time.time() - start_time) plot(time_dict, m_arr, "固定n为10，m与运行时间的关系", "m") def plot(time_dict, arr, title, x_label): for key in time_dict.keys(): plt.plot(arr, time_dict[key], marker=".", label=key) plt.legend() plt.xlabel(x_label) plt.ylabel("运行时间(s)") plt.title(title) plt.grid(True) plt.show() if __name__ == '__main__': # test1() test2() 5.4 结论（仅供参考）当点的数量远大于边的数量时，采用 Edmons-Karp 算法否则采用 Ford-Filkerson 算法和 Dinic 算法（在我的测试中，这两种该算法性能差不多，不过 Dinic 算法看起来更加稳健一些，当然有条件的话最好都尝试一下）

【本文地址】

公司简介

联系我们