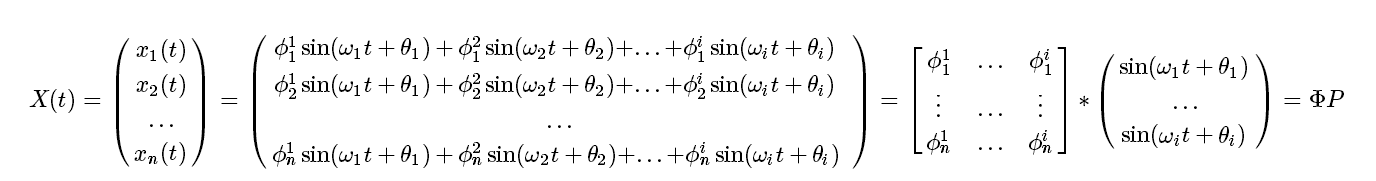什么是模态分析？什么是振型？

2023-01-23 07:09| 来源: 网络整理| 查看: 265

模态和振型是两个比较难懂的概念，涉及的理论比较多，我想通过一句话引出，然后通过逐步解释的方法去阐释这两个概念。

以一根梁为例，通过理论计算寻找其固有频率、阻尼比、振型的过程就是解析模态分析，通过实验得到的就是实验模态分析。振型其实就是坐标变换，代表了多自由度系统向单自由度系统过渡的形式。

首先认定一个前提，即多自由度系统同单自由度系统一样，在自由振动时以某一固有频率振动，不同点在于单自由度系统只有一个固有频率，而多自由系统存在多个固有频率，在这个前提下寻找一种方法，将自由振动分解为若干个简谐振动的叠加

其动力学方程为 $\LARGE \left [ M\right ]\left \{\ddot{x}(t)\right \}+\left [ K\right ]\left \{x(t)\right \}=\left \{0\right \}$ ，{ }代表向量，x''(t)和x(t)分别代表各自由度的加速度和位移向（n*1），

现在要找到一种运动，使系统的各个坐标以同一种规律运动，但幅值可以不同，也就各个坐标上的点同时达到运动行程的最大点，也同时过零点（添加动图）

先给出结论：每个自由度的时域响应是由不同振动频率的简谐运动叠加而成，例如 $\LARGE \begin{matrix}x_{1}(t)=A\sin (\omega_{1}t+\theta _{1})+B\sin (\omega_{2}t+\theta _{2})+... \\x_{2}(t)=C\sin (\omega_{1}t+\theta _{1})+D\sin (\omega_{2}t+\theta _{2})+... \\ ... \\x_{n}(t)=E\sin (\omega_{1}t+\theta _{1})+F\sin (\omega_{2}t+\theta _{2})+... \end{matrix}$

推导过程：可以假设出下式，f(t)是运动规律的时间的函数，代表了运动的形状，前面的列向量为常数向量

$\LARGE \begin{Bmatrix} x_{1}(t)\\ x_{2}(t)\\ ...\\ x_{n}(t)\end{Bmatrix}=\begin{Bmatrix} \phi _{1}\\ \phi _{2}\\ ... \\ \phi _{n}\end{Bmatrix}*f(t)$

带入到动力学方程并左乘φ T ，得到 $\LARGE \phi ^{T}M\phi \ddot{f}(t)+\phi ^{T}K\phi f(t)=0\displaystyle \displaystyle$

由理论已知（本文没讲），M正定，K正定或半正定，对上式变形得 $\LARGE \frac{-\ddot{f}(t)}{f(t)}=\frac{\phi ^{T}K\phi}{\phi ^{T}M\phi}=\lambda =\omega ^{2}$ (这里人为令λ等于ω的平方是为了后面便于计算)

对于非零列向量Φ： $\LARGE \phi ^{T}M\phi 0 ,\phi ^{T}K\phi\geq 0\Rightarrow \frac{\phi ^{T}K\phi}{\phi ^{T}M\phi}\geqslant 0$

则由 $\LARGE \ddot{f}(t)+\omega ^{2}f(t)=0\Rightarrow \left\{\begin{matrix}f(t)=asin(\omega t+\varphi) & \omega 0\\ f(t)=at+b & \omega =0 \end{matrix}\right.$

(1)对于正定系统(ω>0)

只可能出现形如 X(t) =Φ*a*sin(ωt+φ) 的同步运动,即系统在各个坐标上都是按相同频率及初相位作简谐振动

(2)对于半正定系统(ω≥0)

可能出现形如 X(t) =Φ*a*sin(ωt+φ) 的同步运动,也可能出现形如 f(t) =Φ*(a*t+b)（此时不发生弹性变形）

本文只讨论正定系统的振动情况

由以上推导已知正定系统在各个坐标上都是按相同频率及初相位做幅值不定的简谐运动

将 X(t) =Φ*a*sin(ωt+φ)中的Φ*a合写为Φ，并将X(t)代入动力学方程，化简后可得系统的特征值方程： $\LARGE （K-\omega ^{2}M）\phi=0$ $\LARGE （K-\omega ^{2}M）\phi=0$ $（K-\omega ^{2}M）\phi=0$ $\LARGE （K-\omega ^{2}M）\phi=0$ $\LARGE \begin{pmatrix} K-\omega ^{2}M \end{pmatrix}\phi=0$

根据线性代数中的克莱姆法则，由 N个方程构成的 N 元齐次线性方程组的系数行列式不为零时，齐次方程组只有零解（平凡解）。所以如果特征值方程具有非零解（非平凡解），那么系数矩阵的行列式必须为零。 $\LARGE \begin{vmatrix} K-\omega ^{2}M \end{vmatrix}=0$

到这一步就能看出，特征方程中的特征值是同步运动频率的平方，而特征向量就是振型，体现了某阶频率下，系统在各个坐标上产生的某种固定规律的运动形态

继续将行列式写为以下形式

$\LARGE \begin{vmatrix} K_{11}-\omega ^{2}M_{11}&...& K_{1n}-\omega ^{2}M_{1n}\\ ... & ... & ...\\ K_{n1}-\omega ^{2}M_{n1} & ... &K_{nn}-\omega ^{2}M_{nn} \end{vmatrix}=0$

行列式展开后得到特征多项式 $\small \omega ^{2n}+a_{1}\omega ^{2(n-1)}+a_{2}\omega ^{2(n-2)}+...+a_{n-1}\omega ^{2}+a_{n}=0$

解出n个值，并按升序排列 $\small 0 {\omega_{1}}^{2}\leqslant {\omega_{2}}^{2}\leq ...\leq{\omega_{n}}^{2}$ ，其中ωn为第n阶固有频率，ω1为基频

以上推导说明固有频率仅取决于系统本身的刚度和质量，且n自由度系统可以求出n个特征根，也就是n个固有频率

不难发现，将不同的特征根代入，解出的特征向量是不同的，特征根与特征向量一一对应，即 $\small \omega _{i}\leftrightarrow \phi ^{i}$ ， $\small \phi ^{i}=\begin{pmatrix} \phi _{1}^{i}\\ ...\\ \phi _{n}^{i}\end{pmatrix}$

证明到这一步就可以得出一个结论：一个多自由度系统在自由振动时，系统在每个坐标上的位移是由不同频率的简谐运动线性叠加而成，在某一固有频率ωi下，系统在各个坐标上都将做同一规律的运动，体现在结构整体上便是这个多自由度系统仅有一种振动形态，体现在数值上便是振型 {Φi}

将上面这段话以公式形式写出

理解了这个公式就基本上就理解了多自由度系统在自由振动时的振型叠加原理，关于这个公式有几点要做说明，公式中的 i 和 n 理应相等，但为了便于理解其中的原理我把他俩分开写，首先n代表的是系统的自由度或者坐标数，xn(t)代表多自由度系统在第n个坐标上的位移，而 i 表示在第 i 阶模态下的各个变量，比如 Φ1i 代表了第一个坐标下固有频率为 ωi 的简谐运动的幅值。

这个公式带给我们两个视角，第一：如果单独挑出这个多自由度系统的一个坐标观察，可以发现系统在这个坐标上的运动（可以理解为一个梁切成好几块，挑出其中的某一块观察其运动）是由多个频率不同的简谐运动线性组合而成。第二：对整体观察，如果把每一个自由度下同频率的分量挑出来并视为整体，那么这个多自由度系统整体可视作由 i 个频率不同的运动叠加而成，这些不同频率的运动各自的形态就是振型Φi

公式最右边的 ΦP 体现的是坐标变换的思想，即求解振型的过程就是坐标变换的过程，把物理空间变换到模态空间，振型就是模态空间的基，P就是权，为什么振型能作为基（为什么振型正交）这在后文解释，这里只是提一下这个概念，因为很多文章上来就给出一句话“模态分析就是把物理空间耦合的方程组变换到模态空间进行解耦的过程”，这句话很对，但是比较抽象，所以我觉得到了这一步可以对这句话有了进一步的理解

下面接着推导一个很关键的问题：振型到底是什么样子？

还是先给出结论：振型没有定值，它是一种系统固有特性

当 ωi 不是特征多项式的重根时，代入特征方程，由于|K-wM|=0，所以(K-wiM)Φ=0这个方程组中n个方程只有一个不独立（有一个方程不起作用，所以变成了（n-1）个方程解n个未知数），这时可以人为规定 $\small \phi ^{i}=\begin{pmatrix} \phi _{1}^{i}\\ ...\\ \phi _{n}^{i}\end{pmatrix}$ 中的一个为1，这就是归一化，归一化的方法有很多种，往往是根据实际情况进行选取，这里随便选一个为1以后，其他的都与这一个呈比例关系，所以振型可以理解是一种振幅间的比例关系，但是振幅值无法计算，在振型的推导过程中并没有别的变量牵扯进来，所以振型只与系统的M阵和K阵有关，即振型是一种固有属性

下一个问题：为什么系统要按照振型分解？（振型为什么是模态空间的基？）

由前文已知，ωi 对应Φi，ωj 对应 Φj，且均满足 $\LARGE \left\{\begin{matrix} K\phi ^{(i)}={\omega _{i}}^{2}M\phi ^{(i)}\\ K\phi ^{(j)}={\omega _{j}}^{2}M\phi ^{(j)}\end{matrix}\right. \Rightarrow \left\{\begin{matrix} \phi ^{(i)T}K\phi ^{(j)}={\omega _{i}}^{2}\phi ^{(i)T}M\phi ^{(j)}\\ \phi ^{(i)T}K\phi ^{(j)}={\omega _{j}}^{2}\phi ^{(i)T}M\phi ^{(j)}\end{matrix}\right.$

解释一下从左到右的过程，左边就是原始的特征方程在等号两边挪了一下位置，重点在于怎么变到右边，首先申明一个前提，不管是解析模态分析（本文所讲）或实验模态分析，都要满足四个假设条件

1、线性假设：结构的动态特性是线性的，也就是任何一组输入引起的输出都是各自输出的组合，其动力学特性可以用一组线性二阶微分方程来描述

2、时不变假设：结构的动态特性不随时间而变化，因而微分方程的系数是与时间无关的常数。由于不得不安装在结构上的运动传感器的附加质量，可能出现典型的时不变问题

3、可观测假设：这意味着用以确定所关心的系统动态特性所需要的全部数据都是可以观测的。为了避免出现可观测性问题，合理选择响应自由度是非常重要的

4、Maxwell互易定理：在q点输入所引起的p点的响应等于p点相同输入引起的q点的响应

正是第四条原则使得刚度矩阵和质量矩阵是对称矩阵，且对称矩阵的转置是其本身

回到原文，将左边一式等号两边分别转置后右乘 Φ(j)，得到右边一式，再对左边二式左乘Φ(i)的转置，得到右边二式，将右边两式相减得 $\LARGE \left ( {\omega_{i}}^{2}-{\omega_{j}}^{2}\right )\phi ^{(i)T}M\phi ^{(j)}=0$ ，通常第 i 阶固有频率与第 j 阶不相等， $\LARGE \Rightarrow \phi ^{(i)T}M\phi ^{(j)}=0$ ，称为振型关于质量的正交性，将其代回原式 $\LARGE \Rightarrow \phi ^{(i)T}K\phi ^{(j)}=0$ ，称为振型关于刚度的正交性，当 i=j 时, $\LARGE \phi ^{(i)T}M\phi ^{(i)}=m_{pi}$ , 称mpi为第 i 阶模态主质量， $\LARGE \phi ^{(i)T}K\phi ^{(i)}=k_{pi}$ ，称为第 i 阶模态主刚度，第 i 阶固有频率 $\LARGE \omega _{i}=\sqrt{\frac{k_{pi}}{m_{pi}}}\; \; \; \left ( i=1...n\right )$

推导到这里，就可以对振型的作用有一个大概的解释了

最初的动力学方程为 $\LARGE \left [ M\right ]\left \{\ddot{x}(t)\right \}+\left [ K\right ]\left \{x(t)\right \}=\left \{0\right \}$ ，经过前面的理论知道了X(t)=ΦP，经过替换得到

$\LARGE \Phi ^{T}[M] \Phi \ddot{P(t)}+\Phi ^{T}[K] \Phi P(t)=0 \Rightarrow \left\{\begin{matrix} m_{p1}\ddot{p_{1}(t)}+k_{p1}p_{1}(t)=0\\ \\ m_{p2}\ddot{p_{2}(t)}+k_{p2}p_{2}(t)=0\\ ...\end{matrix}\right.$

此时一个多自由度系统的方程组变成了数个单自由度方程

这样做的意义：

用语言解释一下：经过前面的推导将多自由度系统变为了数个单自由度系统，需要注意二者的所处空间完全不同，因为这两个空间的基完全不同，所以需要将物理空间的初始条件转换到模态空间，根据前文的推导，两空间坐标的变化只需左乘振型矩阵或振型矩阵的逆，所以对物理空间的初始条件向量左乘振型矩阵的逆就可得到模态空间下的初始条件向量，已知单自由度系统的时域响应公式（本文没有推导），将初始值、固有频率代入计算，得到的是模态空间的各个单自由度系统的响应，将这个模态空间的响应向量再逆变换回物理空间，得到的便是物理空间中多自由度系统在各个坐标下的响应，这个看起来复杂，其实过程跟傅里叶变化和拉普拉斯变换的道理是一样的，将时域变为频域，在频域经过简单的计算后再变回时域，由此便可简化计算

下面给出一个算例，帮助理解

一个三自由度弹簧质量系统， $\LARGE x_{0}=\begin{bmatrix} 2 & 2 & 0 \end{bmatrix}^{T }\; \; \; \; \dot{x_{0}}=\begin{bmatrix} 0 & 0 & 0 \end{bmatrix}^{T }$ ，求系统在初始条件下的响应

动力学方程为 $\large \begin{bmatrix} m & & \\ & m & \\ & & m \end{bmatrix}\begin{bmatrix} \ddot{x_{1}}\\ \ddot{x_{2}}\\ \ddot{x_{3}}\end{bmatrix}+\begin{bmatrix} 3k & -k & 0\\ -k& 2k & -k\\ 0&-k &3k \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0\end{bmatrix}$

解出固有频率 $\LARGE \omega _{1}=\sqrt{\frac{k}{m}}\; \; \; \; \; \omega _{2}=\sqrt{\frac{3k}{m}}\; \; \; \; \; \omega _{3}=2\sqrt{\frac{k}{m}}$

令Φ1i=1，解出振型矩阵 $\LARGE [\Phi] =\begin{bmatrix} 1& 1& 1\\ 2& 0& -1\\ 1& -1& 1 \end{bmatrix}\; \; \; \; \; [\Phi]^{-1}=\begin{bmatrix} \frac{1}{6} & \frac{1}{3} &\frac{1}{6} \\ \frac{1}{2}& 0 & -\frac{1}{2}\\ \frac{1}{3}& -\frac{1}{3} &\frac{1}{3} \end{bmatrix}$

解出模态空间下的初始向量 $\LARGE \left \{p_{0}\right \}=[\Phi]^{-1} \left \{x_{0}\right \}=\begin{bmatrix} 1\\ 1\\ 0\end{bmatrix} \; \; \; \; \;$ $\LARGE \left \{\dot{p_{0}}\right \}=[\Phi]^{-1} \left \{\dot{x_{0}}\right \}=\begin{bmatrix} 0\\ 0\\ 0\end{bmatrix}$

代入单自由度的时域响应公式 $\LARGE P(t)=\frac{\dot{p_{0}}}{\omega _{i}}\sin (\omega _{i}t)+p_{0}\cos (\omega _{i}t)$

最后再变换到物理空间 $\LARGE X(t)=\Phi P(t)=\begin{bmatrix} 1 & 1& 1\\ 2& 0& -1\\ 1& -1& 1 \end{bmatrix}\begin{bmatrix} \cos(\omega _{1}t)\\ cos(\omega _{2}t)\\ 0\end{bmatrix}=$ $\LARGE \begin{bmatrix} cos(\omega _{1}t)+cos(\omega _{2}t)\\ 2cos(\omega _{1}t)\\ 0\end{bmatrix}$

【本文地址】

公司简介

联系我们