| 智能优化算法(Ga,PSO,SA)高度模块化(可直接调用)python实现 | 您所在的位置:网站首页 › 人物组图简笔画 › 智能优化算法(Ga,PSO,SA)高度模块化(可直接调用)python实现 |
智能优化算法(Ga,PSO,SA)高度模块化(可直接调用)python实现
|
智能优化算法(Ga,PSO,SA)高度模块化(可直接调用)python实现
为啥做这篇文章
此篇文章基于本人数学建模实验课程的智能算法研究,老师要求用matlab实现一种优化算法分析,并且实现函数封装模块化。本人由于数模需要且比较擅长python,于是在这里记录下算法实现,方便日后比赛利用。 三大智能优化算法本质探究不要被智能蒙蔽了双眼,其实本质就是思维的转变。 我们之前的传统算法基本是遍历穷举进行可行范围内寻求目标函数的最优解。但在这里有如下几个基本思维步骤(不涉及具体实现)。 1.全局可行解随机选取 2.可行解带入目标函数求值 3.值筛选,选取当前最优值 4.当前最优值对应解进行有目标随机浮动,实现有目标随机遍历 5.2,3,4步骤进行重复。 我觉得这些步骤都看起来很简单,了解了这些基本步骤后对智能算法的原理以及实现也就更加清楚了。各种算法的差异主要体现在可行解的收敛算法。 遗传算法(ga)遗传算法有个特殊的地方,就是自变量编码问题。我们习惯性将对应维度的值转化成二进制编码然后串联组成DNA序列,然后具体计算再涉及编码解码的问题(其实本人觉得有点多此一举了)。 这里需要将可行解理解为DNA表现型。值筛选就按适应度(与目标函数有关)计算。值得关注的就是可行解的收敛算法了。 GA运用了我们大自然优胜劣汰(就是寻当前最优解),然后逐步扩大当前最优解的涉及影响范围(就是使尽量多的后代与其保持相同的DNA序列)。但这有个通病,就是容易导致可行解逐渐陷入局部最优解,而不是找到我们最需要的解(可以理解局部最优就是陷入极小值点,而全局最优是最小值点,高中数学就告诉我们这两者不一样。当然这是为了方便理解,对于离散非连续的函数可不能这么理解)。 为了解决这个问题,我们就利用变异,染色体交叉的操作来实现可行解跳出舒适圈(实现寻找其他最优解)。提高了遗传算法的感受野,更为容易寻找到目标函数的最优解。 粒子群算法(PSO)粒子群我个人觉得就可行解的收敛算法与GA不一致罢了。但我更觉得粒子群符合我们的社会行为。 粒子群随机分布,会互相联系,告知对方自己寻找到的最优解(群最优解),以及心知肚明自己碰到的最优解,这些会影响自己的加速度。然后每次迭代会改变自己的速度以及位置(高中物理就告诉我们速度是多维的,速度会改变多个维度变量的数值),最终迭代结束,找到最优解。 该算法可通过画粒子pos图(最好通过PCA将变量加权后进行降维到三维进行绘制)得出收敛的结论(现象是粒子群逐渐汇聚,但偶尔有几个跑去找其他地方的最优解了)。 模拟退火算法(SA)个人觉得退火挺有意思的。这里没有种群的概念了哈。纯物理现象。 首先温度很高,增加了自变量的感受野(也就是刚开始不会收敛),然后逐步迭代后温度降低,对非最优解的容忍度降低,逐步进入收敛过程。 本文不介绍各个算法具体原理,只是进行收敛算法的探究。 python代码实现首先给出目标函数 首先给出GA代码 import numpy as np import matplotlib.pyplot as plt def decode(x, a, b): """解码,即基因型到表现型""" xt = 0 for i in range(len(x)): xt = xt + x[i] * np.power(2, i) return a + xt * (b - a) / (np.power(2, len(x)) - 1) def decode_X(X: np.array,lb,ub,dna_num): """对整个种群的基因解码,上面的decode是对某个染色体的某个变量进行解码""" X2 = np.zeros((X.shape[0],dna_num)) for i in range(X.shape[0]): x=[] for j in range(dna_num): m=decode(X[i,10*j:10*(j+1)],lb,ub)#进行解码 x.append(m) X2[i, :] = np.array(x) return X2 def select(X, fitness): """根据轮盘赌法选择优秀个体""" fitness = 1 / fitness # fitness越小表示越优秀,被选中的概率越大,做 1/fitness 处理 fitness = fitness / fitness.sum() # 归一化 idx = np.array(list(range(X.shape[0]))) X2_idx = np.random.choice(idx, size=X.shape[0], p=fitness) # 根据概率选择 X2 = X[X2_idx, :] return X2 def crossover(X, c): """按顺序选择2个个体以概率c进行交叉操作""" for i in range(0, X.shape[0], 2): xa = X[i, :] xb = X[i + 1, :] for j in range(X.shape[1]): # 产生0-1区间的均匀分布随机数,判断是否需要进行交叉替换 if np.random.rand() f_best}, x={self.X}") sa = SA(func,-5.12,5.12,1000,30,100,0.01,0.98) sa.run() plt.plot(sa.history['T'], sa.history['f']) plt.title('SA') plt.xlabel('T') plt.ylabel('f') plt.gca().invert_xaxis() plt.show()结果如下: 1.首先我们需要注意对于变量范围的划分,我们最好首先均匀计算选点绘出离散图然后选择一个有效区间。 2.超参数一定要认真调试!我的最后一个就是超参数调不好了,靠!!! |
【本文地址】
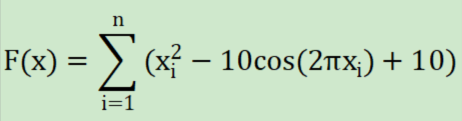 其中n=30(也就是维度)。各个变量的边界条件为[-5.12,5.12] 带入代码中。
其中n=30(也就是维度)。各个变量的边界条件为[-5.12,5.12] 带入代码中。 不知道为啥哈,SA算法不进人意,大家可自行修改超参数进行完善。我累了。
不知道为啥哈,SA算法不进人意,大家可自行修改超参数进行完善。我累了。