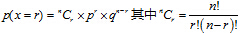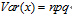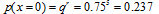【程序员眼中的统计学（6.2）】原创实现二项分布算法以及应用

作者 白宁超

2015年8月15日22:51:38

摘要：本文继统计学几何分布、二项分布、泊松分布研究的深入，基于各种分布基础概念和核心知识介绍之后。就各种分布的实现和真实环境下应用方是目的。在进行一系列相互独立实验，每次既有成功，又有失败的可能，且单次实验成功概率相等。在一系列试验中求成功的次数。这种情况下适用于本算法。本算法中在n次伯努利试验中：试验n次得到r次成功的概率、二项分布的期望、二项分布方差的具体实现。(本文原创，转载注明出处： 二项分布算法 )

统计学之离散概率分布的运用

统计学之几何分布、二项分布及泊松分布

统计学之几何分布算法

统计学之卡方分布

在进行一系列相互独立实验，每次既有成功，又有失败的可能，且单次实验成功概率相等。在一系列试验中求成功的次数。这种情况下适用于本算法。

本算法中在n次伯努利试验中：试验n次得到r次成功的概率、二项分布的期望、二项分布方差的具体实现。

在相互独立事件中，每道题答对概率为p，答错概率为q。在n个问题中答对r个问题的概率为：  这类问题称之为二项分布。表达式为：X~B(n,p)

n：表示总试验次数

X：表示n次独立试验获取成功的次数p：表示独立试验成功的概率q：表示独立试验失败的概率

假设成功概率为p，失败概率为q，n次伯努利试验中，试验次数为r的前提下满足：

1、第r次试验第一次成功：    

2、期望：

3、方差：

具体地，以书中或研究中的实际场景为例，描述算法的使用方法，包括：在该场景下算法的定义、算法中包含的符号的具体含义解释，以及具体的计算方法。

案例描述：一次竞猜游戏中共有5个问题，每一题答对的概率为0.25，假设每一次答题都是独立事件。

案例定义：答题者单次独立成功概率为0.25，失败概率为0.75，知道总共5道题目，即可求出相关答对次数。

n：表示总试验次数，n=5。

X：表示n次独立试验获取成功的次数,X=r(第r次)。p：表示独立试验成功的概率，p=0.25。q：表示独立试验失败的概率, q=1-p=0.75。

案例计算：假设成功概率为p=0.25，失败概率为q=1-p，n次伯努利试验中，总共5道题目的前提下满足：

1、答对两道题的概率：  

2、一题答不对的概率：  

4、期望：   

5、方差：

算法适用的场景及不适用的场景的描述，算法适用的数据类型描述。

优点：在试验次数一定，求成功次数时，几何分布显示不适合的情况下，给予这类问题二项分布能更好的解决。

缺点：但是面对试验次数不固定，发生事件概率的情况下，显然几何分布与二项分布都不能解决，这里也体现出泊松分布的优势。

n次试验在相同条件下进行，各个观察单位的结果独立，且只能具有相互对立的一种结果，目的：第N次试验中成功多少次。

在非独立试验情况，或者独立试验情况下获取第一次成功的概率，不适用二项分布。

本算法适用于double数据类型，默认保留两位小数，可以自行设定保留位数。

  * @param   n   int，表示总的独立事件

  * @param   r   int，表示发生r次 

  * @param   p   double，表示成功的概率

方法RSucess中：

 * @param   q    double，表示失败的概率即1-p

 * @param   ncr  double，表示成功的组合次数

* @return PX double型保留两位小数，需要n次试验r成功的概率

* @return EX double型保留两位小数，二项分布的期望

* @return VX double型保留两位小数，二项分布的方差

可行的解决方法。该部分内容一方面描述在具体的计算过程中可能导致计算结果错误或产生误差的情况，另一方面描述在程序中，什么情况下会导致何种类型的异常。

异常1：输入数据不合法，如：要求输入double数据，输入字母。

异常2：输入数据特别大，超越计算能力

误差1：计算组合结果数据保留位数，截取字符，存在一定细微误差

误差2：保留小数位数造成不精确

异常1：解决，输入不合法给予提示。

异常2：解决，进行异常捕获

误差1：解决，尽量中间计算过程不保留小数位，减小误差影响

误差2：解决，进行小数点位数自定义保留封装，根据具体精度进行设置。

该点只需给出对应的类和方法的基本描述，即给出类名，并列出具体调用的方法。

类源码：见源程序：Distributes. src. DistTools. BinoDist

本算法中在n次伯努利试验中：试验n次r次成功的概率、二项分布的期望、二项分布方差的具体实现。

见源程序：Distributes. src. DistTools. BinoDist

BinoDist.java 下包含如下方法：

RSuccess(int n,int r,double p,double q)  //试验n次独立试验，r次成功的概率

Expectation(int n,double p)               //二项分布的期望

Variance(int n,double p,double q)          //二项分布方差

调用封装方法：

NumFormat.java  下如下方法：

DecFormat(int n,double num)         //对num数值保留位数n的自行设置

factorial(int num)                   //对num数值求阶乘

类的注释如下：

方法一：第一次成功概率的方法注释以及实现

注释：

 /**  * 在n次伯努利试验中，在n次独立的伯努利试验发生r次的概率为   * P(X=r)=C_n_r*p^{r}*q^{n-r}且C_n_r=n!/(r!*(n-r)!)  * @param n int，表示总的独立事件  * @param r int，表示发生r次  * @param p double型保留一位小数，表示成功的概率  * @return PX double型保留两位小数，5道题目答对两道题的概率  */

 代码：

方法二：二项分布的期望方法注释以及实现

注释：

 /**  * 在n次伯努利试验中，二项分布的期望公式：E(X)=np   * @param n int型，表示试验的次数  * @param p double型保留一位小数，表示成功的概率  * @return EX double型保留两位小数，二项分布的期望  */

代码：

方法三：二项分布的方差方法注释以及实现

注释：

 /**  * 在n次伯努利试验中，二项分布的方差公式：Var(X)=npq  * @param n int型，表示试验的次数  * @param p double型保留一位小数，表示成功的概率  * @param q double型保留一位小数，表示失败的概率即1-p  * @return VX double型保留两位小数，二项分布的方差  */

代码：

注：PPT下载（提取码：4849）