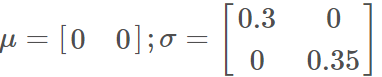| 一维(多维)高斯模型(One(Multi) | 您所在的位置:网站首页 › 二维高斯函数图像怎么画的 › 一维(多维)高斯模型(One(Multi) |
一维(多维)高斯模型(One(Multi)
|
一维高斯模型(One-dimensional Gaussian Model)
若随机变量X服从一个数学期望为 x~N( 则概率密度函数为:
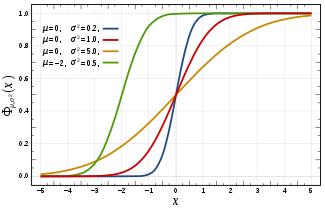
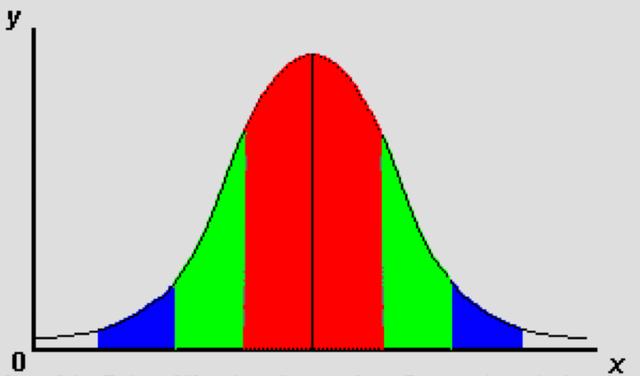
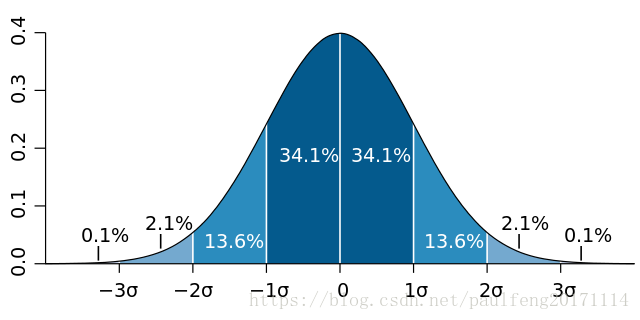
高斯分布的概率分布函数 高斯分布标准差在概率分布的数据意义 高斯分布重要量的性质 密度函数关于平均值对称平均值是它的众数(statistical mode)以及中位数(median)函数曲线下68.268949%的面积在平均值左右的一个标准差范围内95.449974%的面积在平均值左右两个标准差2σ的范围内99.730020%的面积在平均值左右三个标准差3σ的范围标准正态分布是μ=0,
注:机器学习中对于方差我们通常只除以m而非统计学中的m−1(因为均值进去一个点)。这里顺便提一下,在实际使用中,到底是选择使用1/m还是1/(m−1)其实区别很小,只要你有一个还算大的训练集,在机器学习领域大部分人更习惯使用这个版本的公式。这两个版本的公式在理论特性和数学特性上稍有不同,但是在实际使用中,他们的区别甚小,几乎可以忽略不计。 中心极限定理 正态分布有一个非常重要的性质:在特定条件下,大量统计独立的随机变量的平均值的分布趋于正态分布,这就是中心极限定理。中心极限定理的重要意义在于,根据这一定理的结论,其他概率分布可以用正态分布作为近似。中心极限定理阐明了随着有限方差的随机变量数量增长,它们的和的分布趋向正态分布。 1、参数为n和p的二项分布,在n相当大而且p接近0.5时近似于正态分布。 (有的参考书建议仅在np与n(1−p)至少为5时才能使用这一近似)。近似正态分布平均数为μ=np且方差为σ^2=np(1−p)(见下图)正态分布的概率密度函数,参数为μ = 12,σ = 3,趋近于n = 48、p = 1/4的二项分布的概率质量函数。 2、一泊松分布带有参数λ当取样样本数很大时将近似正态分布λ. 近似正态分布平均数为μ=λ且方差为σ^2=λ.,这些近似值是否完全充分正确取决于使用者的使用需求。 其他一些相关分布介绍
多维单高斯是如何由一维单高斯发展而来的呢? 同理,高维情形相同!
再比如:
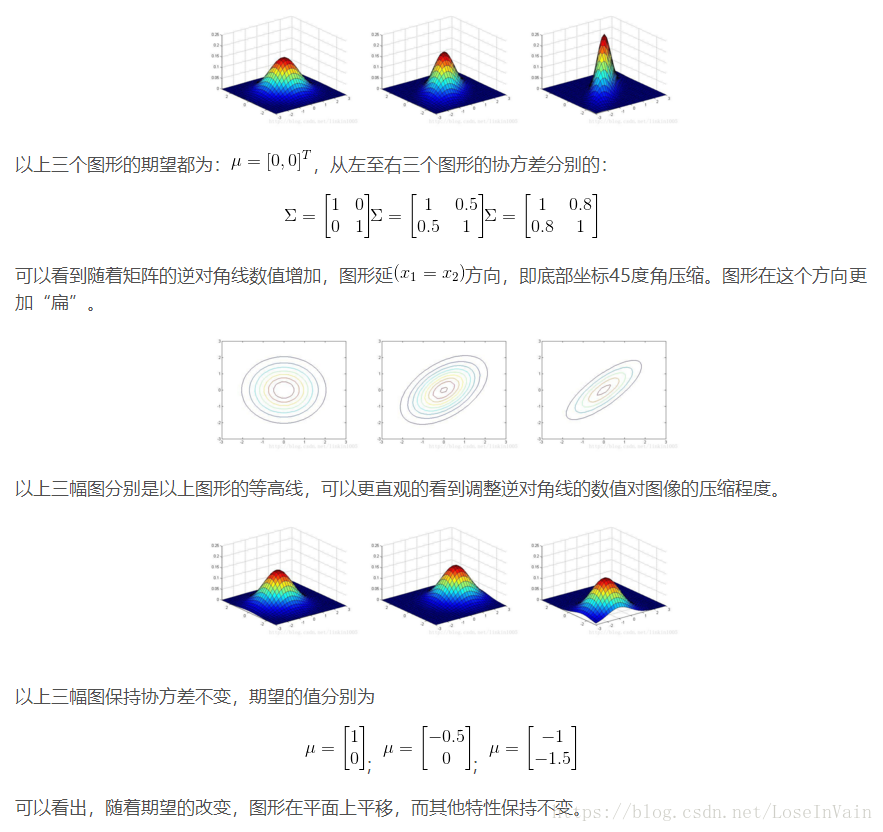
以下是几种高斯模型: 上面几个图很好理解,只是在改变协方差矩阵对角线上的数改的越大,图形就越尖! 这上面几个图其实就是高斯模型在平面上的投影,等高线上的(x,y)概率是相等的。 1. 针对二维高斯分布,若随机变量中的两个维度不相关,协方差矩阵对对角阵,则如下图所示 构成一个圆形。 2.若两个维度数据相关,协方差矩阵为对称矩阵,则如下图所示 构成一个椭圆形 3.针对二维高斯分布,协方差矩阵的对角线元素为 能够看出,图形的形状跟方向跟协方差矩阵 统计学习的模型有两种,一种是概率模型,一种是非概率模型。 所谓概率模型,是指训练模型的形式是P(Y|X)。输入是X,输出是Y,训练后模型得到的输出不是一个具体的值,而是一系列的概率值(对应于分类问题来说,就是输入X对应于各个不同Y(类)的概率),然后我们选取概率最大的那个类作为判决对象(软分类–soft assignment)。所谓非概率模型,是指训练模型是一个决策函数Y=f(X),输入数据X是多少就可以投影得到唯一的Y,即判决结果(硬分类–hard assignment)。 所谓混合高斯模型(GMM)就是指对样本的概率密度分布进行估计,而估计采用的模型(训练模型)是几个高斯模型的加权和(具体是几个要在模型训练前建立好)。每个高斯模型就代表了一个类(一个Cluster)。对样本中的数据分别在几个高斯模型上投影,就会分别得到在各个类上的概率。然后我们可以选取概率最大的类所为判决结果。 从中心极限定理的角度上看,把混合模型假设为高斯的是比较合理的,当然,也可以根据实际数据定义成任何分布的Mixture Model,不过定义为高斯的在计算上有一些方便之处,另外,理论上可以通过增加Model的个数,用GMM近似任何概率分布。 混合高斯模型的定义为: 其中K为模型的个数; 如下是李航老师《统计学习方法》中给出的GMM定义:
附上一个大佬写的GSM,深入浅出值得一看漫谈 Clustering (3): Gaussian Mixture Model |
【本文地址】
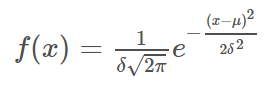 高斯分布的期望值
高斯分布的期望值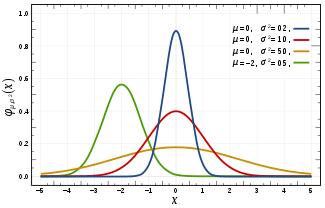
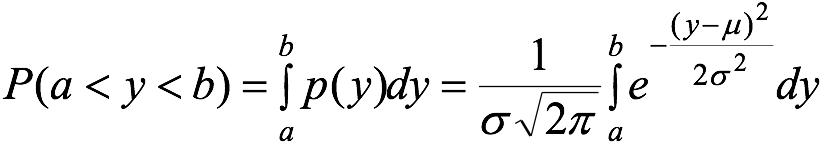
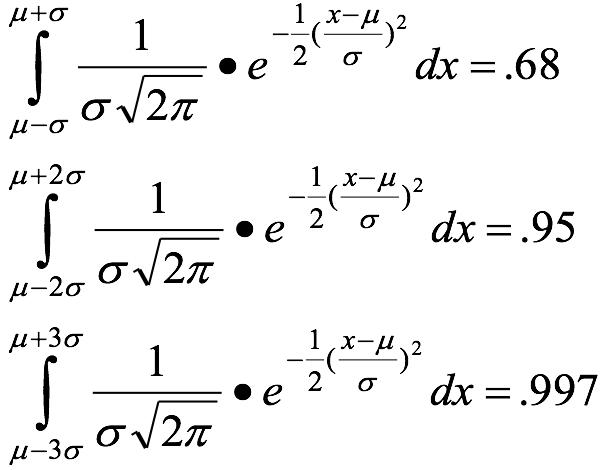
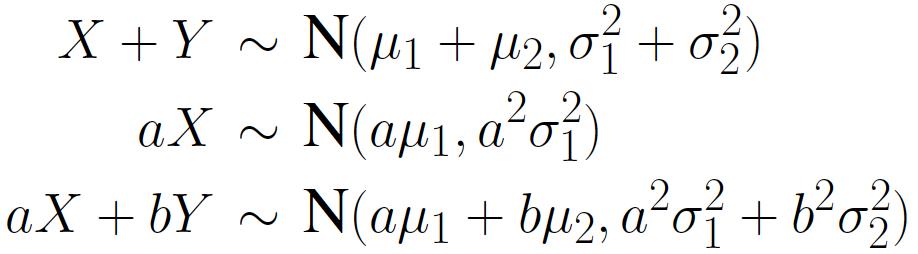





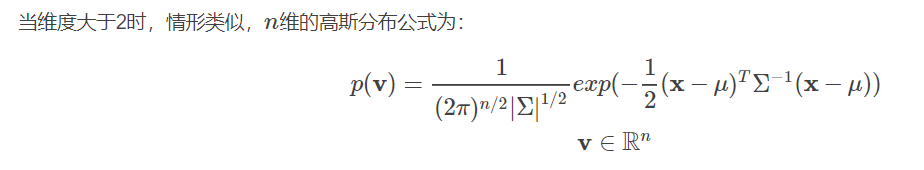 举个栗子:
举个栗子: