| 向量的线性相关、矩阵的秩总结 | 您所在的位置：网站首页 › 为什么正交向量组必线性无关 › 向量的线性相关、矩阵的秩总结 |
向量的线性相关、矩阵的秩总结
|
一些杂谈（可以不看）
这次尝试使用了MD记笔记。我这人真的挺奇怪，对着电脑记笔记比对着纸笔更专注。。。希望期末线代高数大物不会抛弃我。。。 以下是正文： 本文综合了网络各处的大佬的想法，综合总结成了笔记，仅作个人学习用。如我的行为如果有冒犯到您，请联系我，我将立即修改或删除。 前置概念 向量组和向量组的线性表示如果向量组\(B:\beta_1,\beta_2...\beta_q\)中的每个向量都可由向量组\(A:\alpha_1,\alpha_2...\alpha_n\)线性表示，则称向量组B可由向量组A线性表示。（也称为两个向量组等价） 假设\(B\)由\(A\)表示： $\left\{\begin{matrix} \beta = c_{11}\alpha_1+c_{21}\alpha_2+\cdots+c_{p1}\alpha_p\\ \beta = c_{12}\alpha_1+c_{22}\alpha_2+\cdots+c_{p2}\alpha_p\\ \cdots \\ \beta = c_{13}\alpha_1+c_{23}\alpha_2+\cdots+c_{p3}\alpha_p \end{matrix}\right.$观察可知：一个向量组表示另一向量组就是矩阵乘法的关系。因此我们改写为矩阵形式： $\begin{bmatrix}\beta_1 ,\beta_2, \cdots ,\beta_3 \end{bmatrix}= \begin{bmatrix}\alpha_1 ,\alpha_2, \cdots ,\alpha_3 \end{bmatrix} \begin{bmatrix} c_{11} & c_{12} & \cdots &c_{1q} \\ c_{21} & c_{22} & \cdots &c_{2q} \\ \vdots & \vdots & &\vdots \\ c_{p1} & c_{p2} & \cdots &c_{pq} \end{bmatrix}_{p\times q}$即：\(B=A\times C\)系数矩阵。 性质若向量组\(\alpha_1,\alpha_2,\cdots,\alpha_s\)可被向量组\(\beta_1,\beta_2,\cdots,\beta_t\)线性表示，则： $R(\alpha_1,\alpha_2,\cdots,\alpha_s)\le R(\beta_1,\beta_2,\cdots,\beta_t)$这里需要用到秩的概念，建议看完下面再来这里。 线性相关 定义如果一组向量中至少有一个是多余的，没有对张成空间作出任何贡献，你有多个向量，并且可以移除其中一个而不减少张成的空间，称线性相关。 对于一个二维空间，只需要任意两个不共线的非零向量即可张成整个空间。此时称这两个向量线性无关； 假如此刻再次加入任意一个属于该空间的向量，这个新的向量对构成此空间没有任何作用（删掉它不影响空间的形成），则现在称这三个向量线性相关。此向量便是冗余的。 线性无关也可理解为：在张成的最大空间上，每个维度有且只有一个支撑向量的向量组。 另一种定义（百度百科、书本）在向量空间V的一组向量\(a_1,a_2...a_m\)，如果存在不全为零的数\(k_1, k_2,...,k_m\)，使： $k_1a_1+k_2a_2+...+k_ma_m=0$ 那么称向量组A是线性相关的。这个概念不够直观，但是 可以用来计算、判断。 极大无关组（极大线性无关向量组）记得前文提到的一组有冗余向量的向量组吗？在这一组向量组中取一部分的向量，让这一部分向量不仅线性无关，并且不能再加入更多向量继续保持线性无关，那么这一组向量就是原向量组的极大无关组。因此：向量组与它的极大无关组等价。 也就是说，当我们删除一个向量组的所有冗余向量后，剩下的就是原向量组的极大无关组。 极大无关组可能不唯一，但其包含的向量数一定唯一。 线性组合\(n\)个向量\(\alpha\)（的倍数）相加形成新的向量\(\beta\)： $\beta = \sum_{i=1}^{n}k_i\alpha_i$则称向量\(\beta\)是向量组\(\alpha_i\)的一个线性组合，向量\(\beta\)可由向量组\(\alpha_i\)的线性表示。 理解线性相关和线性表示的关系一组线性相关的向量组，其中必定有向量是其他向量的线性组合。 若最大空间的子空间拥有冗余向量（可以找到线性组合），则向量组线性相关。 正交向量组正交：垂直； 两两正交的向量组被称为正交向量组； 若都为单位向量，则被称为规范正交向量组。 Schmidt正交化updating 线性相关的简单性质正交向量组线性无关； 含零向量的向量组线性相关； 向量组线性相关 \(\Leftrightarrow\) 向量组中至少有一个向量是冗余的 \(\Rightarrow\) \(n+1\) 个 \(n\)维向量总是线性相关。个数大于维数必相关 不太直观的性质如果向量组\([a_1,a_2,a_3...a_n]\)线性无关，向量组\([a_1,a_2,a_3...a_n,b]\)线性相关，那么： 向量\(b\)可由向量组\([a_1,a_2,a_3...a_n]\)线性表示，且表达式的系数唯一确定。 证明？不想看书了，教材写得好差，有时间再补上吧。。。 线性无关向量组的加长向量组仍然线性无关。 //但是什么是加长向量组？// 假如二维向量\(a(x,y)\)增加了一个分量（维度），变成了\(a(x,y,z)\)，这个向量就加长了。假如向量组里的每一个向量都加长了，就形成了加长向量组。 可以想象平面内的两个向量同时向第三维增加一个分量的情况。两个向量虽然在三维空间里面形成了一个新的平面，但仍未升维，两个向量不可能凭空多出一个维度，也不会因为到了新的平面而平白无故共线。 狗嘴里吐不出象牙。 矩阵的秩 通俗理解矩阵的秩，代表了某个方程组（向量组）的有效方程个数。 在对方程组（系数矩阵）进行化简（阶梯矩阵）之后，会发现有的矩阵表面看上去“满满当当”，实际上有好多没有起到作用的\(0\)行！！ 比如对于矩阵\(A\)： $\begin{bmatrix}1&1&2&3\\1&-1&4&1\\1&2&1&4\\1&1&2&3\end{bmatrix}\Rightarrow \begin{bmatrix}1&0&3&2\\0&1&-1&1\\0&0&0&0\\0&0&0&0\end{bmatrix}$虽然是\(4\)阶方阵，但化简之后非\(0\)行只有\(2\)行，因此其秩为\(2\)。 $R(A)=2$前面的极大无关向量组吗？它包含的向量个数就是这个向量组的秩。 相关概念如果一个方阵的秩等于其行数，那么称这种矩阵为满秩矩阵，否则称为降秩矩阵。 因为一个可逆矩阵的行列式一定不为0，而矩阵的秩为非零子式的最高阶数，所以可逆矩阵一定是满秩矩阵。 假设一个秩不满的矩阵，对于它最大的满秩子方阵，我们称这个子方阵为最高阶非0子式。所以上面提到的矩阵\(A\)的最高阶非0子式为： $\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}$从线性变换的角度来说，矩阵是对于整个空间的变换。而这个矩阵的秩代表了变换后的空间的维度。 因此，一个矩阵的逆矩阵表示了将扭曲后的空间变回原来样子的操作。 只有在同维度下，可逆才有意义。若空间被降维，信息会丢失，那么就不再能变回以前的空间了。（此处可想像3B1B视频里面二维空间被压缩到一维的动画） 我想再去复习一下3B1B的这个视频 列空间、行空间复习这里复习此概念是为了更好地理解矩阵的秩的部分性质。 一般矩阵乘法计算方法： $\begin{bmatrix}1 &4 \\2 &5 \\3 &6\end{bmatrix} \begin{bmatrix}x_1 \\x_2 \end{bmatrix} =\begin{bmatrix} 1x_1+4x_2 \\ 2x_1+5x_2 \\ 3x_1+6x_2 \end{bmatrix}$这种以行为主的内积运算适合电脑计算，但是不利于理解。 因此我们引入一个更高维度的视角——列向量： $\begin{bmatrix} {\color{Orange} 1}&{\color{Purple} 4}\\{\color{Orange} 2}&{\color{Purple} 5}\\{\color{Orange} 3}&{\color{Purple} 6}\end{bmatrix} \begin{bmatrix}x_1 \\x_2 \end{bmatrix} =x_1\begin{bmatrix} {\color{Orange} 1}\\{\color{Orange} 2}\\{\color{Orange} 3}\end{bmatrix}+ x_2\begin{bmatrix} {\color{Purple} 4}\\{\color{Purple} 5}\\{\color{Purple} 6}\end{bmatrix}$
而在 \(x_1\begin{bmatrix} {\color{Orange} 1}\\{\color{Orange} 2}\\{\color{Orange} 3}\end{bmatrix}+ x_2\begin{bmatrix} {\color{Purple} 4}\\{\color{Purple} 5}\\{\color{Purple} 6}\end{bmatrix}\) 中，任意的\(x_1,x_2\)可以与这两个向量组合，张成一个空间。这个空间被称为这两个列向量所张成（Span）的列空间（Column Space）。 因此对应地，我们也有行空间 (Roll Space)存在：
\(0\le R_{(A_{m\times n})}\le \min(m,n)\) \(R_{(A^T)}=R_{(A)}\) \(R\begin{bmatrix}A&0\\0&B\end{bmatrix}=R\begin{bmatrix}0&A\\B&0\end{bmatrix}=R_{(A)}+R_{(B)}\) \(R\begin{bmatrix}A&0\\C&B\end{bmatrix}\ge R_{(A)}+R_{(B)}\) 矩阵乘以可逆矩阵，秩不变。如：\(R_{(B^{-1}AB)}=R_{(A)}\) \(R_{(A\pm B)}=R_{(A)}+R_{(B)}\) 重要性质！（西尔维斯特不等式） 若\(A\)为\(m\times n\)矩阵,\(B\)为\(n\times l\)矩阵（\(A,B\)矩阵可以相乘），则：\(R_{(A)}+R_{(B)}-n\le R_{(AB)}\le \min(R_{(A)},R_{(B)})\) 证明：（证明过程较重要） 设置一个矩阵\(\begin{bmatrix}A&0\\E_n&B\end{bmatrix}\)； 可以知道经过初等变换，这个矩阵可以把左上角和右下角变为0： \(\begin{bmatrix}E_m&-A\\0&E_n\end{bmatrix}\begin{bmatrix}A&0\\E_n&B\end{bmatrix}\begin{bmatrix}E_n&-B\\0&E_l\end{bmatrix} =\begin{bmatrix}0&-AB\\E_n&0\end{bmatrix}\) to be updated... |
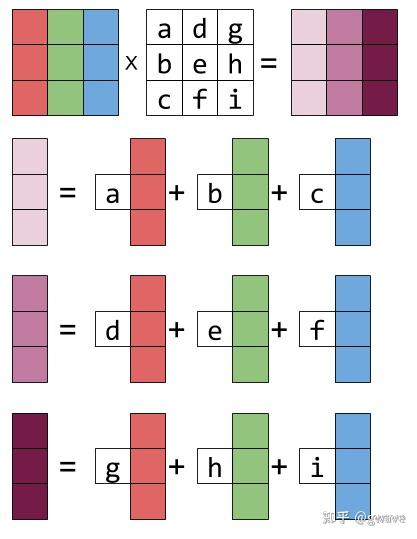来源知乎 矩阵乘法核心思想（1）：列空间
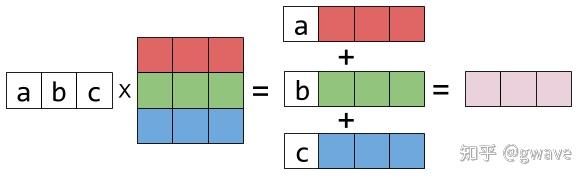来源知乎 矩阵乘法核心思想（2）：行空间【本文地址】