关于混沌，氢弹之父乌拉姆做了什么？

原创 丁玖 返朴

在确定意义下“混沌”定义问世之前，乌拉姆对其早期的探索——现代遍历理论——进行了深入研究，提出了影响深远的问题、给出了算法，并猜测了收敛性，开启了计算遍历理论的新领域。在约克及合作者关于“存在性”数学论证的基础上，华裔数学家李天岩独立给出了计算不变密度函数的数值方法并证明了收敛性，亦是计算遍历理论先驱。

撰文 | 丁玖（美国南密西西比大学数学系教授）

伟大的人物通常也是幽默家。氢弹之父乌拉姆（Stanislaw Ulam，1909-1984）曾有一句诙谐之语：“把混沌研究称为‘非线性分析’，就好比把动物学说成是‘非大象一类动物的研究’。”

事实上，虽然确定性意义下的“混沌”定义迟至上世纪70年代中期才问世，然而，对它“遍历性”的探索比之更早四十五年就开始了：以30年代初的冯·诺伊曼平均遍历定理和伯克霍夫逐点遍历定理这两个经典遍历定理为主要代表，而现代遍历理论的研究可以说是以乌拉姆为领头羊的。

探索“混沌”的“不变密度函数”法

从我之前的文中可知，要想发现混沌映射S迭代点轨道的统计分布，就必须找到对应的弗罗贝尼乌斯-佩隆算子PS的密度函数不动点，即求出不动点方程PS f = f的密度函数解，称为不变密度函数。它定义了一个绝对连续的概率测度，称为该映射的不变测度，其“不变性”意指任一子区间的测度值等于它在S下的逆像的测度值。只要映射关于该不变测度是遍历的，根据伯克霍夫逐点遍历定理，我们就能通过这个不变测度来描绘出混沌轨道的统计性质。称概率测度μ是绝对连续的，意思是指μ可由积分表示，即存在一个密度函数f，使得所有子区间I的测度值μ(I) 等于积分 ∫I f(x) dx。与绝对连续的测度相对立的是奇异的测度，如著名的狄拉克测度。

伯克霍夫逐点遍历定理可简述为：若具有不变测度μ的映射S是遍历的，则对μ而言几乎所有的初始点x0，时间平均 = 空间平均，即

。

“遍历”一词在数学上是何意思呢？我先用一例来说明“不遍历”的含义，帮助想象“遍历”意味着什么。定义一个将[0, 1]映到自身的映射S：当0 ≤ x < 1/4时，S(x) = 2x；当1/4 ≤ x < 3/4时，S(x) = 2x – 1/2；当3/4 ≤ x ≤ 1时，S(x) = 2x – 1。下面是S的图象：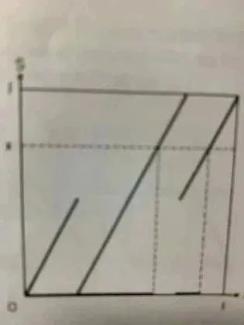

易知在S下，区间[0, 1/2]的逆像是[0, 1/2]，区间[1/2, 1]的逆像是[1/2, 1]，即S-1([0, 1/2]) = [0, 1/2])和S-1([1/2, 1]) = [1/2, 1])。这表示[0, 1]的子区间[0, 1/2]和[1/2, 1]是S的不变集。由于这两个不变集的存在，原先的映射S实际上可以分解成两个互不相干的映射S1: [0, 1/2] → [0, 1/2]和S2: [1/2, 1] → [1/2, 1]，它们分别是S在子区间[0, 1/2]和[1/2, 1]上的限制，其各自的图象分别是上面S图象的左下半个和右上半个。尽管长度（实变函数论中勒贝格测度的通俗说法）是S的不变测度，但是伯克霍夫逐点遍历定理此时并不成立，例如当初始点x0属于[0, 1/2]时，由于所有迭代点都在[0, 1/2]内，[0, 1/2]的时间平均为1；若x0属于(1/2, 1]，由于所有迭代点都不在[0, 1/2]内，它的时间平均为0。而[0, 1/2]的空间平均却为区间长度1/2，因此对于这个例子，时间平均并不等于空间平均。

从上面这个非遍历的映射例子可以想出“遍历映射”的定义。对于任意一个将定义域映到自身的映射，总有两个平凡的“不变集”，它们是空集和定义域本身，因为它们在该映射下的逆像就等于自己。如果映射本质上不存在“非平凡”的不变集，即不存在定义域的一个非平凡子集，使得它与其在映射下的逆像是同一个集合，则它是遍历的。简言之，如果映射仅有平凡不变集，它就是遍历的。

何时存在“不变密度函数”？

一个自然的问题就出现了：给定映射S: [0, 1] → [0, 1]，它所对应的弗罗贝尼乌斯-佩隆算子PS有不变密度函数吗？先回忆该算子的定义：对每一个[0, 1]上的可积函数f，

我在《》中用简单易懂的例子引进了这个算子。

考虑“减半映射” S(x) = x/2，它的定义域是[0, 1]，值域是[0, 1/2]。易知当0 ≤ x ≤ 1/2时，S-1([0, x]) = [0, 2x]；当1/2 < x ≤ 1时，S-1([0, x]) = [0, 1]。因此PSf的表达式为：当0 ≤ x ≤ 1/2时，PSf(x) = 2f(2x)；当1/2 < x ≤ 1时，PSf(x) = 0。由此显见，不动点函数方程PSf(x) ≡ f(x)只有零解f(x) ≡ 0。这并不奇怪，因为所有迭代点数列{Sn(x0)}都收敛到S的唯一不动点0，故无绝对连续的不变测度。顺便说一下，对减半映射，非绝对连续的在0点处的狄拉克测度是其不变测度。

上面的例子比较简单，容易理解，下面是一个非线性映射的例子，它也同样没有绝对连续的不变测度，即它所对应的弗罗贝尼乌斯-佩隆算子没有非零不动点。这个映射定义如下：当0 ≤ x ≤ 1/2时，S(x) = x/(1 - x)；当1/2 < x ≤ 1时，S(x) = 2x – 1。这时，懂得初等微积分并精通高中代数的读者容易算出PSf的表达式为

PSf(x) = (1+x)-2f(x/(1+x)) + (1/2)f(1/2+x/2)。

在洛速达（Andrzej Lasota，1932-2006）与麦基（Michael Mackey，1942-）合著的书Chaos, Fractals, and Noise：Stochastic Aspects of Dynamics（《混沌、分形与噪音：动力学的随机方面》）第六章第二节内，作者给出了上述算子只有零函数这个唯一不动点的证明。

注意到前面两个例子的不同之处：第一个映射的导数恒等于1/2，它严格小于1；但第二个映射的导数在(0, 1]上处处严格大于1，但在x = 0处等于1。这向我们提出一个问题：如果一个映射在定义域区间上导数除了几个例外点外处处存在，并且导数的绝对值都严格大于1，其对应的弗罗贝尼乌斯-佩隆算子一定有非零不动点吗？满足上述导数条件的映射被称为是“逐段拉长的”，这个性质是混沌的一个发源地，但不是必要条件，因为混沌的逻辑斯蒂映射S4(x) = 4x(1-x)并非是逐段拉长的。纵观混沌观念发展史，乌拉姆无疑属于最早几个对此性质进行过探索的数学家之一。

学过初等微积分的读者应该知晓，逐段拉长的映射不可能在整个定义域区间上处处可微，否则根据被称为“微分学基本定理”的拉格朗日中值定理，该映射的值域区间将比定义域区间更长，这与值域包含于定义域的基本假设相矛盾。我们熟悉的逐段拉长的帐篷映射T在x = 1/2这一点导数不存在这一事实也表明了这点。因此，逐段拉长的区间映射只能通过“分段可微”而实现“逐段拉长”。

乌拉姆传奇

乌拉姆是“非线性分析”这门综合性研究领域的先驱，实际上他与终生朋友冯·诺伊曼（John von Neumann，1903-1957）及物理学家费米（Enrico Fermi，1901-1954）等几位智者在从事原子弹研制中创建了这门学科。多年前，我读过乌拉姆文集Science, Computers, and People（《科学、计算机及故友》）。数学科普家伽德纳（Martin Gardner, 1914-2010）撰写的前言第一段是：“乌拉姆， 或如同他朋友所称之的斯坦，是那些伟大的创造型数学家之一，这些人不仅对数学的所有领域感兴趣，而且同样对物理及生物科学亦然。和他好朋友冯·诺伊曼一样而与他众多的同行不一样的是，乌拉姆不可被分类为纯粹或应用数学家。在那些与应用问题没有一丝一毫关联的纯粹地带，以及在数学的应用中，他都从不停止寻找同样多的美和激动。”

乌拉姆是犹太人，他的出生地利沃夫原属奥匈帝国下的波兰，现属乌克兰，位于国土的西部，所以他是波兰/乌克兰裔数学家，在“万神殿”网页（pantheon.world）上被列为有史以来最传奇的十位乌克兰数学家之首。在他那本我已读过三遍的脍炙人口的自传Adventures of a Mathematician（《一位数学家的经历》）一开头，乌拉姆就告诉读者，他四岁时就对家中客厅铺的波斯地毯上的几何图案着迷。当他身为律师的父亲对此不以为然而笑起来时，他心里自言自语道：“他笑是因为他认为我是幼稚的，但是我知道这些是令人好奇的模式。我知道我父亲所不知道的某样事情。” 这或许就是他终生热爱探讨新事物的天赋之才的最初显示。他喜欢提出问题以及解决问题的另一个佐证是，在上世纪30年代波兰数学学派名扬天下之时，以泛函分析集大成者巴拿赫（Stefan Banach，1892-1945）为首的波兰数学精英在苏格兰咖啡馆讨论数学及时记下的数学问题录——现在国际数学界名闻遐迩的《苏格兰书》——以二十多岁时的乌拉姆贡献的问题最多！

正是由于喜欢与人讨论，喜欢提出问题，乌拉姆从他大脑里萌芽而出的“对要点的感觉”，日后成了几个数学领域的开始之旅。比如，“细胞自动机理论”最初是他向冯·诺伊曼提出来的；“蒙特卡罗法”的思想来自于他对数论和积分棘手问题的思考；后来掀起孤立子和混沌研究热潮的“非线性分析”，是从他玩弄计算机键盘的手指中开始汩汩流出的。与