三维空间曲线曲率半径计算

2024-07-08 18:41| 来源: 网络整理| 查看: 265

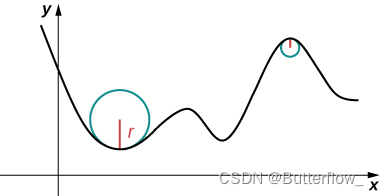
曲率

曲率的概念提供了一种测量平滑曲线转动程度的方法。圆具有恒定的曲率，圆的半径越小，曲率越大。曲线的曲率半径所对应的圆，即在该点具有与曲线相同的二阶导数对应的圆。

定义

设 C 为平面或空间中的光滑曲线，由下式给出 $\mathbf{r}(s)$ ，s 是弧长参数。在 s 点的曲率 $\kappa$ 是

$\kappa=\left\|\frac{d\operatorname{T}}{ds}\right\|=\left\|\mathbf{T}^{\prime}\left(s\right)\right\|.$

曲率定义中的公式在计算方面不是很有用。特别地，回想一下 $\mathbf{T}\left(t\right)$ 表示给定向量值函数 $\mathbf{r}\left(t\right)$ 的单位切向量， $\mathbf{T}\left(t\right)$ 的公式是 $\mathbf{T}\left(t\right)=\frac{\mathbf{r}^{\prime}(t)}{\left\|\mathbf{r}^{\prime}(t)\right\|}$ 。首先需要用弧长参数 s 来表示 $\mathbf{r}\left(t\right)$ ，然后求函数 $\mathbf{r}\left(s\right)$ 的单位切向量 $\mathbf{T}\left(s\right)$ ，然后求 $\mathbf{T}\left(s\right)$ 对 s 的导数。这是一个繁琐的过程。幸运的是，曲率有等价的公式。

曲率的向量公式

如果 C 是由 $\mathbf{r}\left(t\right)$ 给出的光滑曲线，则 C 的曲率 $\kappa$ 为

$\kappa=\frac{\left\|\mathbf{T}^{\prime}\left(t\right)\right\|}{\left\|\mathbf{r}^{\prime}\left(t\right)\right\|}.$

如果 C 是一个三维曲线，那么曲率可以由公式给出

$\kappa=\frac{\left\|\mathbf{r}^{\prime}\left(t\right)\times\mathbf{r}^{\prime\prime}\left(t\right)\right\|}{\left\|\mathbf{r}^{\prime}\left(t\right)\right\|^3}.$

【本文地址】

公司简介

联系我们