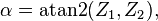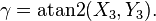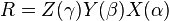| 欧拉角(Euler angles) | 您所在的位置:网站首页 › x的取值范围怎么看图解 › 欧拉角(Euler angles) |
欧拉角(Euler angles)
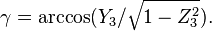
有趣的是反consine函数都可以获得两个可能的值,从几何的角度来看,只有一个答案才是合法的 当欧拉角被定义成一系列的旋转,所有的答案都可能是合法的,但是但是只有一个是符合旋转顺序的。这是因为如果旋转顺序不事先确定的话,得到结果参考系 的旋转序列并不是唯一的。
为了计算,使用atan2(y,x)去表示角可能会更有用。
泰特-布莱恩角
Tait–Bryan angles. z-y′-x″ sequence (intrinsic rotations; N coincides withy’) (Tail-Bryan角。z-y'-x''顺序, 序列(内旋; N 与 y’重合)) 欧拉角的第二种表达形式被叫做Tail-Bryan角,在通过Peter Guthrie Tail和Gerge H. Bryan努力之后,Tail-Bryan角的定义和表示与经典欧拉角的表示方法类似。 唯一的不同是 Tail-Bryan角 使用三个轴上的旋转角度去表示。(例如 x-y-z或者x-y'-z''),然而经典欧拉角的第一个旋转角度和第三个旋转角度都是围绕同一个轴的 例如(z-x-z,或者 z-x'-z'')。
这会产生一个不同于经典欧拉角中的交轨线。在经典欧拉角中,这个交轨线是两个相对应的笛卡尔平面的交线,(当欧拉角为0时,平行的两个笛卡尔平面,例如xy和XY平面)。 在第二种情况中Tait-Bryan角中,它是两个不对应的平面的交线(当欧拉角为0时,互相垂直的两个平面,例如:xy和YZ平面)。 约定
基本旋转既可以围绕着原始未移动的坐标系进行(外旋),也可以围绕那些已经经过几次基本旋转的正在旋转的坐标系的轴进行(内旋)。 有6种旋转的顺序可供选择,分别是: x-y’-z″ (内旋) or x-y-z (外旋)y-z’-x″ (内旋) or y-z-x (外旋)z-x’-y″ (内旋) or z-x-y (外旋)x-z’-y″ (内旋) or x-z-y (外旋)z-y’-x″ (内旋) or z-y-x (外旋): 此序列的内旋被叫做: 偏航(绕z旋转), 俯仰(绕y'旋转) 和 翻滚(绕x''旋转) y-x’-z″ (内旋) or y-x-z (外旋) 可供选择的命名 泰特-布莱恩角中 z-y'-x''这个序列(内旋) 通常被叫做航海角,因为他们可以用来描述一艘船或者一架飞行棋的方向,或者可以叫做万向角,也可以把这几个 旋转叫做 heading(摆头),elevation(俯仰)和bank(倾斜),或者叫做 yaw(偏航),pith(俯仰)和roll(翻滚)。注意第二套叫法也被用在三个飞行器轴中
内旋是发生在正在旋转的坐标系中的坐标轴上的旋转 XYZ坐标系旋转,xyz坐标系静止不动,三个内旋可以使XYZ坐标系指向任何一个方向。欧拉角或者泰勒-布莱恩角中(α, β, γ)是这三个旋转的幅度 例如目标方向可以这样抵达: XYZ 绕Z轴(初始时与z轴重合的那个轴)旋转角度α. 现在X 轴位于交轨线上.XYZ绕现在的X轴角度为β. Z轴现在已经位于其最终的位置, X轴还停留在交轨线上.XYZ绕新的Z轴角度为γ 上面提到的变量让我们可以总结出:三个基本旋转分别是绕着z,x',z''进行的。实际上这组旋转经常被叫做z-x'-z''序列。欧拉角和泰勒-布莱恩角中变量命名 一般都是这样的。有时这样的旋转序列也被叫做z-x-z,Z-X-Z,或者是3-1-3,但是这样命名容易与外旋产生分歧,所以有必要 指出是内旋还是外旋。
 Any target orientation can be reached, starting from a known reference orientation, using a specific sequence of intrinsic rotations, whose magnitudes are the Euler angles of the target orientation. This example uses the
z-x′-z″sequence.
Any target orientation can be reached, starting from a known reference orientation, using a specific sequence of intrinsic rotations, whose magnitudes are the Euler angles of the target orientation. This example uses the
z-x′-z″sequence.
可以用旋转矩阵表达内旋,例如
如果使用左乘列向量表达这个旋转组合,结果是
用右乘横向量的表达式和这个是一样的。
外旋 外旋是用围绕固定坐标系xyz的坐标轴的旋转角度进行标识的。 xyz是固定不懂的,而XYZ旋转, 开始时XYZ和xyz是重合的,经过三个绕xyz轴的基本旋转 XYZ可以达到指定的方向。同样 欧拉角或泰勒-布莱恩角中的三个基本旋转的角度也用(α, β, γ进行表示 例如,最终旋转可以用下面的步骤进行表示: XYZ坐标系绕z轴α. 现在X轴与x轴的角度为α.XYZ坐标系再绕x轴β. 现在Z轴与z轴的角度为β.XYZ第三次绕z轴旋转γ. 总的来说,上面过程中,这三个基本旋转是围绕z,x,z轴进行的。实际上 这个也经常被定义为z-x-z或者3-1-3,在欧拉角和泰勒-布莱恩角中都是这样命名的  一个用欧拉角表示的旋转 (α,β, γ) = (−60°, 30°, 45°), z-x’-z″序列 内旋
一个用欧拉角表示的旋转 (α,β, γ) = (−60°, 30°, 45°), z-x’-z″序列 内旋
 一个和上图相同的旋转 (γ, β, α) = (45°, 30°, −60°), z-x-z序列 外旋
一个和上图相同的旋转 (γ, β, α) = (45°, 30°, −60°), z-x-z序列 外旋
Any extrinsic rotation is equivalent to 用旋转矩阵可以表达外旋序列,例如
用左乘竖向量的方式可以表达为
右乘横向量的表达式与这个是一致的
万象移动关系  Euler basic motions of the Earth. Intrinsic (green), Precession (blue) and Nutation (red)
Euler basic motions of the Earth. Intrinsic (green), Precession (blue) and Nutation (red)
欧拉基本移动是通过改变欧拉角中其中一个角,同时保持另外两个角不变而得到的。 欧拉旋转从来不会基于外部参考系,或基于相对旋转的参考系的旋转表示。 但是在某些混合使用的情况下,它们会组成一个混合轴的旋转系统。 如左图,第一个旋转角度使交轨线绕着外部的z轴进行旋转,第二个旋转角度是围着交轨线进行旋转的,第三个旋转角度是个围绕着在体内固定轴移动的内旋。(为何第三个被称为内旋?这里理解有误?) 这些旋转被称作 旋进 点头和内旋(自旋)。举个例子,一个陀螺,这个陀螺绕着自己的对称轴进行旋转,这个对应于他的内旋,同时它还绕着它的中轴进行旋转,这个就叫做旋进。最后,这个陀螺还会上下摆动,这个倾角就叫做它的点头角.这三个分别划分到不同的参考系中,都是一个旋转角。只有旋进是一个合法的旋转操作,并且通常只有旋进可以用一个基于空间的矩阵所表示。(翻译有问题?这个不太理解)
万向节类比 
 Left: A three axes
z-
x-
z
gimbal where the external frame and external axis
x are not shown and axes
Yare perpendicular to each gimbal ring.
Right: A simple diagram showing the Euler angles and where the axes
Y of intermediate frames are located.
Left: A three axes
z-
x-
z
gimbal where the external frame and external axis
x are not shown and axes
Yare perpendicular to each gimbal ring.
Right: A simple diagram showing the Euler angles and where the axes
Y of intermediate frames are located.
我们假设有一系列的参考系,可以在之前移动的基础上分别只在一个角度上进行旋转, 类似一个万向节,这里会存在一个外部的固定参考系,一个最终参考系和两个在中间的被叫做“中间参考系”的参考系。这两个像悬浮环的、在中间的参考系可以让最终的参考系达到任何一个方向。 这样,每个欧拉旋转对应一个环,与剩下的环保持独立。
中间参考系 悬浮环表示中间参考系,他们也可以被静态的定义,分别在x,y,z轴上有向量i,j,k,在XYZ上有向量I,J,K,N在交轨线上,一些中间参考系可以用向量叉乘的形式进行定义如下: 初始状态: [i,j,k] (k = i × j)第一个参考系: [N,k × N,k]第二个参考系: [N,K × N,K]最终参考系: [I,J,K] 这些中间参考系和那些悬浮环是等价的,其中一个环转动,最终的方向便会产生变动。这证明了: 通过组合这三个旋转,原始参考系可以被旋转到与任何一个目标参考系.这些旋转角就是目标参考系的欧拉角. 翻译未完,后续会接着进行翻译,并对内容加深理解,修正文章中的错误翻译。 |
【本文地址】