VARMA模型的原理与实现

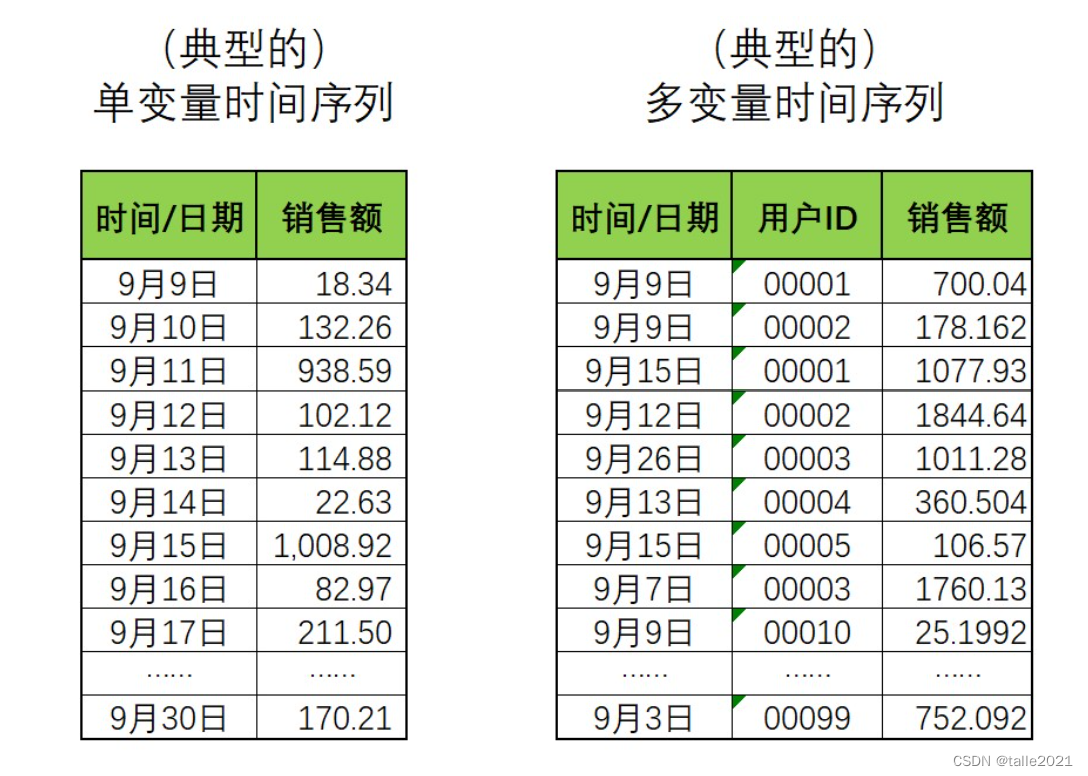
​ 在现实和竞赛中，时序数据往往是多变量时间序列，我们往往需要借助除了时间之外的变量的帮助来完成预测。比如，如果我们需要预测居民消费支出的情况，除了和时间相关的季节变化、节日变化、文化影响等因素，销售还可能受到居民收入情况的显著影响。因此如果将居民收入也纳入研究范围，那就能够得到更精准的预测数据。可见，多变量时间序列会比较常见，也是因为实现问题更为复杂、影响因素更多的缘故。 ​ ARIMA系列模型能不能直接被用于多变量时间序列数据呢?从数值上来说是有可能的，但从应用角度来说却非常困难，有两点原因: ①ARIMA系列模型的数学过程是基于单变量时间序列设计的，单变量时间序列中唯一的影响因素就是时间，但多变量时间序列数据会同时受到时间和其他重要因子的影响，因此ARIMA系列模型很有可能会忽略掉时间之外的重要因子，从而导致模型效果很糟糕。 ​ ②ARIMA模型要求时间序列数据必须是按时间顺序排列、时间不能有重复、时间间隔一致的，但多变量时间序列数据从逻辑上明显无法满足这个要求，因为多变量数据是由多个索引共同决定唯一标签值的，因此时间索引必然有重复，也不能按顺序排列。

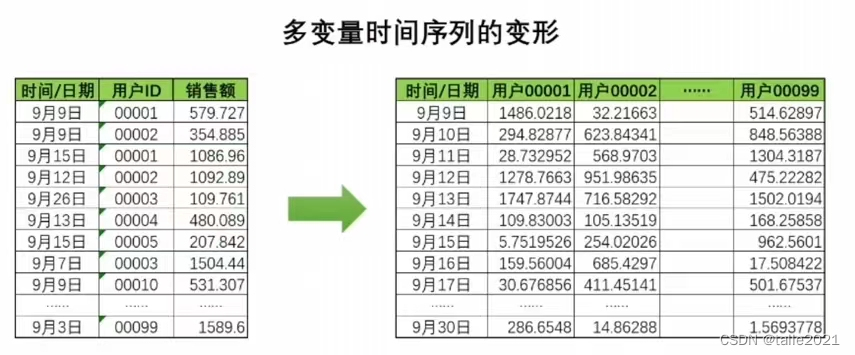
转换思路让多变量时间序列数据被转变成ARIMA模型可以处理的形式，例如，如果将用户的购买数据拆开、将每个用户的消费额按时间顺序整理出一列，那这每列数据都满足单变量时间序列的基本要求(时间顺序从前向后、没有重复的时间、时间间隔均匀等等)。如此，多变量时间序列就变为了多个单变量时间序列，而SARIMAX系列模型就可以被用于该数据的每一列来进行建模了。

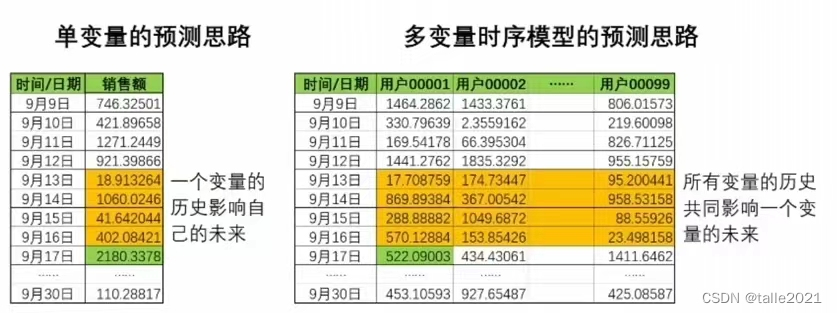
​ 在统计学中，常常以上图右侧的方式来理解多变量时间序列数据。在这种数据形式下，任意一列都是单变量的时间序列，每个列就是一个变量，而这些列的组合共同构建了多变量时间序列数据。现在的情况中涉及到99个用户，因此在这个多变量时间序列中变量的数量为99，即在一个时间点下需要求解99个值。 ​ 在单变量时间序列中，一个时间点下只需要求解一个值，而在多变量时间序列中，一个时间点下会需要求解多个值，并且，不同变量之间的值应该是会互相影响的，否则没有必要强行组成多变量时序数据，但单变量时序模型只能处理一个变量和自己历史数据的关系，却不能处理变量与变量之间的联系。可见，多变量时序数据之间的联系更复杂，拟合策略需要更多深度。 ​ 如何拟合这些更复杂的关系呢?不同的模型可能采用不同的策略，最经典、同时也最容易理解的两种策略如下: 策略1:模型融合。将多变量时间序列变形为多个单变量时间序列，再拟合这些单变量时间序列模型之间的关系。现在我们有99个变量，那我们可以针对每个变量在9月9日-9月30日之内的数据进行建模，最终获得99个模型。在此基础上，我们只需要再针对99个模型之间的关系进行建模，对这99个横型的结果进行融合，就可以对多变量时间序列进行训纺和预测了。这种傻瓜式的方法很简单也很有效，但是计算压力巨大，并且最终用于融合的模型可能变得异常复杂。 第路2:拓展ARIMA系列模型的假设，直接跨变量建立当前时间点上的值与所有历史时间点上的值的关联。如下图所示，ARIMA模型假设一个变量的未来是由该变量的历史决定的，而我们可以将该假设拓展至所有变量：一个变量的未来是由该变量自己和所有其他变量的历史共同决定的。只要求解出未来的值和多个变量上的历史值之间的系数，就可以拟合变量与自身关系的同时、也拟合出变量之间的关系。大部分统计学模型使用了这样的思路。

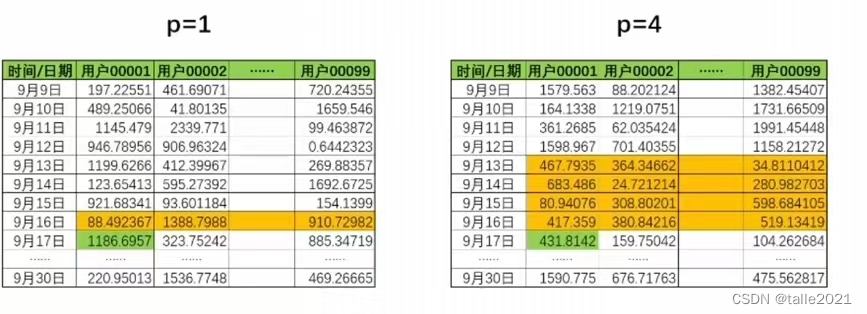
​ 在统计学、机器学习和深度学习领域中存在大量能够解决多变量时序问题的算法，包括下面这些常见的时间序列模: ◒向量自回归模型(VAR) ◒向量自回归移动平均模型(VARMA) ◒向量自回归移动平均与外生变量模型(VARMAX) ◒向量误差校正模型(VECM) ◒联合ARIMA-VAR楼型 ◒贝叶斯结构时间序列模型 ◒动态因子模型 ◒状态空间模型(卡尔曼滤波) ◒深度学习模型，如LSTM，GRU和卷积神经网络(CNN)等 ​ 在这之中，VAR模型是从AR模型改造而来，VARMA模型是从ARMA横型改造而来，他们通过拓展AR和ARMA模型来进行建模。具体地来说，这两个模型能够跨变量建立联系，直接假设当前时间点上的值不止与自己过去的值有关，也与其他变量过去的值有关，从而能够一次性建立跨变量跨序列的模型。

VAR模型是在AR模型基础上拓展出的模型，它的本质是可以对多变量时间序列进行预测的AR模型。因此VAR模型满足AR模型的一切前提假设，同时也与AR模型共享大部分数学公式和运算方法，并在此基础上发展出了三类VAR模型: 精简型VAR (Reduced VAR models)，递归性VAR (ecursive VARmodels)以及结构型VAR (Structural VAR models)，下面将以精简型VAR为例来了解VAR模型。 AR模型相信一个时间点上的标签值可以由过去某个时间段内的所有时间点上的标签值线性组合后构成(实际就是加权求和)，因此对于一个AR§模型，有如下公式: y t = c + β 1 y t − 1 + β 2 y t − 2 + . . . + β p y t − p y_{t}=c+\beta_{1}y_{t-1}+\beta_{2}y_{t-2}+...+\beta_{p}y_{t-p} yt​=c+β1​yt−1​+β2​yt−2​+...+βp​yt−p​ 在该公式当中， y t y_{t} yt​是时间点 t t t上的标签， y t − 1 y_{t-1} yt−1​是时间点 t − 1 t-1 t−1上的标签， c c c是常数项， z t z_{t} zt​则表示时间点 t t t上的白噪音。 假设现在有一个多变量时间序列，除了时间之外还涉及到k个变量(假设，是k个用户)，一个用户和一个时间点共同决定了该时间点上的值，那此时一个精简型VAR§模型的数学公式为: y t = c + B 1 y t − 1 + B 2 y t − 2 + . . . + B p y t − p \pmb{y_{t}=c+B{1}y_{t-1}+B{2}y_{t-2}+...+B{p}y_{t-p}} yt​=c+B1yt−1​+B2yt−2​+...+Bpyt−p​ 其中， y t \pmb{y_{t}} yt​是k个变量在时间点时的标签组成的向量，一般结构为(k,)，一般可表示为 [ y ( t , 1 ) , y ( t , 2 ) , y ( t , 3 ) . . . y ( t , k ) ] . T [y_{(t,1)},y_{(t,2)},y_{(t,3)}...y_{(t,k)}].T [y(t,1)​,y(t,2)​,y(t,3)​...y(t,k)​].T

很明显，该公式可以一次性求解出时间 t t t下的k个值。在该公式中， c c c与 z t z_{t} zt​也都是形如(k,)的向量，而$$则是系数矩阵，每个矩阵中包合变量与变量自身、变量与变量之间的系数，一般形状为(k.k)。

假设现在VAR模型中的p为1，即 y t y_{t} yt​只与历史前一天的值有关，并且现在变量的数目为2，则 y t y_{t} yt​为可表示为: y t = c + B 1 ∗ y t − 1 + z t [ y ( t , 1 ) y ( t , 2 ) ] = [ c ( 1 ) c ( 2 ) ] + [ β 1 ( 11 ) β 1 ( 12 ) β 1 ( 21 ) β 1 ( 22 ) ] ∗ [ y ( t − 1 , 1 ) y ( t − 1 , 2 ) ] + [ z ( t , 1 ) z ( t , 2 ) ] \pmb{y_{t}=c+B{1}*y_{t-1}+z_{t}}\\ \begin{bmatrix} y_{(t,1)} \\ y_{(t,2)} \\ \end{bmatrix}=\begin{bmatrix} c_{(1)} \\ c_{(2)} \\ \end{bmatrix}+ \begin{bmatrix} \beta1_{(11)} & \beta1_{(12)} \\ \beta1_{(21)} & \beta1_{(22)} \\ \end{bmatrix}* \begin{bmatrix} y_{(t-1,1)} \\ y_{(t-1,2)} \\ \end{bmatrix}+ \begin{bmatrix} z_{(t,1)} \\ z_{(t,2)} \\ \end{bmatrix} yt​=c+B1∗yt−1​+zt​[y(t,1)​y(t,2)​​]=[c(1)​c(2)​​]+[β1(11)​β1(21)​​β1(12)​β1(22)​​]∗[y(t−1,1)​y(t−1,2)​​]+[z(t,1)​z(t,2)​​] 其中， β \beta β后的大数字1指向的是时间间隔，而小数字(11)和(12)等则代表变量的序号，因此 β 1 ( 11 ) \beta1_{(11)} β1(11)​展示了变量1与上一个时间点上的自己之间的关系， β 1 ( 12 ) \beta1_{(12)} β1(12)​展示了变量1与上一个时间点上的变量2之间的关系。假设模型变得更加复杂，那 y t − 2 y_{t-2} yt−2​前的 β \beta β就不再是 β 1 \beta_{1} β1​，而是 β 2 \beta_{2} β2​了。

需要注意的是，当 B 1 ∗ y t − 1 \pmb{B_{1}*y_{t-1}} B1​∗yt−1​的部分相乘后可以得到: [ β 1 ( 11 ) β 1 ( 12 ) β 1 ( 21 ) β 1 ( 22 ) ] ∗ [ y ( t − 1 , 1 ) y ( t − 1 , 2 ) ] = [ β 1 ( 11 ) y ( t − 1 , 1 ) + β 1 ( 12 ) y ( t − 1 , 2 ) β 1 ( 21 ) y ( t − 1 , 1 ) + β 1 ( 22 ) y ( t − 1 , 2 ) ] \begin{bmatrix} \beta1_{(11)} & \beta1_{(12)} \\ \beta1_{(21)} & \beta1_{(22)} \\ \end{bmatrix}* \begin{bmatrix} y_{(t-1,1)} \\ y_{(t-1,2)} \\ \end{bmatrix}= \begin{bmatrix} \beta1_{(11)}y_{(t-1,1)} + \beta1_{(12)}y_{(t-1,2)} \\ \beta1_{(21)}y_{(t-1,1)} +\beta1_{(22)}y_{(t-1,2)} \\ \end{bmatrix} [β1(11)​β1(21)​​β1(12)​β1(22)​​]∗[y(t−1,1)​y(t−1,2)​​]=[β1(11)​y(t−1,1)​+β1(12)​y(t−1,2)​β1(21)​y(t−1,1)​+β1(22)​y(t−1,2)​​] 所以实际上的 y t \pmb{y_{t}} yt​等于： y t = c + B 1 ∗ y t − 1 + z t [ y ( t , 1 ) y ( t , 2 ) ] = [ c ( 1 ) + β 1 ( 11 ) y ( t − 1 , 1 ) + β 1 ( 12 ) y ( t − 1 , 2 ) + z ( t , 1 ) c ( 2 ) + β 1 ( 21 ) y ( t − 1 , 1 ) + β 1 ( 22 ) y ( t − 1 , 2 ) + z ( t , 2 ) ] \pmb{y_{t}=c+B{1}*y_{t-1}+z_{t}}\\ \begin{bmatrix} y_{(t,1)} \\ y_{(t,2)} \\ \end{bmatrix}= \begin{bmatrix} c_{(1)}+\beta1_{(11)}y_{(t-1,1)} + \beta1_{(12)}y_{(t-1,2)}+z_{(t,1)} \\ c_{(2)}+\beta1_{(21)}y_{(t-1,1)} +\beta1_{(22)}y_{(t-1,2)}+z_{(t,2)} \\ \end{bmatrix} yt​=c+B1∗yt−1​+zt​[y(t,1)​y(t,2)​​]=[c(1)​+β1(11)​y(t−1,1)​+β1(12)​y(t−1,2)​+z(t,1)​c(2)​+β1(21)​y(t−1,1)​+β1(22)​y(t−1,2)​+z(t,2)​​] ​ 这种形式也可以被理解为建立了两个跨变量的AR模型，再共同组合形成最终的大模型。在现在的情况下，每个AR模型中影响未来的不是只有当前变量过去的值，也有其他变量过去的值，这就让拟合多变量时间序列成为可能。 ​ 基于VAR模型的理解，VARMA模型是在ARMA模型的基础上改进而来，在VARMA模型中，当前的值会受当前变量过去的值影响、也会受到其他变最过去的值影响。 y t = μ + B 1 y t − 1 + . . . + B p y t − p + ϵ t + θ 1 ϵ t − 1 + . . . + θ q ϵ t − q \pmb{y_{t}=\mu+B{1}y_{t-1}+...+B{p}y_{t-p}+\epsilon_{t}+\theta1\epsilon_{t-1}+...+\theta{q}\epsilon_{t-q}} yt​=μ+B1yt−1​+...+Bpyt−p​+ϵt​+θ1ϵt−1​+...+θqϵt−q​ ​ 很明显，当p=0时实现VMA模型，当q =0时实现VAR模型，当p和q都不为0时实现的就是VARMA模型。值得一提的是，VARIMA模型比较少见，常见的是VARMA和VARMAX等模型，这主要是因为ARIMA模型中的字母I其实代表用于处理非平稳数据的差分技术，但这一技术很难被应用到多变量时间序列当中。如果我们希望多变量时序数据具有平稳性，那就需要一次性对所有变量的数据都进行不同程度的差分，并最终保证所有变量的联合概率分布处于平稳状态。这一状态在实际使用算法时几平不可能达到，因此大部分现实情况下我们可能会忽略不平稳性在多变量时序数据中带来的影响。也因此，多变量时序数据下我们就很少使用差分技术，也就很少使用字母i了。 ​ 在统计学领域，VAR和VARMA模型是应用最广泛的多变量时序模型，这两个模型思路清晰简单、并且直接在原本的AR和ARMA模型上改进，因此他们的使用方式、注意事项、缺点改善等也都可借鉴AR和ARMA模型经验。同时，交叉组合不同变量并拟合他们之间的关系可以找出远超人工想象的奇妙联系，因此VAR和VARMA模型在许多场合下都可以提升模型表现。不过，这一系类模型也有明显的缺点，包括:

​ ①由于要计算不同变量之间的交叉组合关系，VAR和VARMA模型可能变得复杂度太高、计算量过大，这会导致寻找超参数、抗过拟合等问题变得更加复杂和困难。

​ ②由于是在AR和ARMA模型基础上改进，因此VAR和VARMA模型也需要满足原始模型的严格条件例如，残差需要正态分布、相互独立。例如，残差需要正态分布、相互独立。例如，各项检验需要严格通过等等。

​ ③根据实验的结果，VARMA模型对异常值和离群值极其敬感，因此也可能导致非常糟糕的结果。

75 rows × 3 columns

​ 这张summary表单中最后的Eror Covariance Matrix，就是列差的协方差拍阵，ARIMA模型要求残差项相互独立目满足正态分布，VARMA模型则要求多变量下的残差要满足均值向量为0的联合正态分布、且相互独立，因此才会提供协方差矩阵供我们判断不同变量的残差之间的关联程变。例如，残差协方差矩阵的第一列coef就代表了每个变量的方差，以及变量之间的协方差系数。在当前状况下办方差系数越靠近0越好。

​ 同时，在协方差短阵中执行的检验也是针对每一个方差和协方差值的单变量检验，也就展当前值息否为0的检验。 ​ ◉单变量检验的原假设(H0):当前方差/协方差值coef为0 ​ ◉单变量检验的备择假设(H1):当前方差/协方差值coef不为0

如果有任意项的p值大于规定的显著性水平a(0.05或0.01)，就说明当前的方差/协方差值可能为0，当前项的系数没能拒绝原假设、无法通过显著性检验，模型对当前给出的非0值没有足够的信心。

​ 在VARMA模型中还可以设置“外生变量”(Exogenous series)，，外生变量是会影响到时间序列数居，但是却不参与建横的变量。一个序列不参与建模，证明我们无需针对这个序列进行未来的预测，但是这个序列却会影响到我们要预测的时序数据。比如，当我们要预测标准普尔指数的变化时，典型的外生变量就是政府政策。我们并不想预测下一个时间点的政府政第会如何变化，但政府政第的变化确实会严重影响我们想要预则的标准普尔旨数。VARMA模型允许我们在建模时输入不止一个外生变量，这句以很大程度上地帮助我们提升横型的精度。

从AlC和BIC的表现来看，预测变量的数目以及外生变量存在与否会很大程度上改变模型的表现。当存在外生变量的寸候，我们还可以绘制外生变量和预测变量的图像，来观察外生变量如何影响预测变量。