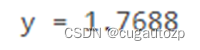数值分析（四） Hermite（埃尔米特）插值法及matlab代码

  本篇为插值法专栏第四篇内容讲述，此章主要讲述 Hermite（埃尔米特）插值法及matlab代码，其中也给出详细的例子让大家更好的理解Hermite插值法 提示 之前已经介绍牛顿插值法和三次样条插值，如果没看过前两篇的可以点击以下链接阅读

  在许多实际应用中，不仅要求函数值相等，而且要求若干阶导数也相等。

  定义：满足函数值相等且导数也相等的插值方法 f ( x ) ≈ φ ( x ) f(x) \approx \varphi (x) f(x)≈φ(x)， φ ( x i ) = f ( x i ) ( i = 0 , 1 , … , n ) \varphi ({x_i}) = f({x_i}) (i=0,1,\ldots ,n) φ(xi​)=f(xi​)(i=0,1,…,n) φ ′ ( x i ) = f ′ ( x i ) \varphi '({x_i}) = f'({x_i}) φ′(xi​)=f′(xi​) φ ( 2 ) ( x i ) = f ( 2 ) ( x i ) \varphi ^{(2)} ({x_i}) = f ^{(2)} ({x_i}) φ(2)(xi​)=f(2)(xi​) ⋮ \vdots ⋮ φ ( m ) ( x i ) = f ( m ) ( x i ) \varphi ^{(m)} ({x_i}) = f ^{(m)} ({x_i}) φ(m)(xi​)=f(m)(xi​)

定理：设 f ( x ) ∈ C n [ a , b ] , x 0 , . . . , x n f(x) \in {C^n}[a,b],{x_0},...,{x_n} f(x)∈Cn[a,b],x0​,...,xn​ 为 [ a , b ] [a,b] [a,b] 上的互异节点，则 f [ x 0 , . . . , x n ] f[{x_0},... ,{x_n}] f[x0​,...,xn​] 是其变量的连续函数

  注意： 差商知识不清楚的话可以看之前这篇 数值分析（一）牛顿插值法 中有对差商详细的讲解 f [ x 0 , x 0 ] = lim ⁡ x 1 → x 0 f [ x 0 , x 1 ] = f ( x 1 ) − f ( x 0 ) x 1 − x 0 = f ′ ( x 0 ) f[{x_0},{x_0}] = \mathop {\lim }\limits_{{x_1} \to {x_0}} f[{x_0},{x_1}] = \frac{{f({x_1}) - f({x_0})}}{{{x_1} - {x_0}}} = f'({x_0}) f[x0​,x0​]=x1​→x0​lim​f[x0​,x1​]=x1​−x0​f(x1​)−f(x0​)​=f′(x0​) f [ x 0 , x 0 , x 0 ] = lim ⁡ x 1 → x 0 x 2 → x 0 f [ x 0 , x 1 , x 2 ] = 1 2 ! f ′ ′ ( x 0 ) f[{x_0},{x_0},{x_0}] = \mathop{\lim }\limits_{{x_1} \to {x_0}\\{{x_2} \to {x_0}}}f[{x_0},{x_1},{x_2}] = \frac{1}{{2!}}f''({x_0}) f[x0​,x0​,x0​]=x1​→x0​x2​→x0​lim​f[x0​,x1​,x2​]=2!1​f′′(x0​) 一般 n n n 阶重节点差商定义为： f [ x 0 , x 0 , ⋯   , x 0 ] = lim ⁡ x i → x 0 f [ x 0 , x 1 , ⋯   , x n ] = 1 n ! f ( n ) ( x 0 ) f[{x_0},{x_0},\cdots,{x_0}] = \mathop{\lim }\limits_{{x_i} \to {x_0}}f[{x_0},{x_1},\cdots,{x_n}] = \frac{1}{{n!}}f^{(n)}({x_0}) f[x0​,x0​,⋯,x0​]=xi​→x0​lim​f[x0​,x1​,⋯,xn​]=n!1​f(n)(x0​)

  在Newton插值公式中，令 x i → x 0 , i = 1 , ⋯   , n x_i \to x_0, i = 1, \cdots, n xi​→x0​,i=1,⋯,n，则 N n ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + ⋯ + f [ x 0 , x 1 , ⋯   , x n ] ∏ i = 1 n − 1 ( x − x i ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n N_n(x) = f(x_0)+f[x_0, x_1](x - x_0)+ \cdots + f[x_0, x_1, \cdots, x_n]\prod_{i=1 }^{n-1} (x-x_i) \\ = f(x_0) + f'(x_0)(x-x_0)+ \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n Nn​(x)=f(x0​)+f[x0​,x1​](x−x0​)+⋯+f[x0​,x1​,⋯,xn​]i=1∏n−1​(x−xi​)=f(x0​)+f′(x0​)(x−x0​)+⋯+n!f(n)(x0​)​(x−x0​)n

担心有些同学看不懂推导，解释一下如何转化为第二个等式（即，Taylor 插值多项式）：

将1.1中讲述的重节点差商 带入Newton插值公式中： lim ⁡ x i → x 0 f [ x 0 , x 1 , ⋯   , x n ] = 1 n ! f ( n ) ( x 0 ) \mathop{\lim }\limits_{{x_i} \to {x_0}}f[{x_0},{x_1},\cdots,{x_n}]=\frac{1}{{n!}}f^{(n)}({x_0}) xi​→x0​lim​f[x0​,x1​,⋯,xn​]=n!1​f(n)(x0​)所有的 x i → x 0 x_i \to x_0 xi​→x0​，所以 ∏ i = 1 n − 1 ( x − x i ) \prod_{i=1 }^{n-1} (x-x_i) ∏i=1n−1​(x−xi​) 就变成了 ( x − x 0 ) n (x-x_0)^n (x−x0​)n

插值余项 R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} Rn​(x)=(n+1)!f(n+1)(ξ)​(x−x0​)n+1

  一般来说，给定 m + 1 m+1 m+1 个插值条件，就可以构造出一个 m m m 次Hermite 插值多项式，接下来介绍两个典型的Hermite插值：三点三次 Hermite插值 和 两点三次 Hermite 插值

  插值节点： x 0 ， x 1 ， x 2 x_0，x_1， x_2 x0​，x1​，x2​   插值条件： P ( x i ) = f ( x i ) ， i = 0 , 1 , 2 ， P ′ ( x 1 ) = f ′ ( x 1 ) P(x_i) = f(x_i)，i=0,1,2，P'(x_1) = f'(x_1) P(xi​)=f(xi​)，i=0,1,2，P′(x1​)=f′(x1​)

  设： P ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) + A ( x − x 0 ) ( x − x 1 ) ( x − x 2 ) P(x) = f(x_0) + f[x_0,x_1](x-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)+A(x-x_0)(x-x_1)(x-x_2) P(x)=f(x0​)+f[x0​,x1​](x−x0​)+f[x0​,x1​,x2​](x−x0​)(x−x1​)+A(x−x0​)(x−x1​)(x−x2​) 将 P ′ ( x 1 ) = f ′ ( x 1 ) P'(x_1) = f'(x_1) P′(x1​)=f′(x1​)代入可得 A = f ′ ( x 1 ) − f [ x 0 , x 1 ] − f [ x 0 , x 1 , x 2 ] ( x 1 − x 0 ) ( x 1 − x 0 ) ( x 1 − x 2 ) A = \frac{f'(x_1)-f[x_0,x_1] - f[x_0,x_1,x_2](x_1-x_0)}{(x_1-x_0)(x_1-x_2)} A=(x1​−x0​)(x1​−x2​)f′(x1​)−f[x0​,x1​]−f[x0​,x1​,x2​](x1​−x0​)​ 由于 x 0 , x 1 , x 2 x_0,x_1,x_2 x0​,x1​,x2​是 R ( x ) R(x) R(x)的零点，且 x 1 x_1 x1​是二重零点，故可设，余项公式： R ( x ) = f ( x ) − P ( x ) = k ( x ) ( x − x 0 ) ( x − x 1 ) 2 ( x − x 2 ) R(x) = f(x) - P(x) = k(x)(x-x_0)(x-x_1)^2(x-x_2) R(x)=f(x)−P(x)=k(x)(x−x0​)(x−x1​)2(x−x2​)与 Lagrange 插值余项公式的推导过程类似，可得 R ( x ) = f ( 4 ) ( ξ x ) 4 ! ( x − x 0 ) ( x − x 1 ) 2 ( x − x 2 ) R(x) = \frac{f^{(4)}(\xi_x)}{4!}(x-x_0)(x-x_1)^2(x-x_2) R(x)=4!f(4)(ξx​)​(x−x0​)(x−x1​)2(x−x2​) 其中 ξ x \xi_x ξx​ 位于由 x 0 , x 1 , x 2 x_0, x_1, x_2 x0​,x1​,x2​和 x x x所界定的区间内

  插值节点： x 0 ， x 1 x_0，x_1 x0​，x1​   插值条件： P ( x i ) = f ( x i ) = y i ， P ′ ( x i ) = f ′ ( x i ) = m i ， i = 0 , 1 P(x_i) = f(x_i)=y_i，P'(x_i) = f'(x_i)=m_i，i=0,1 P(xi​)=f(xi​)=yi​，P′(xi​)=f′(xi​)=mi​，i=0,1

  模仿Lagrange 多项式的思想，设 H 3 ( x ) = y 0 α 0 ( x ) + y 1 α 1 ( x ) + m 0 β 0 ( x ) + m 1 β 1 ( x ) H_3(x) = y_0\alpha_0(x)+y_1\alpha_1(x)+m_0\beta_0(x)+m_1\beta_1(x) H3​(x)=y0​α0​(x)+y1​α1​(x)+m0​β0​(x)+m1​β1​(x)其中 α 0 ( x ) , α 1 ( x ) , β 0 ( x ) , β 1 ( x ) \alpha_0(x), \alpha_1(x), \beta_0(x), \beta_1(x) α0​(x),α1​(x),β0​(x),β1​(x)均为3次多项式，且满足 α j ( x i ) = δ i j , α j ′ ( x i ) = 0 , β j ( x i ) = 0 , β j ′ ( x i ) = δ j i ( i , j = 0 , 1 ) \alpha_j(x_i) = \delta_{ij}, \alpha'_j(x_i)=0,\\ \beta_j(x_i)=0, \beta'_j(x_i) = \delta_{ji} \\ (i, j =0, 1) αj​(xi​)=δij​,αj′​(xi​)=0,βj​(xi​)=0,βj′​(xi​)=δji​(i,j=0,1)

上述中的 δ i j \delta_{ij} δij​表达式在Lagrange多项式中提到过，怕有些同学忘了这里帮忙回顾一下 l k ( x i ) = δ k i = { 1 ( i = k ) 0 ( i ≠ k ) l_k(x_i) = \delta_{ki} = \left \{\begin{matrix}1&(i=k) \\ 0&(i \ne k)\end{matrix}\right. lk​(xi​)=δki​={10​(i=k)(i=k)​

将插值条件代入立即可得 α 0 ( x ) \alpha_0(x) α0​(x)求解过程

  Step 1：根据前面可以得到： α 0 ( x 0 ) = 1 , α 0 ′ ( x 0 ) = 0 , α 0 ( x 1 ) = 0 , α 0 ′ ( x 1 ) = 0 \alpha_0(x_0) = 1, \alpha'_0(x_0)=0, \alpha_0(x_1) = 0, \alpha'_0(x_1)=0 α0​(x0​)=1,α0′​(x0​)=0,α0​(x1​)=0,α0′​(x1​)=0

  Step 2：由上面提到过 α 0 ( x ) , α 1 ( x ) , β 0 ( x ) , β 1 ( x ) \alpha_0(x), \alpha_1(x), \beta_0(x), \beta_1(x) α0​(x),α1​(x),β0​(x),β1​(x)都是3次多项式， α 0 ( x 1 ) = 0 , α 0 ′ ( x 1 ) = 0 \alpha_0(x_1) = 0, \alpha'_0(x_1)=0 α0​(x1​)=0,α0′​(x1​)=0，根据以上条件可以构造函数为： α 0 ( x ) = ( a x + b ) ( x − x 1 x 0 − x 1 ) 2 \alpha_0(x) = (ax + b)(\frac{x-x_1}{x_0-x_1})^2 α0​(x)=(ax+b)(x0​−x1​x−x1​​)2   Step 3：将 α 0 ( x 0 ) = 1 , α 0 ′ ( x 0 ) = 0 \alpha_0(x_0) = 1, \alpha'_0(x_0) = 0 α0​(x0​)=1,α0′​(x0​)=0 代入上式，可以求解得到 a = − 2 x 0 − x 1 , b = 3 x 0 − x 1 x 0 − x 1 = 1 + 2 x 0 x 0 − x 1 a = -\frac{2}{x_0-x_1}, b = \frac{3x_0-x_1}{x_0-x_1} = 1+ \frac{2x_0}{x_0-x_1} a=−x0​−x1​2​,b=x0​−x1​3x0​−x1​​=1+x0​−x1​2x0​​   Step 4：将求得出来的 a , b a, b a,b 代入到构造的函数 α 0 ( x ) \alpha_0(x) α0​(x) 中，即得： α 0 ( x ) = ( 1 + 2 x − x 0 x 1 − x 0 ) ( x − x 1 x 0 − x 1 ) 2 \alpha_0(x) = (1+2\frac{x-x_0}{x_1-x_0})(\frac{x-x_1}{x_0-x_1})^2 α0​(x)=(1+2x1​−x0​x−x0​​)(x0​−x1​x−x1​​)2

注意：我在推公式的过程感觉是2前面是个减号(很容易出现自己推导和给出的不一致)，我仔细一看发现是这么一回事，那么我来把省略的一些步骤给他详细写一下 a x + b = − 2 x x 0 − x 1 + 1 + 2 x 0 x 0 − x 1 = 1 − 2 x − x 0 x 0 − x 1 = 1 + 2 x − x 0 x 1 − x 0 ax+b = -\frac{2x}{x_0-x_1}+1+ \frac{2x_0}{x_0-x_1} = 1 - 2\frac{x-x_0}{x_0-x_1} = 1 + 2\frac{x-x_0}{x_1-x_0} ax+b=−x0​−x1​2x​+1+x0​−x1​2x0​​=1−2x0​−x1​x−x0​​=1+2x1​−x0​x−x0​​才发现将-放到了分母

同理： α 1 ( x ) = ( 1 + 2 x − x 1 x 0 − x 1 ) ( x − x 0 x 1 − x 0 ) 2 \alpha_1(x) = (1+2\frac{x-x_1}{x_0-x_1})(\frac{x-x_0}{x_1-x_0})^2 α1​(x)=(1+2x0​−x1​x−x1​​)(x1​−x0​x−x0​​)2

类似得可以得到： β 0 ( x ) = ( x − x 0 ) ( x − x 1 x 0 − x 1 ) 2 \beta_0(x) = (x-x_0)(\frac{x-x_1}{x_0-x_1})^2 β0​(x)=(x−x0​)(x0​−x1​x−x1​​)2 β 1 ( x ) = ( x − x 1 ) ( x − x 0 x 1 − x 0 ) 2 \beta_1(x) = (x-x_1)(\frac{x-x_0}{x_1-x_0})^2 β1​(x)=(x−x1​)(x1​−x0​x−x0​​)2

满足插值条件 P ( x 0 ) = f ( x 0 ) = y 0 ， P ′ ( x 0 ) = f ′ ( x 0 ) = m 0 P ( x 1 ) = f ( x 1 ) = y 1 ， P ′ ( x 1 ) = f ′ ( x 1 ) = m 1 P(x_0) = f(x_0)=y_0，P'(x_0) = f'(x_0)=m_0 \\ P(x_1) = f(x_1)=y_1，P'(x_1) = f'(x_1)=m_1 P(x0​)=f(x0​)=y0​，P′(x0​)=f′(x0​)=m0​P(x1​)=f(x1​)=y1​，P′(x1​)=f′(x1​)=m1​ 的三次Hermite插值多项式为 H 3 ( x ) = y 0 ( 1 + 2 x − x 0 x 1 − x 0 ) ( x − x 1 x 0 − x 1 ) 2 + y 1 ( 1 + 2 x − x 1 x 0 − x 1 ) ( x − x 0 x 1 − x 0 ) 2 + m 0 ( x − x 0 ) ( x − x 1 x 0 − x 1 ) 2 + m 1 ( x − x 1 ) ( x − x 0 x 1 − x 0 ) 2 H_3(x) = y_0(1+2\frac{x-x_0}{x_1-x_0})(\frac{x-x_1}{x_0-x_1})^2+y_1 (1+2\frac{x-x_1}{x_0-x_1})(\frac{x-x_0}{x_1-x_0})^2 \\ +m_0(x-x_0)(\frac{x-x_1}{x_0-x_1})^2+m_1(x-x_1)(\frac{x-x_0}{x_1-x_0})^2 H3​(x)=y0​(1+2x1​−x0​x−x0​​)(x0​−x1​x−x1​​)2+y1​(1+2x0​−x1​x−x1​​)(x1​−x0​x−x0​​)2+m0​(x−x0​)(x0​−x1​x−x1​​)2+m1​(x−x1​)(x1​−x0​x−x0​​)2

余项 R 3 ( x ) = f ( 4 ) ( ξ x ) 4 ! ( x − x 0 ) 2 ( x − x 1 ) 2 R_3(x) = \frac{f^{(4)}(\xi_x)}{4!}(x-x_0)^2(x-x_1)^2 R3​(x)=4!f(4)(ξx​)​(x−x0​)2(x−x1​)2其中 ξ x ∈ ( x 0 , x 1 ) \xi_x \in (x_0, x_1) ξx​∈(x0​,x1​)

  由上面 4.2 中给出了 α 0 ( x ) , α 1 ( x ) , β 0 ( x ) , β 1 ( x ) \alpha_0(x), \alpha_1(x), \beta_0(x), \beta_1(x) α0​(x),α1​(x),β0​(x),β1​(x) 的表达式，那么依次类推推导出 2 n + 1 2n+1 2n+1 次Hermite插值多项式，且条件为 H ( x i ) = f ( x i ) ， H ′ ( x i ) = f ′ ( x i ) ， ( i = 0 , 1 , ⋯   , n ) H(x_i) = f(x_i)，H'(x_i) = f'(x_i)，(i=0,1,\cdots,n) H(xi​)=f(xi​)，H′(xi​)=f′(xi​)，(i=0,1,⋯,n)   求解： α j ( x ) \alpha_j(x) αj​(x) 和 β j ( x ) \beta_j(x) βj​(x) ( j = 0 , 1 , ⋯   , n ) (j = 0,1,\cdots,n) (j=0,1,⋯,n) α j ( x ) = [ 1 − 2 ( x − x j ) ∑ k = 0 k ≠ j n 1 x j − x k ] l j 2 ( x ) \alpha_j(x) = [1-2(x-x_j)\sum_{\begin{matrix} k = 0\\ k\ne j \end{matrix}}^{n}\frac{1}{x_j-x_k}]l_j^2(x) αj​(x)=[1−2(x−xj​)k=0k=j​∑n​xj​−xk​1​]lj2​(x) β j ( x ) = ( x − x j ) l j 2 ( x ) \beta_j(x) = (x-x_j)l_j^2(x) βj​(x)=(x−xj​)lj2​(x) H 2 n + 1 ( x ) = ∑ j = 0 n [ 1 − 2 ( x − x j ) ∑ k = 0 k ≠ j n 1 x j − x k ] l j 2 ( x ) f ( x j ) + ∑ j = 0 n ( x − x j ) l j 2 ( x ) f ′ ( x j ) H_{2n+1}(x) = \sum_{j=0}^{n}[1-2(x-x_j)\sum_{\begin{matrix} k = 0\\ k\ne j \end{matrix}}^{n}\frac{1}{x_j-x_k}]l_j^2(x)f(x_j)+\sum_{j=0}^{n}(x-x_j)l_j^2(x)f'(x_j) H2n+1​(x)=j=0∑n​[1−2(x−xj​)k=0k=j​∑n​xj​−xk​1​]lj2​(x)f(xj​)+j=0∑n​(x−xj​)lj2​(x)f′(xj​)

上述中的 l j ( x ) l_j(x) lj​(x) 在 Lagrange 多项式中提到过不太清楚得同学可以去回顾一下

Matlab 版本号 2022b

主函数：

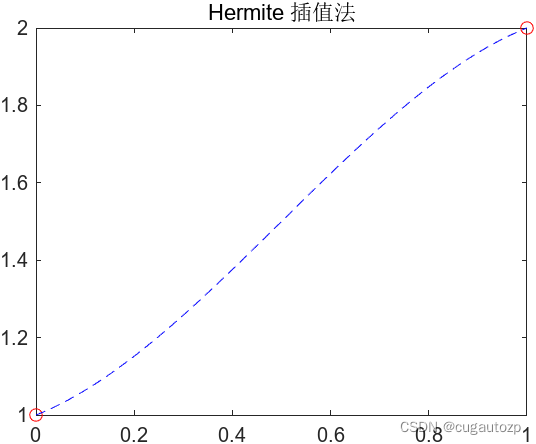
结果：

  这篇blog我推迟了1年才开始写，本应该很早就把这篇写完，由于比较忙遇到一些事情，现在重新得拾起开始撰写分享给大家，也非常感谢大家对我的关注，今年的计划也是将这个插值法专栏更新完，之后会再转换到另一个专栏的撰写。下方有专栏链接，可以订阅一下防止找不到。

专栏链接：插值法专栏，如果对你有帮助的话可以点个赞，点个订阅，我将完善此专栏