| 用格林定理求Jordan曲线包围的封闭区域的面积 | 您所在的位置:网站首页 › origin求曲线包围的面积 › 用格林定理求Jordan曲线包围的封闭区域的面积 |
用格林定理求Jordan曲线包围的封闭区域的面积
|
背景
发现很多教材讲微积分中的格林定理忽略其引申,显得粗糙。看了不同版本教材比对之后,这种感受更深了。 Green′stheorem 联系着二重积分和第二类平面曲线积分,是个漂亮的结果. 对原始定理稍作引申,不仅加深理解,在计算几何的某些算法实现中灵活应用起来也很方便。不但格林定理,散度定理也有类似的应用,让人惊讶。 定理和引申定理 ( Green's theorem, also Jordan curve theorem ): 向量场 (x,y)−→F⟨X,Y⟩ , ∂X∂y 和 ∂Y∂x 在有界单连通区间 D 上连续;D 的边界为Jordan曲线 C :r(s)=⟨x(s),y(s)⟩。则环量形式 circulation form: ∬D(∂Y∂x−∂X∂y)dxdy=∮CF⋅dr=∮C(Xdx+Ydy) 类似地有通量形式flux form: ∬D(∂X∂x+∂Y∂y)dxdy=∮CF⋅nds=∮C(Xdy−Ydx) 引申 对circulation form, 如果 (∂Y∂x−∂X∂y)=1 , 定理的公式左边就是区域 D 的面积。满足这样条件的F 有很多, 比如 ⟨0,x⟩ , ⟨−y,0⟩ , 12⟨−y,x⟩ 等等。从而有: DArea=∬Ddxdy=∮Cxdy=−∮Cydx=12∮C(xdy−ydx)适当更换 F ,⟨x,0⟩, ⟨0,y⟩ , 12⟨x,y⟩ ,可以类似得到flux form的等价的引申结果。 用户评价:使用了上面公式之后发现, A=12∮C(xdy−ydx) 比起另外两个只用了被积函数的左右一半部分的公式有独特的优越性。比如,它使得所有经过 (0,0) 的直线上的积分都为 0 (而另外两个只对坐标轴适用!),当封闭区域类似扇形时,可以只计算弯曲弧线上的积分;又如,在下面椭圆面积计算中也对被积函数有更显著的简化。Jordan曲线作为适用范围只是定理适用的充分但非必要条件。边界为封闭曲线,区域内任何点关于边界曲线的 卷绕数 都为 1 似乎更理想, 尤其是如果面积也允许有符号时; 因为这样得到的面积与曲线方向有关, 否则也有反例存在: Lemniscates of Bernoulli, 跟曲线参数方程特定的形式有关( 因为这影响曲线的走向),此时极坐标积分反而可能更好。 http://math.uga.edu/~pete/handouteight.pdf 应用案例 椭圆面积国外教科书中多讲椭圆面积的计算。大概因为这个最具有代表性。用其它方法计算都没有这个省力。 比如 C=⟨acost,bsint⟩,t∈[0,2π] 所包围的区域的面积。 格林定理的引申: 令向量场 F=12⟨−y,x⟩ , 利用定理的引申: S=12∮Cacostd(bsint)−bsintd(acost)=ab2∫02π(cos2t+sin2t)dt=πab如果用极坐标呢? 因为参数方程中的参数 t 并不是极坐标下的角度 θ, 所以变极坐标形式还是有一点点繁琐的。先写成隐函数形式: b2x2+a2y2=a2b2 再把 x=ρcosθ,y=ρsinθ 代入解出 ρ ρ(θ)=aba2sin2θ+b2cos2θ−−−−−−−−−−−−−−−√ 进而: S=∫02π∫aba2sin2θ+b2cos2θ√0ρdρdθ=12∫2π0a2b2a2sin2θ+b2cos2θdθ 再把被积函数变成 cos2θ 形式变量代换, 比如 cos2θ=1−t21+t2,θ=tan−1t , 成为有理函数积分, 结果也是 πab ,但是这里省略的那些步骤其实是比较麻烦的。说不定看到这里的同学有一半都想不起来了: 不过我刚刚专门花半小时看了下有理函数积分的教材, 所以, 我已经脱离这个行列了。 四瓣花形曲线的面积如果用一个形状更特殊, 常规方法繁琐的例子则容易给人更深的印象。 比如: ⎧⎩⎨⎪⎪x=y=cos(t)cos2(2t)−−−−−−−√4sin(t)cos2(2t)−−−−−−−√4t∈[0,2π]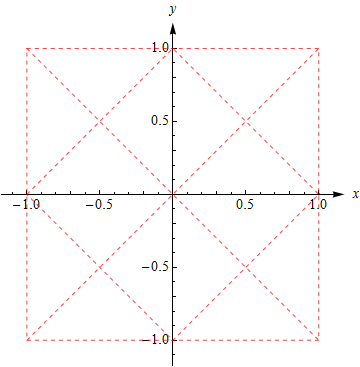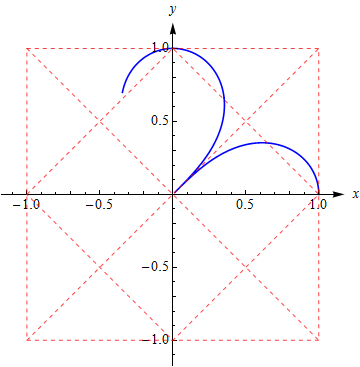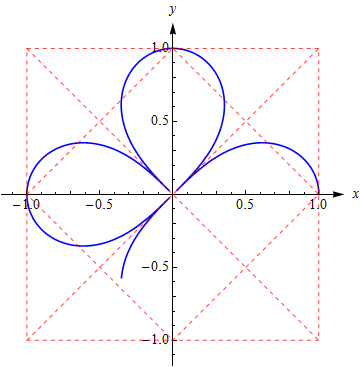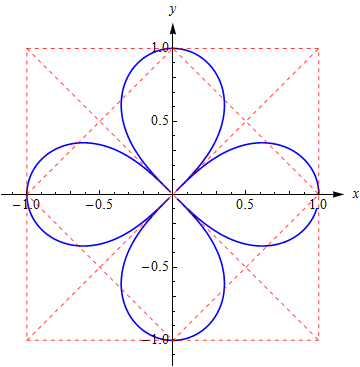
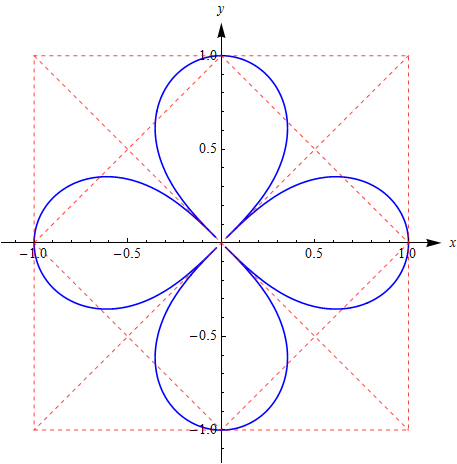 用格林定理的引申可以得到其面积恰好为
2
。 这个例子实际上用极坐标下的积分也很容易验证结果(实际上我没有验证,看上去不见得容易)。然而格林定理可以直接应用还是让人意外。
用格林定理的引申可以得到其面积恰好为
2
。 这个例子实际上用极坐标下的积分也很容易验证结果(实际上我没有验证,看上去不见得容易)。然而格林定理可以直接应用还是让人意外。
这个例子四个花瓣有公共点(0,0)应该就不算Jordan曲线了,但封闭的开区域内 卷绕数 都为 1 且曲线方向一致(如果方向相反可能有负卷绕数), 所以仍然适用格林定理;此外,四个象限中,曲线都正好等分单位正方形,这让人也感觉很好。 此外, 这个案例 ⟨sin2t,sint⟩ 也不错。 伯努利双纽线Lemniscates of Bernoulli前面提到这类曲线能否适用Green’s theorem实际上跟曲线参数方程特定的形式有关(因为这影响曲线的走向), 这里举两个例子, 同样都是 Lemniscates of Bernoulli , 但参数方程决定的曲线走向差异, 一个适用, 一个太难适用。 先说适用的: 参数方程 ⎧⎩⎨⎪⎪x=y=cos(t)cos(2t)−−−−−−√cos(2t)−−−−−−√sin(t)t∈[0,π4]∪[3π4,5π4]∪[7π4,2π] 曲线及其方向是这样的: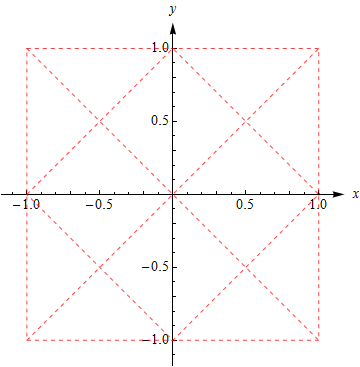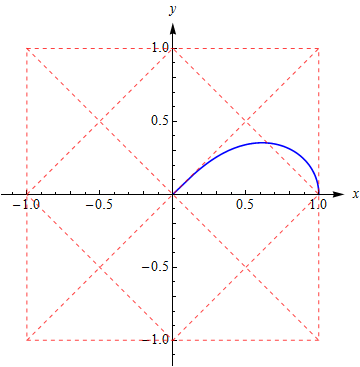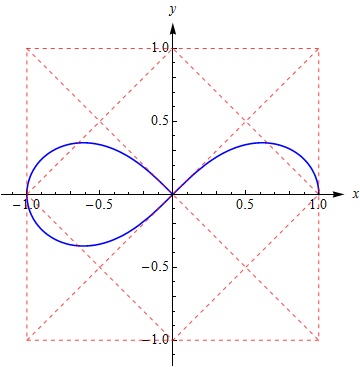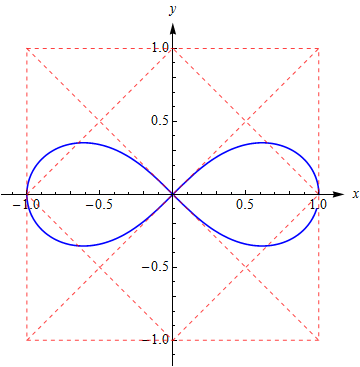 容易知道它是前面四瓣花形曲线的一半, 面积是
1
.
容易知道它是前面四瓣花形曲线的一半, 面积是
1
.
而这条曲线: ⎧⎩⎨⎪⎪⎪⎪⎪⎪x=y=343cost−245cos(2t)+10149−140cost49(5sin(2t)−7sint)140cost−149t∈[0,2π] 曲线的走向随参数 t 的增加是这样的: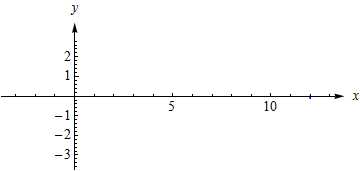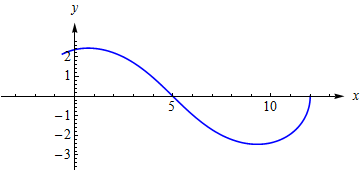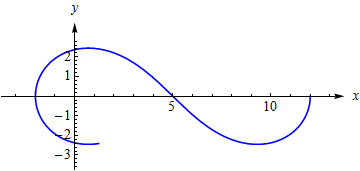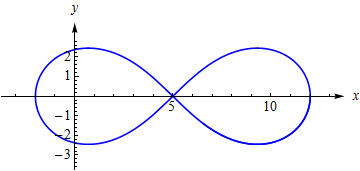 用格林公式计算面积总是正负抵消,结果为0
用格林公式计算面积总是正负抵消,结果为0
调整参数方程的形式之后用前面方法计算它的面积其实还是可以得到解析形式 751−−√−π2+cot−1(751−−√)≈48.43920 的。这类曲线可以看成可以应用格林定理的不同封闭区域之间单连通。 常拿来说事的不能用此定理的曲线参数方程为: {xy=−9sin(2t)−5sin(3t)=9cos(2t)−5cos(3t)t∈[0,2π] 刚刚计算过它的 隐函数曲线形式, 形状如: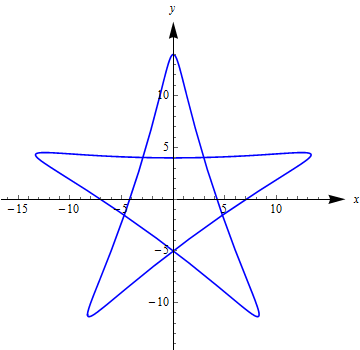
如果直接用 格林定理 则得到 87π , 跟半径 87−−√ 的圆一比较, 发现实际面积并没有圆大,显然是错误的。中心卷绕数为2、近似于正五边形的部分实际被重复计算了。 它的面积的计算是这样实现的,也用到了Green定理! 应用的实例 求积仪(planimeter)
仪器原理 即格林定理,介绍性材料(Oliver Knill, 12/9/2000) The planimeter is a mechanical device for measuring areas in the plane. It has the shape of a ruler with two legs. One leg of length 1 connects the fixed origin (0,0) to (a,b) . A second leg of length 1 connects (a,b) with the end point (x,y) . The point (x,y) determines (a,b) as the intersection of two unit circles centered at (0,0) and (x,y) . The intersection is unique if the angle between the two planimeter legs is smaller than 180 degrees. The planimeter vector field Let F(x,y)=⟨P(x,y),Q(x,y)⟩ be the Planimeter vector field. It is defined by attaching a unit vector orthogonal to the vector (x−a,y−b) at (x,y) . The wheel rotation is the line integral of F along the boundary of R. Green’s theorem tells that this integral is the double integral of curl(F) over the region R . The planimeter vector field is explicitely given by F(x,y)=(P(x,y),Q(x,y))=(−(y−b(x,y)),(x−a(x,y))). Furthermore, curl(F)=Qx−Py is equal to 2+(−ax−by) which is 2 plus the curl of the vector field G(x,y)=⟨b(x,y),−a(x,y)⟩. A direct verification shows that curl(G)=−1 . The Planimeter lineintegral is therefore the area of the enclosed region. 上面这段原理,前半部分可以看看; 后面讲到向量场的旋量时似乎糊涂了, 这个向量场的旋量实际上绝对值就是 1 , 只需要把两个函数a(x,y),b(x,y)解析形式的两种可能显式表示出来一计算就有了,讲得太罗嗦了. 最早的原理介绍1947年就有了: Bibliography. Green’s theorem is the classic way to explain the planimeter. The explanation of the planimeter through Green’s theorem seems have been given first by G. Ascoli in 1947: Guido Ascoli. Vedute sintetiche sugli strumenti integratori (Italian). Rend. Sem. Mat. Fis. Milano, 18:36, 1947.R.W. Gatterdam. The planimeter as an example of Green’s theorem. American Mathematical Monthly, 88:701-704, 1981.L.I. Lowell. Comments on the polar planimeter. American Mathematical Monthly, 61:467-469, 1954.更新已完成 |
【本文地址】
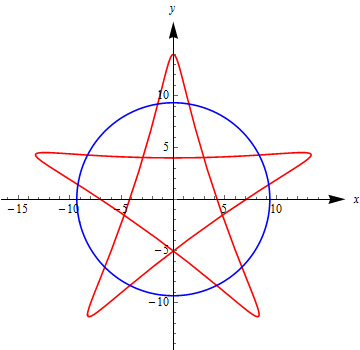
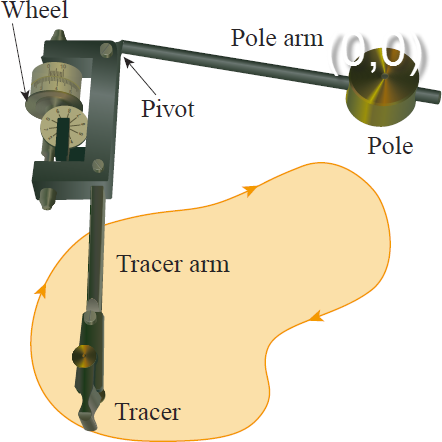 (James Stewart, Calculus, 7th Ed. p1111)
(James Stewart, Calculus, 7th Ed. p1111) 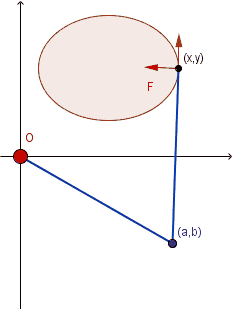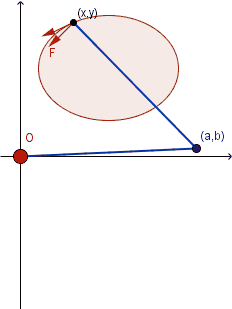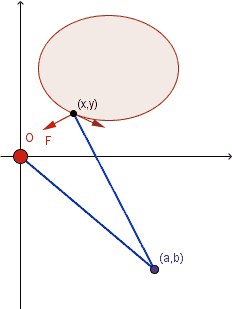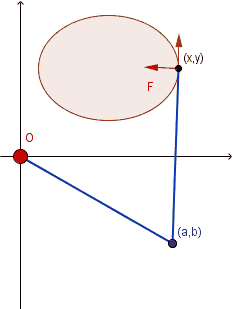 用于计算不规则图形区域的面积, 比如生物学里测量植物叶片的面积或鸟类翅膀的面积, 医学上器官或肿瘤切面面积, 以及地图学或遥感林业研究中地图或遥感影像图上特定地理区域的面积.(数字化时代可能已经有更简单快捷的替代方法)
用于计算不规则图形区域的面积, 比如生物学里测量植物叶片的面积或鸟类翅膀的面积, 医学上器官或肿瘤切面面积, 以及地图学或遥感林业研究中地图或遥感影像图上特定地理区域的面积.(数字化时代可能已经有更简单快捷的替代方法)