Copula系列（一）

当边缘分布（marginal probability distribution）不同的随机变量（random variable），互相之间并不独立的时候，此时对于联合分布的建模会变得十分困难。此时，在已知多个已知边缘分布的随机变量下，Copula函数则是一个非常好的工具来对其相关性进行建模。

copula这个单词来自于拉丁语，意思是“连接”。最早是由Sklar在1959年提出的，即Sklar定理：

以二元为例，若 H(x,y) 是一个具有连续边缘分布的 F(x) 与 G(y) 的二元联合分布函数，那么存在唯一的Copula函数 C ，使得 H(x,y)=C(F(x),G(y)) 。反之，如果 C 是一个copula函数，而 F 和 G 是两个任意的概率分布函数，那么由上式定义的 H 函数一定是一个联合分布函数，且对应的边缘分布刚好就是 F 和 G 。

Sklar认为，对于N个随机变量的联合分布，可以将其分解为这N个变量各自的边缘分布和一个Copula函数，从而将变量的随机性和耦合性分离开来。其中，随机变量各自的随机性由边缘分布进行描述，随机变量之间的耦合特性由Copula函数进行描述。换句话说，一个联合分布关于相关性的性质，完全由其Copula函数决定。

如果已知 H ， F 和 G ，则Copula函数可以表达为：

C(u,v)=H(F^{-1}(u),G^{-1}(v))\\

这里 F^{-1}(u) 代表 F(u) 的反函数，或者叫CDF的逆变换、逆累积分布函数。

假设 X_1,X_2,...,X_N 是 N 个随机变量，它们各自的边缘分布分别为 F_1(x_1), F_2(x_2),...,F_N(x_N) ，它们的联合分布为 H(x_1,x_2,...,x_N) ，则存在一个将边缘分布和联合分布“连接”起来的函数 C(\cdot) ，使得：

H(x_1,x_2,...,x_N)=C(F_1(x_1),F_2(x_2),...,F_N(x_N))\\

而根据边缘分布的CDF的逆变换，即 x_i=F_i^{-1}(u_i)(i=1,2,...,N) ，则可以得到Copula函数的表达形式：

C(u_1,u_2,...,u_N)=H[F^{-1}(u_1),F_2^{-1}(u_2),...,F_N(x_N)]\\

简单解释一下概率积分变换[1]：如果 X_1 和 X_2 都是随机变量（Random Variables，RV），而 U_1 、 U_2 分别是二者的累计概率分布函数，即 U_1=F(X_1)，U_2=F(X_2)

那么：U_1 和 U_2 都服从均匀分布， U_1\sim Uniform(0,1)，U_2\sim Uniform(0,1)

简要的数学证明如下：

F_u(u)=P(U\le u)=P(F(x)\le u)=P(F^{-1}(F(x))\le F^{-1}(u))\\=P(x\le F^{-1}(u))=F(F^{-1}(u))=u

换句话说，任何边际分布的CDF值都均匀分布在区间[0,1]上。如果从任意分布中随机抽取，那么抽取该分布的最大值(U=1)的概率与抽取可能的最小值(U=0)或中值(U= 5)的概率相同。而copula实际上是它所建模的随机变量的CDFs的联合分布。

首先我们可以生成均匀分布的随机变量 x ：

下面，我们想要转化这些样本使他们变成正态分布。那么，我们只需要以 x为CDF值，对正态分布求逆即可，即 F(x_{trans})=x,F^{-1}(x)=x_{trans} 。scipy库中有ppf方法可以满足需求。

如果我们将 x 和 x_{trans} 的分布画在一张图中，就可以直观的看出逆CDF函数的样子。

同理，我们也可以基于 Beta 分布或者 Gumbel 分布来得到类似的图像，这种概率积分变换的本质是相同的。

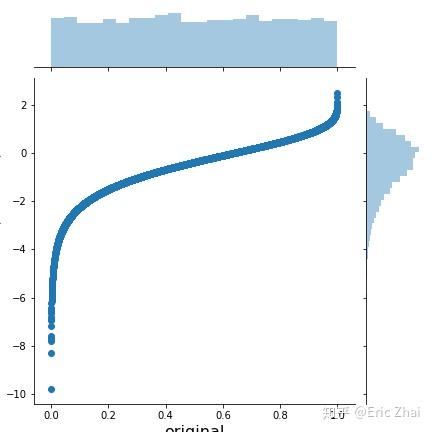而我们如果想要从一个任意的分布到均匀分布(0,1)，那么我们只需要进行一次CDF就可以了。这里我将 x_{trans} 再做一次转化，即：

copula函数非常多，以二元为例，只需要满足下面3个条件的函数即为Copula函数：

1、定义域为 [0,1]\times[0,1] ，值域为 [0,1] ，即 C:[0,1]\times[0,1]\rightarrow[0,1]

2、 C[u,0]=C(0,v)=0,C(u,1)=C(1,u)=u,C(v,1)=C(1,v)=v

3、 0\le \frac{\partial C(u,v)}{\partial u}\le1,0\le \frac{\partial C(u,v)}{\partial v}\le1 ，或 C(u_{2},v_{2})-C(u_{2},v_{1})-C(u_{1},v_{2})+C(u_{1},v_{1})\geq 0 ，对于任意的 0\leq u_{1}\leq u_{2}\leq 1和0\leq v_{1}\leq v_{2}\leq 1

在研究中使用最多的 Copula 函数主要有阿基米德 Copula 函数簇和椭圆 Copula 函数簇(Nelsen 1999[4])两大类。

椭圆 Copula 函数簇有t Copula函数 、Gaussian Copula函数等，两者均有对称的尾部相关性，在中心区域差别不大，差别主要体现在尾部的厚度。

这类copula函数，同时通过已知的多元分布来计算出来的。最为人所知的就是多元正态分布的copula，即高斯copula。

Gaussian copula：高斯copula是a distribution over the unit cube [0,1]^{d} 。它是从多元正态分布 R^d 通过概率积分变换得到的。

对于一个给定的协方差矩阵（correlation matrix） R\in [-1,1]^{d\times d} ，基于参数矩阵R的高斯Copula可以表达成：

C_{R}^{\text{Gauss}}(u)=\Phi _{R}\left(\Phi ^{-1}(u_{1}),\dots ,\Phi ^{-1}(u_{d})\right)\\

其中， \Phi ^{-1} 是标准正态分布的逆累积分布函数， \Phi _{R} 为多元正态分布的联合累积分布函数，它的均值向量为0.，协方差矩阵为 R 。

阿基米德 Copula 函数簇的分布函数定义首先由Genest和Mackay在1986年给出，这一类函数有着统一的函数表达形式：

C(u_1,u_2,...,u_N)=\varphi^{-1}(\varphi(u_1)+\varphi(u_2)+...+\varphi(u_N))\\

如果用wiki加上参数的表示法，则为[4]：

C(u_1,u_2,...,u_N;\theta)=\varphi^{-1}(\varphi(u_1;\theta)+\varphi(u_2;\theta)+...+\varphi(u_N;\theta))\\

其中，函数 \varphi(\cdot) 称为阿基米德Copula函数的生成元（或者叫生成函数，generator function），生成元需要满足：

条件1： \varphi:[0,1]\times\Theta\rightarrow[0,\infty) 是一个连续，严格减函数和凸函数，且 \varphi(1)=0 （ \varphi(1;\theta)=0 ）。

条件2： \varphi^{-1}(t;\theta)=\begin{cases}\varphi^{-1}(t;\theta) \ \text{if} \ 0\le t \le \varphi(0;\theta) \\ 0 \quad \ \qquad \text{if} \ \varphi(0;\theta)\le t \le \infty\end{cases} ，并且要求 \varphi^{-1} 在 [0,\infty) 是N维单调的，即：

(-1)^k\varphi^{-1,(k)}(t;\theta)\ge 0 ，对任意的 0\le t \le 1 ， k=0,1,...,d-2 成立且 (-1)^{d-2}\varphi^{-1,(d-2)}(t;\theta) 是一个非增凸函数。

条件2，对于二元来说，即需要满足对任意的 0\le t \le 1 ，有 \varphi^{-1,'}(t)0

根据不同的生成元函数能够得到不同的阿基米德Copula函数，常见有：Frank Copula、Clayton Copula 及 Gumbel Copula。Gumbel Copula函数对上尾部的厚尾特性比较敏感，对下尾部的厚尾特性不敏感，因此适合于对上尾部厚尾特性明显而下尾部厚尾特性不明显的耦合结构建模；Clayton Copula 函数适合于对下尾部厚尾特性明显而上尾部厚尾特性不明显的耦合结构建模；FrankCopula 的密度分布呈“U”字形，适合于描述具有对称厚尾结构变量的耦合关系。

以上五种Copula 函数的二元分布函数表达式，二元copula函数和生成元如下：

更多阿基米德函数Copula函数，可以参考Nelsen，An introduction to copulas一书中Table 4.1。

数学讲太多了让人烦躁。我们构建一个简单的例子，来看如何利用概率积分变换来认识高斯copula。首先从二元正态分布中生成样本：

通过给 X_1 ， X_2 的CDF进行采样，我们可以将其转化成均匀分布。

现在，我们在上面的基础上（构建的高斯Copula函数），把边缘分布换成Beta分布和Gumbel分布：

那如果没有二者的耦合关系，这个图是怎样的呢？

两张图对比一下，还是很容易看出区别的吧！这就是我们使用copula函数内在的方法了，其核心还是通过均匀分布。

Copula函数主要应用在哪里呢？

该工具最初是用在金融衍生品领域，该函数建模作为衍生品风险度量的工作进行使用。在2008年金融危机中，这个工具被人广发的提及，认为当时采用的高斯copula没有能够完整度量衍生品连带之间的风险，从而导致一系列的违约，进而引发次贷危机、经济危机。

也有人事后写了“‘The Formula That Killed Wall Street’: The Gaussian Copula and Modelling Practices in Investment Banking”（杀死华尔街的公式：高斯copula和在投行的建模应用）的文章来介绍这个工具和现实社会经济的关系，包括很有名的电影《大空头》（The big short），也有这段的描写。

不过我觉得，这种工具显然是能够看到其建模的缺陷之处，把引发金融危机的原因归结为一个工具显然是一个甩锅行为啦，危机绝大多数还是人为。

说回工具本身，除了金融领域，现在很多研究概率分布的领域都在使用copula，例如电力系统领域研究风电、光伏等间歇性能源，也在使用这种方法进行建模。

[1] 本文使用代码

[2] Nelsen RB. An introduction to copulas. 书籍PDF

链接：https://pan.baidu.com/s/1JWfKDunz5gfptHdbaf1Zfg 提取码：usdb

[1] https://waterprogramming.wordpress.com/2017/11/11/an-introduction-to-copulas/

[2] https://twiecki.io/blog/2018/05/03/copulas/

[3] 请用通俗易懂的语言解释一下 Copula 函数，以及其在金融风险管理中的应用？ - jubik的回答 - 知乎 https://www.zhihu.com/question/20123556/answer/154856003

[4] https://en.wikipedia.org/wiki/Copula_(probability_theory)

[5] Nelsen RB. An introduction to copulas. Springer Science & Business Media; 2007 Jun 10.