| 机器学习算法(三):基于horse | 您所在的位置:网站首页 › knn和k近邻的区别 › 机器学习算法(三):基于horse |
机器学习算法(三):基于horse
|
机器学习算法(三):基于horse-colic数据的KNN近邻(k-nearest neighbors)预测分类
项目链接参考:https://www.heywhale.com/home/column/64141d6b1c8c8b518ba97dcc 1 KNN的介绍和应用 1.1 KNN的介绍kNN(k-nearest neighbors),中文翻译K近邻。我们常常听到一个故事:如果要了解一个人的经济水平,只需要知道他最好的5个朋友的经济能力, 对他的这五个人的经济水平求平均就是这个人的经济水平。这句话里面就包含着kNN的算法思想。 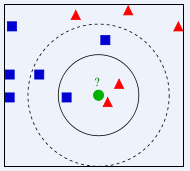
示例 :如上图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。 1) KNN建立过程 1 给定测试样本,计算它与训练集中的每一个样本的距离。 2 找出距离近期的K个训练样本。作为测试样本的近邻。 3 依据这K个近邻归属的类别来确定样本的类别。2) 类别的判定 ①投票决定,少数服从多数。取类别最多的为测试样本类别。 ②加权投票法,依据计算得出距离的远近,对近邻的投票进行加权,距离越近则权重越大,设定权重为距离平方的倒数。 1.2 KNN的应用KNN虽然很简单,但是人们常说"大道至简",一句"物以类聚,人以群分"就能揭开其面纱,看似简单的KNN即能做分类又能做回归, 还能用来做数据预处理的缺失值填充。由于KNN模型具有很好的解释性,一般情况下对于简单的机器学习问题,我们可以使用KNN作为 Baseline,对于每一个预测结果,我们可以很好的进行解释。推荐系统的中,也有着KNN的影子。例如文章推荐系统中, 对于一个用户A,我们可以把和A最相近的k个用户,浏览过的文章推送给A。 机器学习领域中,数据往往很重要,有句话叫做:“数据决定任务的上限, 模型的目标是无限接近这个上限”。 可以看到好的数据非常重要,但是由于各种原因,我们得到的数据是有缺失的,如果我们能够很好的填充这些缺失值, 就能够得到更好的数据,以至于训练出来更鲁棒的模型。接下来我们就来看看KNN如果做分类,怎么做回归以及怎么填充空值。 2 实验室手册 2.1 实验环境 1. python3.7 2. numpy >= '1.16.4' 3. sklearn >= '0.23.1' 2.2 学习目标 了解KNN怎么做分类问题 了解KNN如何做回归 了解KNN怎么做空值填充, 如何使用knn构建带有空值的pipeline 2.3 代码流程二维数据集–knn分类 Step1: 库函数导入 Step2: 数据导入 Step3: 模型训练&可视化 Step4: 原理简析莺尾花数据集–kNN分类 Step1: 库函数导入 Step2: 数据导入&分析 Step3: 模型训练 Step4: 模型预测&可视化模拟数据集–kNN回归 Step1: 库函数导入 Step2: 数据导入&分析 Step3: 模型训练&可视化马绞痛数据–kNN数据预处理+kNN分类pipeline Step1: 库函数导入 Step2: 数据导入&分析 Step3: KNNImputer空值填充–使用和原理介绍 Step4: KNNImputer空值填充–欧式距离的计算 Step5: 基于pipeline模型预测&可视化 2.4 算法实战 2.4.1 Demo数据集–kNN分类Step1: 库函数导入 import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import ListedColormap from sklearn.neighbors import KNeighborsClassifier from sklearn import datasetsStep2: 数据导入 # 使用莺尾花数据集的前两维数据,便于数据可视化 iris = datasets.load_iris() X = iris.data[:, :2] y = iris.targetStep3: 模型训练&可视化 k_list = [1, 3, 5, 8, 10, 15] h = .02 # 创建不同颜色的画布 cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue']) cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue']) plt.figure(figsize=(15,14)) # 根据不同的k值进行可视化 for ind,k in enumerate(k_list): clf = KNeighborsClassifier(k) clf.fit(X, y) # 画出决策边界 x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) # 根据边界填充颜色 Z = Z.reshape(xx.shape) plt.subplot(321+ind) plt.pcolormesh(xx, yy, Z, cmap=cmap_light) # 数据点可视化到画布 plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20) plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.title("3-Class classification (k = %i)"% k) plt.show()
如果选择较小的K值,就相当于用较小的领域中的训练实例进行预测,例如当k=1的时候,在分界点位置的数据很容易受到局部的影响,图中蓝色的部分中还有部分绿色块,主要是数据太局部敏感。当k=15的时候,不同的数据基本根据颜色分开,当时进行预测的时候,会直接落到对应的区域,模型相对更加鲁棒。 2.4.2 莺尾花数据集–kNN分类Step1: 库函数导入 Step2: 数据导入&分析 import numpy as np # 加载莺尾花数据集 from sklearn import datasets # 导入KNN分类器 from sklearn.neighbors import KNeighborsClassifier from sklearn.model_selection import train_test_split # 导入莺尾花数据集 iris = datasets.load_iris() X = iris.data y = iris.target # 得到训练集合和验证集合, 8: 2 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)Step3: 模型训练 这里我们设置参数k(n_neighbors)=5, 使用欧式距离(metric=minkowski & p=2) # 训练模型 clf = KNeighborsClassifier(n_neighbors=5, p=2, metric="minkowski") clf.fit(X_train, y_train)Step4:模型预测&可视化 # 预测 X_pred = clf.predict(X_test) acc = sum(X_pred == y_test) / X_pred.shape[0] print("预测的准确率ACC: %.3f" % acc)预测的准确率ACC: 0.933 我们用表格来看一下KNN的训练和预测过程。这里用表格进行可视化: 训练数据[表格对应list] feat_1 feat_2 feat_3 feat_4 label 5.1 3.5 1.4 0.2 0 4.9 3. 1.4 0.2 0 4.7 3.2 1.3 0.2 0 4.6 3.1 1.5 0.2 0 6.4 3.2 4.5 1.5 1 6.9 3.1 4.9 1.5 1 5.5 2.3 4. 1.3 1 6.5 2.8 4.6 1.5 1 5.8 2.7 5.1 1.9 2 7.1 3. 5.9 2.1 2 6.3 2.9 5.6 1.8 2 6.5 3. 5.8 2.2 2 knn.fit(X, y)的过程可以简单认为是表格存储 feat_1 feat_2 feat_3 feat_4 label 5.1 3.5 1.4 0.2 0 4.9 3. 1.4 0.2 0 4.7 3.2 1.3 0.2 0 4.6 3.1 1.5 0.2 0 6.4 3.2 4.5 1.5 1 6.9 3.1 4.9 1.5 1 5.5 2.3 4. 1.3 1 6.5 2.8 4.6 1.5 1 5.8 2.7 5.1 1.9 2 7.1 3. 5.9 2.1 2 6.3 2.9 5.6 1.8 2 6.5 3. 5.8 2.2 2 knn.predict(x)预测过程会计算x和所有训练数据的距离 这里我们使用欧式距离进行计算, 预测过程如下x = [ 5. , 3.6 , 1.4 , 0.2 ] y = 0 x = [5. , 3.6, 1.4, 0.2] \\ y=0 x=[5.,3.6,1.4,0.2]y=0 step1: 计算x和所有训练数据的距离 feat_1 feat_2 feat_3 feat_4 距离 label 5.1 3.5 1.4 0.2 0.14142136 0 4.9 3. 1.4 0.2 0.60827625 0 4.7 3.2 1.3 0.2 0.50990195 0 4.6 3.1 1.5 0.2 0.64807407 0 6.4 3.2 4.5 1.5 3.66333182 1 6.9 3.1 4.9 1.5 4.21900462 1 5.5 2.3 4. 1.3 3.14801525 1 6.5 2.8 4.6 1.5 3.84967531 1 5.8 2.7 5.1 1.9 4.24617475 2 7.1 3. 5.9 2.1 5.35070089 2 6.3 2.9 5.6 1.8 4.73075047 2 6.5 3. 5.8 2.2 5.09607692 2step2: 根据距离进行编号排序 距离升序编号 feat_1 feat_2 feat_3 feat_4 距离 label 1 5.1 3.5 1.4 0.2 0.14142136 0 3 4.9 3. 1.4 0.2 0.60827625 0 2 4.7 3.2 1.3 0.2 0.50990195 0 4 4.6 3.1 1.5 0.2 0.64807407 0 6 6.4 3.2 4.5 1.5 3.66333182 1 8 6.9 3.1 4.9 1.5 4.21900462 1 5 5.5 2.3 4. 1.3 3.14801525 1 7 6.5 2.8 4.6 1.5 3.84967531 1 9 5.8 2.7 5.1 1.9 4.24617475 2 12 7.1 3. 5.9 2.1 5.35070089 2 10 6.3 2.9 5.6 1.8 4.73075047 2 11 6.5 3. 5.8 2.2 5.09607692 2step3: 我们设置k=5,选择距离最近的k个样本进行投票 距离升序编号 feat_1 feat_2 feat_3 feat_4 距离 label 1 5.1 3.5 1.4 0.2 0.14142136 0 3 4.9 3. 1.4 0.2 0.60827625 0 2 4.7 3.2 1.3 0.2 0.50990195 0 4 4.6 3.1 1.5 0.2 0.64807407 0 6 6.4 3.2 4.5 1.5 3.66333182 1 8 6.9 3.1 4.9 1.5 4.21900462 1 5 5.5 2.3 4. 1.3 3.14801525 1 7 6.5 2.8 4.6 1.5 3.84967531 1 9 5.8 2.7 5.1 1.9 4.24617475 2 12 7.1 3. 5.9 2.1 5.35070089 2 10 6.3 2.9 5.6 1.8 4.73075047 2 11 6.5 3. 5.8 2.2 5.09607692 2step4: k近邻的label进行投票 nn_labels = [0, 0, 0, 0, 1] --> 得到最后的结果0。 2.4.3 模拟数据集–kNN回归Step1: 库函数导入 #Demo来自sklearn官网 import numpy as np import matplotlib.pyplot as plt from sklearn.neighbors import KNeighborsRegressor np.random.seed(0) # 随机生成40个(0, 1)之前的数,乘以5,再进行升序 X = np.sort(5 * np.random.rand(40, 1), axis=0) # 创建[0, 5]之间的500个数的等差数列, 作为测试数据 T = np.linspace(0, 5, 500)[:, np.newaxis] # 使用sin函数得到y值,并拉伸到一维 y = np.sin(X).ravel() # Add noise to targets[y值增加噪声] y[::5] += 1 * (0.5 - np.random.rand(8))Step3: 模型训练&预测可视化 # ############################################################################# # Fit regression model # 设置多个k近邻进行比较 n_neighbors = [1, 3, 5, 8, 10, 40] # 设置图片大小 plt.figure(figsize=(10,20)) for i, k in enumerate(n_neighbors): # 默认使用加权平均进行计算predictor clf = KNeighborsRegressor(n_neighbors=k, p=2, metric="minkowski") # 训练 clf.fit(X, y) # 预测 y_ = clf.predict(T) plt.subplot(6, 1, i + 1) plt.scatter(X, y, color='red', label='data') plt.plot(T, y_, color='navy', label='prediction') plt.axis('tight') plt.legend() plt.title("KNeighborsRegressor (k = %i)" % (k)) plt.tight_layout() plt.show()
当k=1时,预测的结果只和最近的一个训练样本相关,从预测曲线中可以看出当k很小时候很容易发生过拟合。 当k=40时,预测的结果和最近的40个样本相关,因为我们只有40个样本,此时是所有样本的平均值,此时所有预测值都是均值,很容易发生欠拟合。 一般情况下,使用knn的时候,根据数据规模我们会从[3, 20]之间进行尝试,选择最好的k,例如上图中的[3, 10]相对1和40都是还不错的选择。 2.4.4 马绞痛数据–kNN数据预处理+kNN分类pipeline # 下载需要用到的数据集 !wget https://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/3K/horse-colic.csv # 下载数据集介绍 !wget https://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/3K/horse-colic.namesStep1: 库函数导入 import numpy as np import pandas as pd # kNN分类器 from sklearn.neighbors import KNeighborsClassifier # kNN数据空值填充 from sklearn.impute import KNNImputer # 计算带有空值的欧式距离 from sklearn.metrics.pairwise import nan_euclidean_distances # 交叉验证 from sklearn.model_selection import cross_val_score # KFlod的函数 from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.pipeline import Pipeline import matplotlib.pyplot as plt from sklearn.model_selection import train_test_splitStep2: 数据导入&分析 2,1,530101,38.50,66,28,3,3,?,2,5,4,4,?,?,?,3,5,45.00,8.40,?,?,2,2,11300,00000,00000,2 1,1,534817,39.2,88,20,?,?,4,1,3,4,2,?,?,?,4,2,50,85,2,2,3,2,02208,00000,00000,2 2,1,530334,38.30,40,24,1,1,3,1,3,3,1,?,?,?,1,1,33.00,6.70,?,?,1,2,00000,00000,00000,1 1,9,5290409,39.10,164,84,4,1,6,2,2,4,4,1,2,5.00,3,?,48.00,7.20,3,5.30,2,1,02208,00000,00000,1 2,1,530255,37.30,104,35,?,?,6,2,?,?,?,?,?,?,?,?,74.00,7.40,?,?,2,2,04300,00000,00000,2 ......数据集介绍:horse-colic.names 数据中的’?‘表示空值,如果我们使用KNN分类器,’?'不能数值,不能进行计算,因此我们需要进行数据预处理对空值进行填充。 这里我们使用KNNImputer进行空值填充,KNNImputer填充的原来很简单,计算每个样本最近的k个样本,进行空值填充。 我们先来看下KNNImputer的运行原理: Step3: KNNImputer空值填充–使用和原理介绍 X = [[1, 2, np.nan], [3, 4, 3], [np.nan, 6, 5], [8, 8, 7]] imputer = KNNImputer(n_neighbors=2, metric='nan_euclidean') imputer.fit_transform(X)array([[1. , 2. , 4. ], [3. , 4. , 3. ], [5.5, 6. , 5. ], [8. , 8. , 7. ]]) 带有空值的欧式距离计算公式 nan_euclidean_distances([[np.nan, 6, 5], [3, 4, 3]], [[3, 4, 3], [1, 2, np.nan], [8, 8, 7]])Step4: KNNImputer空值填充–欧式距离的计算 样本[1, 2, np.nan] 最近的2个样本是: [3, 4, 3] [np.nan, 6, 5], 计算距离的时候使用欧式距离,只关注非空样本。 [1, 2, np.nan] 填充之后得到 [1, 2, (3 + 5) / 2] = [1, 2, 4] 正常的欧式距离 x = [ 3 , 4 , 3 ] , y = [ 8 , 8 , 7 ] ( 3 − 8 ) 2 + ( 4 − 8 ) 2 + ( 3 − 7 ) 2 = 33 = 7.55 x = [3, 4, 3], y = [8, 8, 7] \\ \sqrt{(3-8)^2 + (4-8)^2 + (3-7)^2} = \sqrt{33} = 7.55 x=[3,4,3],y=[8,8,7](3−8)2+(4−8)2+(3−7)2 =33 =7.55 带有空值的欧式聚类 x = [ 1 , 2 , n p . n a n ] , y = [ n p . n a n , 6 , 5 ] 3 1 ( 2 − 6 ) 2 = 48 = 6.928 x = [1, 2, np.nan], y = [np.nan, 6, 5] \\ \sqrt{\frac{3}{1}(2-6)^2} = \sqrt{48} = 6.928 x=[1,2,np.nan],y=[np.nan,6,5]13(2−6)2 =48 =6.928 只计算所有非空的值,对所有空加权到非空值的计算上,上例中,我们看到一个有3维,只有第二维全部非空, 将第一维和第三维的计算加到第二维上,所有需要乘以3。 表格中距离度量使用的是带有空值欧式距离计算相似度,使用简单的加权平均进行填充。 带有空值的样本 最相近的样本1 最相近的样本2 填充之后的值 [1, 2, np.nan] [3, 4, 3]; 3.46 [np.nan, 6, 5]; 6.93 [1, 2, 4] [np.nan, 6, 5] [3, 4, 3]; 3.46 [8, 8, 7]; 3.46 [5.5, 6, 5] # load dataset, 将?变成空值 input_file = './horse-colic.csv' df_data = pd.read_csv(input_file, header=None, na_values='?') # 得到训练数据和label, 第23列表示是否发生病变, 1: 表示Yes; 2: 表示No. data = df_data.values ix = [i for i in range(data.shape[1]) if i != 23] X, y = data[:, ix], data[:, 23] # 查看所有特征的缺失值个数和缺失率 for i in range(df_data.shape[1]): n_miss = df_data[[i]].isnull().sum() perc = n_miss / df_data.shape[0] * 100 if n_miss.values[0] > 0: print('>Feat: %d, Missing: %d, Missing ratio: (%.2f%%)' % (i, n_miss, perc)) # 查看总的空值个数 print('KNNImputer before Missing: %d' % sum(np.isnan(X).flatten())) # 定义 knnimputer imputer = KNNImputer() # 填充数据集中的空值 imputer.fit(X) # 转换数据集 Xtrans = imputer.transform(X) # 打印转化后的数据集的空值 print('KNNImputer after Missing: %d' % sum(np.isnan(Xtrans).flatten()))Feat: 0, Missing: 1, Missing ratio: (0.33%) Feat: 3, Missing: 60, Missing ratio: (20.00%) Feat: 4, Missing: 24, Missing ratio: (8.00%) Feat: 5, Missing: 58, Missing ratio: (19.33%) Feat: 6, Missing: 56, Missing ratio: (18.67%) Feat: 7, Missing: 69, Missing ratio: (23.00%) Feat: 8, Missing: 47, Missing ratio: (15.67%) Feat: 9, Missing: 32, Missing ratio: (10.67%) Feat: 10, Missing: 55, Missing ratio: (18.33%) Feat: 11, Missing: 44, Missing ratio: (14.67%) Feat: 12, Missing: 56, Missing ratio: (18.67%) Feat: 13, Missing: 104, Missing ratio: (34.67%) Feat: 14, Missing: 106, Missing ratio: (35.33%) Feat: 15, Missing: 247, Missing ratio: (82.33%) Feat: 16, Missing: 102, Missing ratio: (34.00%) Feat: 17, Missing: 118, Missing ratio: (39.33%) Feat: 18, Missing: 29, Missing ratio: (9.67%) Feat: 19, Missing: 33, Missing ratio: (11.00%) Feat: 20, Missing: 165, Missing ratio: (55.00%) Feat: 21, Missing: 198, Missing ratio: (66.00%) Feat: 22, Missing: 1, Missing ratio: (0.33%) KNNImputer before Missing: 1605 KNNImputer after Missing: 0 Step5: 基于pipeline模型训练&可视化 什么是Pipeline, 我这里直接翻译成数据管道。任何有序的操作有可以看做pipeline,例如工厂流水线,对于机器学习模型来说,这就是数据流水线。 是指数据通过管道中的每一个节点,结果除了之后,继续流向下游。对于我们这个例子,数据是有空值,我们会有一个KNNImputer节点用来填充空值, 之后继续流向下一个kNN分类节点,最后输出模型。  results = list()
strategies = [str(i) for i in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 16, 18, 20, 21]]
for s in strategies:
# create the modeling pipeline
pipe = Pipeline(steps=[('imputer', KNNImputer(n_neighbors=int(s))), ('model', KNeighborsClassifier())])
# 数据多次随机划分取平均得分
scores = []
for k in range(20):
# 得到训练集合和验证集合, 8: 2
X_train, X_test, y_train, y_test = train_test_split(Xtrans, y, test_size=0.2)
pipe.fit(X_train, y_train)
# 验证model
score = pipe.score(X_test, y_test)
scores.append(score)
# 保存results
results.append(np.array(scores))
print('>k: %s, Acc Mean: %.3f, Std: %.3f' % (s, np.mean(scores), np.std(scores)))
# print(results)
# plot model performance for comparison
plt.boxplot(results, labels=strategies, showmeans=True)
plt.show()
>k: 1, Acc Mean: 0.800, Std: 0.031
>k: 2, Acc Mean: 0.821, Std: 0.041
>k: 3, Acc Mean: 0.833, Std: 0.053
>k: 4, Acc Mean: 0.824, Std: 0.037
>k: 5, Acc Mean: 0.802, Std: 0.038
>k: 6, Acc Mean: 0.811, Std: 0.030
>k: 7, Acc Mean: 0.797, Std: 0.056
>k: 8, Acc Mean: 0.819, Std: 0.044
>k: 9, Acc Mean: 0.820, Std: 0.032
>k: 10, Acc Mean: 0.815, Std: 0.046
>k: 15, Acc Mean: 0.818, Std: 0.037
>k: 16, Acc Mean: 0.811, Std: 0.048
>k: 18, Acc Mean: 0.809, Std: 0.043
>k: 20, Acc Mean: 0.810, Std: 0.038
>k: 21, Acc Mean: 0.828, Std: 0.038
results = list()
strategies = [str(i) for i in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 16, 18, 20, 21]]
for s in strategies:
# create the modeling pipeline
pipe = Pipeline(steps=[('imputer', KNNImputer(n_neighbors=int(s))), ('model', KNeighborsClassifier())])
# 数据多次随机划分取平均得分
scores = []
for k in range(20):
# 得到训练集合和验证集合, 8: 2
X_train, X_test, y_train, y_test = train_test_split(Xtrans, y, test_size=0.2)
pipe.fit(X_train, y_train)
# 验证model
score = pipe.score(X_test, y_test)
scores.append(score)
# 保存results
results.append(np.array(scores))
print('>k: %s, Acc Mean: %.3f, Std: %.3f' % (s, np.mean(scores), np.std(scores)))
# print(results)
# plot model performance for comparison
plt.boxplot(results, labels=strategies, showmeans=True)
plt.show()
>k: 1, Acc Mean: 0.800, Std: 0.031
>k: 2, Acc Mean: 0.821, Std: 0.041
>k: 3, Acc Mean: 0.833, Std: 0.053
>k: 4, Acc Mean: 0.824, Std: 0.037
>k: 5, Acc Mean: 0.802, Std: 0.038
>k: 6, Acc Mean: 0.811, Std: 0.030
>k: 7, Acc Mean: 0.797, Std: 0.056
>k: 8, Acc Mean: 0.819, Std: 0.044
>k: 9, Acc Mean: 0.820, Std: 0.032
>k: 10, Acc Mean: 0.815, Std: 0.046
>k: 15, Acc Mean: 0.818, Std: 0.037
>k: 16, Acc Mean: 0.811, Std: 0.048
>k: 18, Acc Mean: 0.809, Std: 0.043
>k: 20, Acc Mean: 0.810, Std: 0.038
>k: 21, Acc Mean: 0.828, Std: 0.038
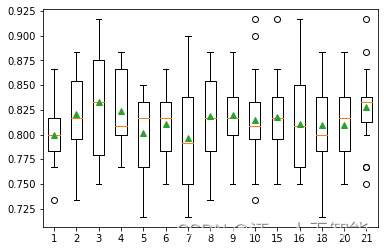
Step 6: 结果分析 我们的实验是每个k值下,随机切分20次数据, 从上述的图片中, 根据k值的增加,我们的测试准确率会有先上升再下降再上升的过程。 [3, 5]之间是一个很好的取值,上文我们提到,k很小的时候会发生过拟合,k很大时候会发生欠拟合,当遇到第一下降节点,此时我们可以 简单认为不在发生过拟合,取当前的k值即可。 2.5 KNN原理介绍k近邻方法是一种惰性学习算法,可以用于回归和分类,它的主要思想是投票机制,对于一个测试实例x, 我们在有标签的训练数据集上找到和最相近的k个数据,用他们的label进行投票,分类问题则进行表决投票,回归问题使用加权平均或者直接平均的方法。knn算法中我们最需要关注两个问题:k值的选择和距离的计算。 kNN中的k是一个超参数,需要我们进行指定,一般情况下这个k和数据有很大关系,都是交叉验证进行选择,但是建议使用交叉验证的时候,k∈[2,20],使用交叉验证得到一个很好的k值。 k值还可以表示我们的模型复杂度,当k值越小意味着模型复杂度表达,更容易过拟合,(用极少树的样例来绝对这个预测的结果,很容易产生偏见,这就是过拟合)。我们有这样一句话,k值越多学习的估计误差越小,但是学习的近似误差就会增大。 距离/相似度的计算: 样本之间的距离的计算,我们一般使用对于一般使用Lp距离进行计算。当p=1时候,称为曼哈顿距离(Manhattan distance),当p=2时候,称为欧氏距离(Euclidean distance),当p=∞时候,称为极大距离(infty distance), 表示各个坐标的距离最大值,另外也包含夹角余弦等方法。 一般采用欧式距离较多,但是文本分类则倾向于使用余弦来计算相似度。 对于两个向量 ( x i , x j ) (x_i,x_j) (xi,xj),一般使用 L p L_p Lp距离进行计算。 假设特征空间 X X X是n维实数向量空间 R n R^n Rn , 其中, x i , x j ∈ X x_i,x_j \in X xi,xj∈X, x i = ( x i ( 1 ) , x i ( 2 ) , … , x i ( n ) ) x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \ldots, x_{i}^{(n)}\right) xi=(xi(1),xi(2),…,xi(n)), x j = ( x j ( 1 ) , x j ( 2 ) , … , x j ( n ) ) x_{j}=\left(x_{j}^{(1)}, x_{j}^{(2)}, \ldots, x_{j}^{(n)}\right) xj=(xj(1),xj(2),…,xj(n)) x i , x j x_i,x_j xi,xj的 L p L_p Lp距离定义为: L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p L_{p}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{p}\right)^{\frac{1}{p}} Lp(xi,xj)=(l=1∑n∣∣∣∣xi(l)−xj(l)∣∣∣∣p)p1 这里的 p ≥ 1 p\geq1 p≥1. 当 p = 2 p=2 p=2时候,称为欧氏距离(Euclidean distance): L 2 ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_{2}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{2}\right)^{\frac{1}{2}} L2(xi,xj)=(l=1∑n∣∣∣∣xi(l)−xj(l)∣∣∣∣2)21 当 p = 1 p=1 p=1时候,称为曼哈顿距离(Manhattan distance): L 1 ( x i , x j ) = ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ L_{1}\left(x_{i}, x_{j}\right)=\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right| L1(xi,xj)=l=1∑n∣∣∣∣xi(l)−xj(l)∣∣∣∣ 当 p = ∞ p=\infty p=∞时候,称为极大距离(infty distance), 表示各个坐标的距离最大值: L p ( x i , x j ) = max l n ∣ x i ( l ) − x j ( l ) ∣ L_{p}\left(x_{i}, x_{j}\right)=\max _{l} n\left|x_{i}^{(l)}-x_{j}^{(l)}\right| Lp(xi,xj)=lmaxn∣∣∣∣xi(l)−xj(l)∣∣∣∣ |
【本文地址】
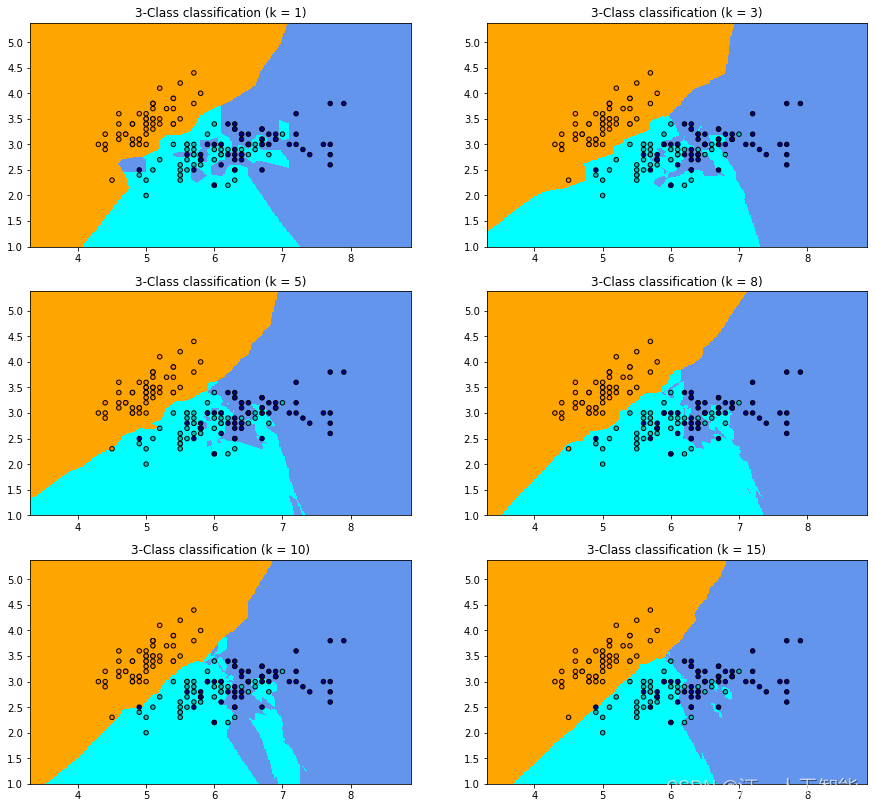 Step4: 原理简析
Step4: 原理简析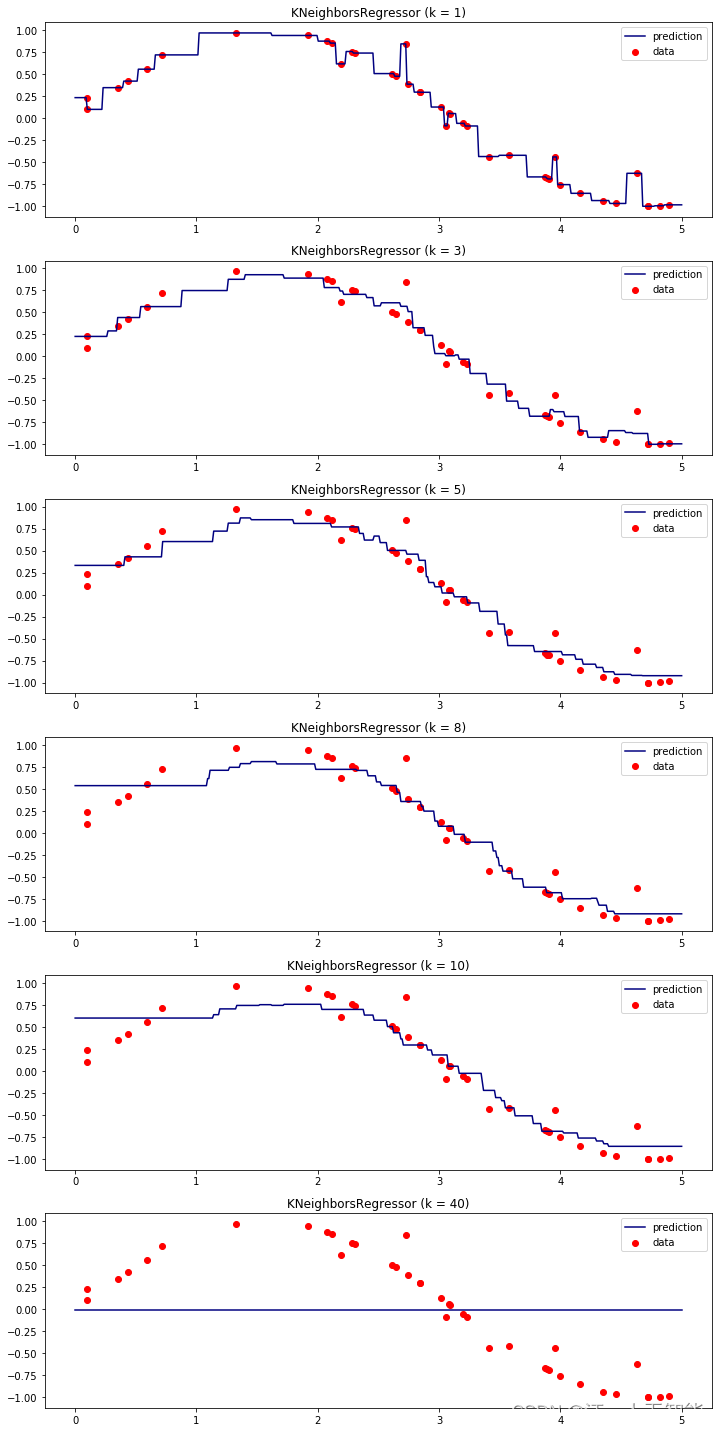 Step4:模型分析
Step4:模型分析