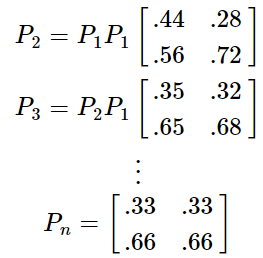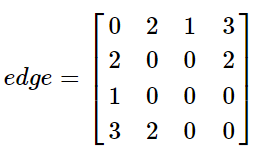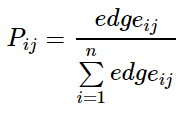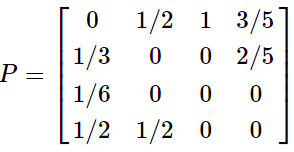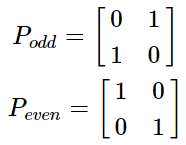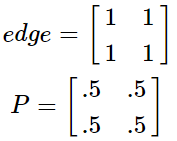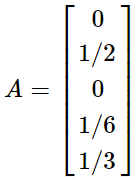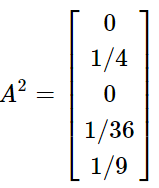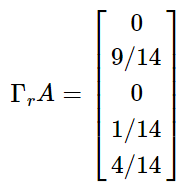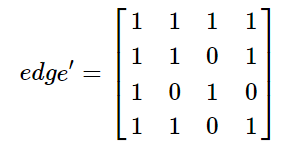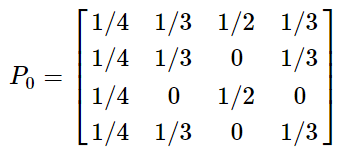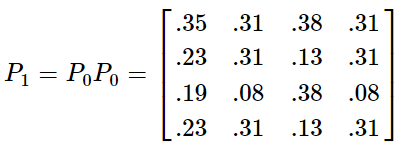马尔可夫聚类 MCL

2024-01-27 18:24| 来源: 网络整理| 查看: 265

本文转载自：聚类算法——MCL 和马尔可夫聚类算法

Background Different Clustering Vector Clustering

我们在描述一个人时，常常会使用他所拥有的特点来表示，比如说：张三，男，高个子，有点壮。那么，这就可以用四维向量来表示，如果再复杂一些，就是更高维的向量空间了。根据各个维度的特征进行聚类是常见的数据分析任务，这类聚类方法包括：系统聚类法、K均值聚类法等。

Graph Clustering

和特征聚类不同，图聚类比较难以观察，整个算法以各点之间的距离作为突破口，可以这样形容：张三，是王五的好朋友，刚认识李四，对赵六很是反感。那么，对于该节点，我们无法直接得出他的特征，但能知道他的活动圈。利用图聚类，可以将同一社交范围的人聚合到一起。马尔科夫聚类MCL就是属于图聚类的一种。

Random Walks

首先看下图：

从图中，我们可以看到，不同的簇，应当具有以下的特点：

位于同一簇的点，其内部的联系应当紧密，而和外部的联系则比较少（惺惺相惜）

也就是说：如果你从一个点出发，到达其中的一个邻近点，那么你在簇内的可能性远大于离开当前簇而到达新簇的可能性——这就是MCL的核心思想。如果在一张图上进行多次的“Random Walks”，那么就有很大可能发现簇群，达到聚类的目的。而“Random Walks”的实现则是通过“Markov Chains”（马尔柯夫链）。

Markov Chains

为了说明 Markov Chain ，我们使用如下的简单例子：

在此图中，我们可以分为两个子图（两簇）： $V(1,2,3,4)$ 和 $V(5,6,7)$ 。在同一簇群中，各点之间完全连接，在不同簇之间，仅有(2,5)一条边。

现在，我们从 $V_1$ 出发，假设每条边都一样，那么则一步之后我们有1/3的概率到达 $V_2$ ，1/3的概率到达 $V_3$ ，1/3的概率到达 $V_4$ ，同时，有0的概率到达 $V_5,V_6,V_7$ 。对于 $V_2$ ，则有1/4的概率到达 $V_1,V_3,V_4,V_5$ ，有0的概率到达 $V_6,V_7$ 。

通过计算每个点到达其余点的概率，我们可以得到如下的概率矩阵：

为了计算简单，我们使用一个更简单的矩阵进行接下来的说明：

这表示的是从任意点出发，经过一步之后到达其它点的概率矩阵，那么，经过两次之后、三次以及最终的概率矩阵为：

关于马尔可夫链，请再具体参考相关资料，此处不作过多赘述。

Weighted Graphs

之前的例子中，图的边是没有权值的，也就是所有的边都是一样的。现在，为每条边添加一个权重（可以理解为亲密程度），那么，就需要重新计算到达每个点的概率了。

假设有如下的图：

那么，其概率矩阵怎么计算？

首先，我们要计算得到邻接矩阵，即：

通过邻接矩阵，我们就可以计算得到概率矩阵了，具体计算公式如下：

最后的概率矩阵如下：

之后的计算相同。

Self Loops

在上述的例子中均未考虑一个重要的问题，我们先来看一个例子：

很简单，就两个点，一条边。那么，它的概率矩阵呢：

仔细观察可以发现，这个概率矩阵不管进行几次计算，都不会收敛，而且，对于P11和P22而言，仅在奇数步后到达，在偶数步时，永远不可达。因此，无法进行随机游走（本来它就没有随机项供人选择）

为了解决这个问题，我们可以为其添加自环来消除奇偶幂次带来的影响：

MCL Markov Chain Cluster Structure

利用 Random Walks 可以求出最终的概率矩阵，但是，在求的过程中，也丢失了大量的信息。

还是这张图，它的概率矩阵和最终的概率矩阵如下：

从最终的矩阵可以看出，其最终概率和起始点的位置无关！对于聚类，这并不是一个好消息，因为我们想要得到的是一个有明显区分度的矩阵来表示不同的类别。因此，我们需要对其进行一定的修改，这也是MCL主要要解决的问题。

Inflation

如果说，前面的内容在介绍 Markov Chain 如何进行 Expansion 的话，那么，现在就添加一个新的过程： Inflation 。这个过程就是为了解决 Expansion 所导致的概率趋同问题的。

简单的说，Inflation 就是将概率矩阵中的每个值进行了一次幂次扩大，这样就能使得强化紧密的点，弱化松散的点。（强者恒强，弱者恒弱）

假设有矩阵 $M^{k\times l}$ ，和一个给定的非负实数 r，经过 Inflation 强化后的矩阵为 $\Gamma _rM$ ，那么它的强化公式如下：

为了更直观的说明，我们来看下面的一个例子：

在 Inflation 之前，向量AA 就是一个正常的概率向量。为了令其具有更明显的区分度，对其进行 Inflation 强化。

假设 r 的取值为2， $A^2$ 如下：

对该向量进行标准化，保证 $\sum_{i=1}^{n}A_i=1$ 。

可以看出，进过一次变换后，区分度进一步的增加，这就为之后的聚类提供了保证。在这里要注明的是Inflation 的参数 r 会影响聚簇的粒度，这个在之后会有说明。

MCL Algorithm

在MCL中， Expansion 和 Inflation 将不断的交替进行，Expansion 使得不同的区域之间的联系加强，而 Inflation 则不断的分化各点之间的联系。经过多次迭代，将渐渐出现聚集现象，以此便达到了聚类的效果。

MCL的算法流程具体如下：

1 输入：一个非全连通图，Expansion 时的参数 e 和 Inflation 的参数 r 。

2 建立邻接矩阵，并添加自环

3 标准化概率矩阵

4 Expansion操作，每次对矩阵进行ee次幂方

5 Inflation操作，每次对矩阵内元素进行r次幂方，再进行标准化

6 重复步骤4和5，直到达到稳定

7 将结果矩阵转化为聚簇

Code

代码实现：

import numpy as np def markovCluster(adjacencyMat, dimension, numIter, power = 2, inflation = 2): columnSum = np.sum(adjacencyMat, axis = 0) probabilityMat = adjacencyMat / columnSum #Expand by taking the e^th power of the matrix. def _expand(probabilityMat, power): expandMat = probabilityMat for i in range(power - 1): expandMat = np.dot(expandMat, probabilityMat) return expandMat expandMat = _expand(probabilityMat, power) #Inflate by taking inflation of the resulting #matrix with parameter inflation. def _inflate(expandMat, inflation): powerMat = expandMat for i in range(inflation - 1): powerMat = powerMat * expandMat inflateColumnSum = np.sum(powerMat, axis = 0) inflateMat = powerMat / inflateColumnSum return inflateMat inflateMat = _inflate(expandMat, inflation) for i in range(numIter): expand = _expand(inflateMat, power) inflateMat = _inflate(expand, inflation) print(inflateMat) if __name__ == "__main__": dimension = 4 numIter = 2 adjacencyMat = np.array([[1, 1, 1, 1], [1, 1, 0, 1], [1, 0, 1, 0], [1, 1, 0, 1]]) markovCluster(adjacencyMat, dimension, numIter) MCL Algorithm Convergence

在作者的论文中，并没有证明MCL算法的收敛性。但是，在实验过程中，总是能够达到最终的收敛状态。下图是一个达到收敛的例子：

为了方便区分不同聚簇，我们将图上的点分为两类：Attractor 和 Vertex 。Attractor 代表了那些有着主导地位的点，这些点吸引着其它的点，将它们牢牢的聚集在周围；Vertex 则表示那些被吸引的点，它们没有主导地位，被 Attractor 所吸引着。其中，Attractor 所在的行必须至少有一个正值，聚集着它所在行中所有正值的点。可以看出，在这个例子中，总共有三个聚簇：{1，6，7，10}，{2，3，5}，{4，8，9，11，12}。

当然，在MCL中也会存在着重叠的聚簇。如下图，当且仅当簇与簇是同构的时才出现一个点被多个聚簇所吸引。