| 二项分布的均值与方差公式的推导 | 您所在的位置：网站首页 › dx与ex的关系公式 › 二项分布的均值与方差公式的推导 |
二项分布的均值与方差公式的推导
|
我们已经知道，若随机变量 X 服从二项分布，即有 X\sim B(n,p) ， 或有 P(X=k)=\mathrm C_{n}^{k}p^k(1-p)^{n-k} ， 式中p为一次试验成功概率，则有 EX=np , DX=np(1-p) 。 关于期望公式的证明可见课本内容，例如下图给出了其推导过程。 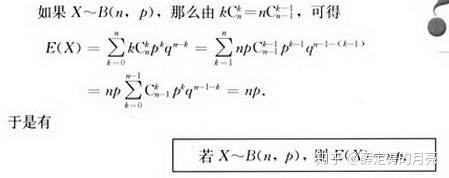 人教版《高中数学2-3》，第62页然而，课本并未给出方差的推导过程，现在此给出： 引理：（1）对于任意随机变量 X ，有DX=EX^2-(EX)^2 ；（2）若有 \xi\sim B(n-1,p) ，则有 E\xi =(n-1)p=\sum_{k=0}^{n-1}{k\mathrm C_{n-1}^{k}p^k(1-p)^{n-1-k}} 。证：（1）由方差DX定义，得 DX=\sum_{i=0}^{n}{P(X=X_{i})(EX-X_{i})^2} ,再由期望EX的定义，将 (X-EX)^2 看做一个随机变量，则有 E(X-EX)^2=\sum_{i=0}^{n}{P(X=X_{i})(EX-X_{i})^2} ,而左边可以写成E(X-EX)^2=E(X^2-2X\cdot EX+(EX)^2)=EX^2-EX\cdot 2EX+(EX)^2=EX^2-(EX)^2，得证；（2）由期望公式可直接得出（详细见上）。故有 DX=EX^2-(EX)^2 =\sum_{k=0}^{n}{k^2\mathrm C_{n}^{k}p^k(1-p)^{n-k}}-(np)^2 =\sum_{k=0}^{n}{k\cdot np\mathrm C_{n-1}^{k-1}p^{k-1}(1-p)^{n-k}}-(np)^2 =np(\sum_{k=1}^{n}{(k-1)\mathrm C_{n-1}^{k-1}p^{k-1}(1-p)^{n-k}+\sum_{k=1}^{n}\mathrm C_{n-1}^{k-1}p^{k-1}(1-p)^{n-k}})-(np)^2 =np(\sum_{k=0}^{n-1}{k\mathrm C_{n-1}^kp^{k}(1-p)^{n-1-k}+\sum_{k=1}^{n}\mathrm C_{n-1}^{k-1}(1-p)^{n-k}p^{k-1}})-(np)^2 =np(E\xi+(p+(1-p))^{n-1})-(np)^2 =np((n-1)p+1)-n^2p^2 =np(1-p) ， 证讫。 |
【本文地址】
公司简介
联系我们