LDL^H分解求逆矩阵与MATLAB仿真(Right

您所在的位置：网站首页 › doolittle分解法例题4阶矩阵 › LDL^H分解求逆矩阵与MATLAB仿真(Right

LDL^H分解求逆矩阵与MATLAB仿真(Right

2024-06-13 20:16| 来源: 网络整理| 查看: 265

通过 $LDL^{H}$ 分解将对称正定厄米特矩阵分解成下三角矩阵L和对角矩阵D来求其逆矩阵

前言

一、LDL^H基本算法

二、LDL^H Right-Looking算法

三、D矩阵求逆

四、L矩阵求逆

五、A矩阵求逆

六、计算量分析

七、MATLAB仿真

八、参考资料

总结

前言

在线性代数中，LDL^H分解是将一个矩阵分解为一个下三角矩阵（L）与一个对角矩阵（D）的过程。由于D是对角矩阵，那么其逆矩阵就等于其所有对角元素的倒数组合成的对角矩阵。求逆矩阵，分解之后便只需要去求L的逆矩阵进而就能求出厄米特矩阵的逆矩阵。

提示：以下是本篇文章正文内容，希望能帮助到各位，转载请附上链接。

一、LDL^H基本算法

对于一个厄米特矩阵A，可以将其写为

$\textbf{A}=\textbf{LDL}^{H}$

其中D为对角矩阵，L为下三角矩阵，且对角元全为1。

A的下三角部分（即 $A_{i,i}\left(j=1,\ldots,N;i\geq j\right)$ ）满足：

$A_{i,j}=\sum_{k=1}^jL_{i,k}D_{k,k}L_{j,k}^*$

$L_{i,i}$ 、 $D_{i,i}$ 可按以下步骤求解：

$L_{1,1}=1,D_{1,1}=A_{1,1};$

$\begin{aligned}L_{i,1}&=L_{i,1}\left/D_{1,1}\right.\left(i=2,\ldots,N\right);\end{aligned}$

c) 对于第 $j\left(j=2,\cdots ,N\right)$ 列：

$L_{j,j}=1,D_{j,j}=A_{j,j}-\sum_{k=1}^{j-1}L_{j,k}D_{k,k}L_{j,k}^*\text{;}$

$\begin{aligned}L_{i,j}&=\frac{A_{i,j}-\sum_{k=1}^{j-1}L_{i,k}D_{k,k}L_{j,k}^*}{D_{j,j}}&\left(j+1\leq i\leq N\right)\end{aligned}.$

d) 如果j=N，则矩阵分解完成；否则j=j+1，返回 c)。

例如，对于4×4阶矩阵，按公式写出每一个元素表达式如下图所示。

二、LDL^H Right-Looking算法

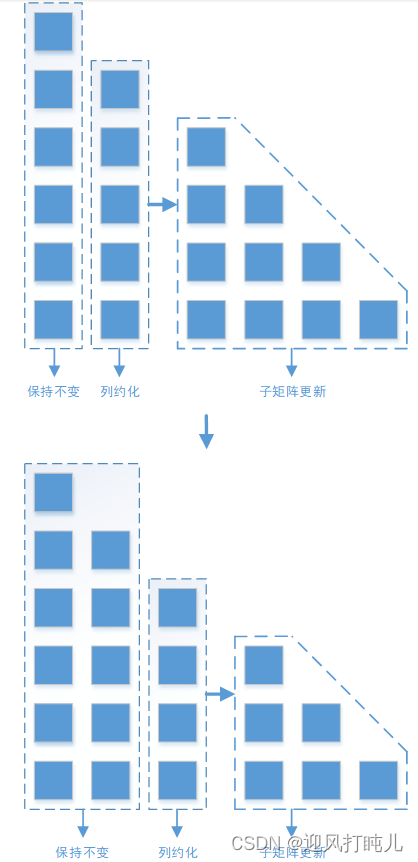
注意到LDL分解的步骤c含有计算 $A_{i,j}-\sum_{k=1}^{j-1}L_{i,k}D_{k,k}L_{j,k}^*$ 部分，该计算在第 j 列完成列约化操作之后即可对后续子矩阵完成部分更新：

$L_{i,j^{\prime}}=L_{i,j^{\prime}}-L_{i,j}D_{j,j}L_{j^{\prime},j}^{*}\left(j^{\prime}=j+1,\ldots,i\right),$

称为Right-Looking结构。

$L_{i,j}$ 、 $D_{j,j}$ 可按以下步骤求解：

$\textbf{L}=tril(\textbf{A})$ （取A的下三角部分）

b) 对于第 $j\begin{pmatrix}j=1,\ldots,N\end{pmatrix}$ 列：

$D_{j,j}=L_{j,j},L_{j,j}=1\text{;}$

c) 对于第 $i\begin{pmatrix}i=j+1,\ldots,N\end{pmatrix}$ 行：

1）执行执行列约化：

$L_{i,j}=L_{i,j}/D_{j,j}\text{;}$

2）更新子矩阵对应行：

$L_{i,j^{\prime}}=L_{i,j^{\prime}}-L_{i,j}D_{j,j}L_{j^{\prime},j}^*\left(j^{\prime}=j+1,\ldots,i\right);$

d）如果 j = N ,则矩阵分解完成；否则j = j+1，返回b）。

例如，对于4×4阶矩阵，按公式写出每一个元素表达式如下图所示。

三、D矩阵求逆

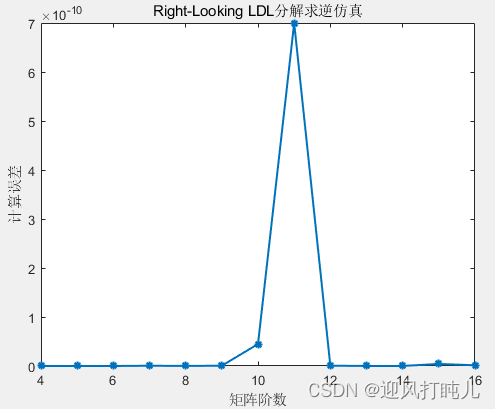
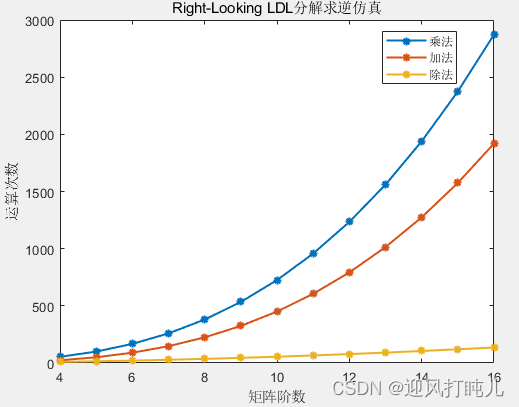
由于D是一个对角矩阵，所以D矩阵的逆矩阵可表示为：

$\textbf{D}^{-1}=\begin{bmatrix} \frac{1}{D_{1,1}} & & & \\ &\frac{1}{D_{2,2}} & & \\ & & \ddots & \\ & & & \frac{1}{D_{N,N}} \end{bmatrix}$

四、L矩阵求逆

由于L是一个下三角矩阵，我们可以对其求共轭转置得到一个上三角矩阵，这样便可以参考下面这篇文章求其逆矩阵：

一种基于约化因子上三角矩阵求逆方法与MATLAB仿真-CSDN博客

五、A矩阵求逆

因为A=LDL^H，所以

$\mathbf{A}^{-1}=(\mathbf{L}^H)^{-1}\mathbf{D}^{-1}\mathbf{L}^{-1}$

六、计算量分析

对于一个N×N阶厄密对称正定A矩阵，

第n $(n=1,\cdots ,N)$ 次列约化需要的除法次数为N-n；

第n次子矩阵更新需要的乘法次数为：

$(N-n+1)(N-n)$

加法次数（减可看成加）为：

$\frac{(N-n+1)(N-n)}2$

那么执行完整个LDLH分解需要的

乘法次数为：

$\sum_{n=1}^N\left((N-n+1)(N-n)\right)=\frac{N^3-N}3$

加法次数为：

$\sum_{n=1}^N\frac{(N-n+1)(N-n)}2=\frac{N^3-N}6$

除法次数为：

$\sum_{n=1}^{N}(N-n)=\frac{N^2-N}2$

执行完之后对对角阵D求逆需要N次除法。

参考一种基于约化因子上三角矩阵求逆方法与MATLAB仿真-CSDN博客，对主对角线全为1的三角矩阵L求逆需要的乘法与加法次数均为

$\frac{N^3-3N^2+2N}6$

因为A=LDLH，那么计算 $\mathbf{A}^{-1}=(\mathbf{L}^H)^{-1}\mathbf{D}^{-1}\mathbf{L}^{-1}$ （注意D-1是对角阵，L-1、(LH)-1是三角阵）需要的乘法次数为：

$\frac{N^3+6N^2+5N}6$

加法次数为：

$\frac{N^3-N}6$

所以通过LDL^H分解求解逆矩阵总共需要的运算次数如下：

乘法：

$\frac{N^3-N}3+\frac{N^3-3N^2+2N}6+\frac{N^3+6N^2+5N}6=\frac{4N^3+3N^2+5N}6$

加法：

$\frac{N^3-N}6+\frac{N^3-3N^2+2N}6+\frac{N^3-N}6=\frac{N^3-N^2}2$

除法：

$\frac{N^2-N}2+N=\frac{N^2+N}2$

七、MATLAB仿真

以MATLAB自带求逆函数inv为对比，仿真得出以下结果：

八、参考资料

https://download.csdn.net/download/m0_66360845/89030881https://download.csdn.net/download/m0_66360845/89030881

总结

以上介绍了一种基于LDL^H，进而求解逆矩阵的方法与MATLAB仿真。小伙伴们认真看完此文章必定有所收获。

【本文地址】

公司简介

联系我们