| 路径规划求最短路径 | 您所在的位置:网站首页 › dijkstra算法过程图解表 › 路径规划求最短路径 |
路径规划求最短路径
|
1.最短路径&&Dijkstra算法——引入
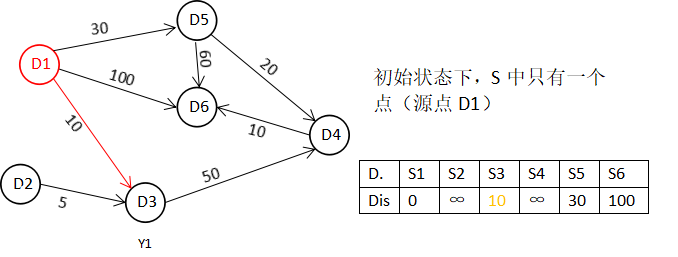
(1)定义:从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径,称为最短路径; (2)算法应用:移动机器人在路径规划中,得知起始点和终止点,在众多的可行驶路径中,选出最短一条(包含各个节点和各个节点间的距离); (3)算法特点:广度优先搜索、赋权有向图(无向图)、单源点(即只存在一个源头点)。 下图是六个顶点和它们边之间的关系。
我们使用二维数组E来存储顶点之间各边的关系,初始值如下: E12345610∞10∞301002∞05∞∞∞3∞∞050∞∞4∞∞∞0∞105∞∞∞200606∞∞∞∞∞0
①E是一个二维数组,E[i][j]表示边(i,j)的e; ②表格里面的数字是两顶点间的实际长度; ③不相邻的两个点之间的距离是无穷大。 2.Dijkstra算法思路(1)Dijkstra算法是典型最短路径算法,用于计算一个节点到其他所有节点的最短路径。以起始点为中心向外层层扩展,直到扩展到终点为止; (2)引入两个集合S(dis数组)和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。 3.Dijkstra算法操作步骤(1)初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。初始时,集合T只有顶点s; (2)然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到集合S中,OK,此时完成一个顶点; (3)再然后,我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值; (4)从dis中找出最小值,重复上述动作,直到S中包含了图的所有顶点。 4.Dijkstra算法示例演示以上图Y1为例,来对迪杰斯特拉进行算法演示(以顶点D1为起点)。
分析:通过数组 dis 可知当前离D1顶点最近是 D3顶点。当选择了 2 号顶点后,dis[2](下标从0开始)的值就已经从“估计值”变为了“确定值”,即 D1顶点到 D3顶点的最短路程就是当前 dis[2]值。将D3加入到T中。
分析:根据现实情况我们知道有新的顶点D3进入集合,发现D3为弧尾的有: < D3,D4 >,那么我们看看路径:D1–D3–D4的长度是否比D1–D4短,其实这个已经是很明显的了,因为dis[3]代表的就是D1–D4的长度为无穷大,而D1–D3–D4的长度为:10+50=60,所以更新dis[3]的值。
分析:我们从除dis[2]和dis[0]外的其他值中寻找最小值,发现dis[4]的值最小,通过之前是解释的原理,可以知道D1到D5的最短距离就是dis[4]的值,然后,我们把D5加入到集合T中,然后,考虑D5的出度是否会影响我们的数组dis的值,D5有两条出度:< D5,D4>和 < D5,D6>,然后我们发现:D1–D5–D4的长度为:50,而dis[3]的值为60,所以我们要更新dis[3]的值.另外,D1-D5-D6的长度为:90,而dis[5]为100,所以我们需要更新dis[5]的值。
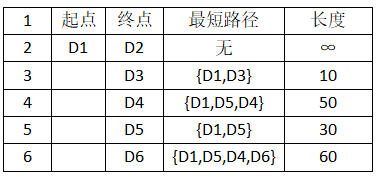
分析:继续从dis中选择未确定的顶点的值中选择一个最小的值,发现dis[3]的值是最小的,所以把D4加入到集合T中。此时集合T={D1,D3,D5,D4},然后,考虑D4的出度是否会影响我们的数组dis的值,D4有一条出度:< D4,D6>,然后我们发现:D1–D5–D4–D6的长度为:60,而dis[5]的值为90,所以我们要更新dis[5]的值。 然后,我们使用同样原理,分别确定了D6和D2的最短路径,最后dis的数组的值如下: D.S1S2S3S4S5S6Dis0∞10503060
因此,从图中,我们可以发现D1-D2的值为:∞,代表没有路径从D1到达D2。最后的结果为
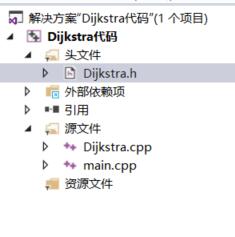
整个项目分为三个部分:Dijkstra.h、Dijkstra.cpp和main.cpp。如下图所示
(1)Dijkstra.h文件的代码 /************************************************************/ /* 程序作者:Willam */ /************************************************************/ #pragma once //保证头文件被编译一次 #include #include using namespace std; /*本程序是使用Dijkstra算法来求解最短路径的问题 采用的邻接矩阵来存储图 */ //记录起点到每个顶点的最短路径的信息 struct Dis { string path; int value; bool visit; Dis() { visit = false; value = 0; path = ""; } }; class Graph_DG { private: int vexnum;//图的顶点个数 int edge;//图的边数 int **arc;//邻接矩阵 Dis *dis;//记录各个顶点最短路径的信息 public: //构造函数 Graph_DG(int vexnum, int edge); //析构函数 ~Graph_DG(); //判断我们每次输入的边的信息是否合法 //顶点从1开始编号 bool check_edge_value(int start, int end, int weight); //创建图 void createGraph(); //打印邻接矩阵 void print(); //求最短路径 void Dijkstra(int begin); //打印最短路径 void print_path(int); };分析: ①头文件的作用是用于程序的各种声明,比如这个头文件,就声明了类class Graph_DG{}和结构体struct Dis{}; ②结构体struct Dis{}:记录起点到每个顶点的最短路径的信息; ③类class Graph_DG{}:里面包含了邻接矩阵信息和相关Dijkstra.cpp文件的5个函数的声明; ④采用的邻接矩阵来存储图。 (2)Dijkstra.cpp文件的代码 #include"Dijkstra.h" //构造函数 Graph_DG::Graph_DG(int vexnum, int edge) { //初始化顶点数和边数 this->vexnum = vexnum; this->edge = edge; //为邻接矩阵开辟空间和赋初值 arc = new int*[this->vexnum]; dis = new Dis[this->vexnum]; for (int i = 0; i < this->vexnum; i++) { arc[i] = new int[this->vexnum]; for (int k = 0; k < this->vexnum; k++) { //邻接矩阵初始化为无穷大 arc[i][k] = INT_MAX; } } } //析构函数 Graph_DG::~Graph_DG() { delete[] dis; for (int i = 0; i < this->vexnum; i++) { delete this->arc[i]; } delete arc; } //判断我们每次输入的边的信息是否合法 //顶点从1开始编号 bool Graph_DG::check_edge_value(int start, int end, int weight) { if (startvexnum || weight < 0) { return false; } return true; } void Graph_DG::createGraph() { cout > start >> end >> weight; //首先判断边的信息是否合法 while (!this->check_edge_value(start, end, weight)) { cout start >> end >> weight; } //对邻接矩阵对应上的点赋值 arc[start - 1][end - 1] = weight; //无向图添加上这行代码 //arc[end - 1][start - 1] = weight; ++count; } } void Graph_DG::print() { cout vexnum) { if (arc[count_row][count_col] == INT_MAX) cout vexnum; i++) { if (!dis[i].visit && dis[i].value |
【本文地址】