| Bezier曲线及其性质 | 您所在的位置:网站首页 › bezier曲线定义 › Bezier曲线及其性质 |
Bezier曲线及其性质
|
本文为Bezier曲线mooc教程学习笔记。 目录 Bezier曲线与曲面[1] Bezier曲线的背景[2] Bezier曲线[3] Bezier曲线详细定义[4] Bezier曲线举例[5] Bernstein 基函数性质[6] 贝塞尔曲线的性质[7] Bezier曲线的生成[8] Bezier曲线的拼接[9] Bezier曲线的升阶与降阶 Bezier曲线与曲面 [1] Bezier曲线的背景
如果要求曲线通过所有的数据点,则属于插值问题; 如果只要求曲线逼近这些数据点,则属于逼近问题。 逼近在计算机图形学中用来设计美观的或符合某些美学标准的曲线。为了解决这个问题,有必要找到一种用小的部分,即曲线段来构建曲线的方法,来满足设计标准。 当用曲线段拟合曲线f(x)时,可以把曲线表示为许多小线段之和,小线段则称为基函数(混合函数) 则曲线可以表示为: 基函数是用于计算和显示的,因此经常选择多项式作为基函数: 1962年,贝塞尔构造了一种以逼近为基础的参数曲线和曲面的设计方法,并用这种想法完成了一种称为UNISURF的曲线和曲面设计系统。想法基点是:在进行外形设计时,**先用折线段勾画出大致轮廓,再用光滑的参数曲线去逼近这个折线多边形。**下图体现折线段与光滑曲线逼近:
折线多边形被成为特征多边形,逼近该多边形的曲线被称为Bezier曲线。 Bezier方法将函数逼近与几何表示结合,使得设计师在计算机上就像使用作图工具一样得心应手,Bezier曲线广泛地应用于很多图形图像软件中,例如Flash、CoralDRAW、Photoshop等。 [2] Bezier曲线Bezier曲线:n次Bezier曲线表示为
系数矢量:系数矢量a_i顺序首尾相接,从a_0的末端到a_n的末端所形成的折线称为控制多边形或贝塞尔多边形。
基函数:贝塞尔给出了基函数的表达式,但并未给出基函数的证明和推导
贝塞尔给出的基函数形式相对复杂,1972年,剑桥大学的博士生Forrest证明了Bezier曲线的基函数可以简化为伯恩斯坦基函数:
针对Bezier曲线,给定空间n+1个点的位置矢量Pi(i=0,1,2,…,n),则n阶Bezier曲线段的参数方程表示如下: 其中,Pi是控制多边形的n+1个顶点,即构成该曲线的特征多边形;B_(i,n)即Bernstein基函数,有如下形式: Pi代表空间的很多点,t在0到1之间,把t带入可以算出一个数,即平面或空间的一个点。随着t值的变化,点也在变化,当t从0变到1时,就得到空间的一个图形,这个图形就是Bezier曲线。
这里可以结合https://www.jianshu.com/p/8f82db9556d2从几何上去理解曲线生成的过程,很直观。 [4] Bezier曲线举例- 一次Bezier曲线
当n=1时,有两个控制点p0和p1,Bezier多项式是一次多项式:
计算基函数:
将基函数带入表达式得到曲线:
恰好为连接起点p0到终点p1的直线段,说明直线段可以用一次贝塞尔曲线来表示。
- 二次贝塞尔曲线 当n=2时,有三个控制点,同理可算得,曲线为:
二次Bezier曲线为抛物线:
- 三次贝塞尔曲线 三次Bezier曲线由四个控制点生成,Bezier多形式是三次多项式:
这四条曲线均为三次曲线,任何三次Bezier曲线都是这四条曲线的线性组合。注意,每个基函数在参数t的整个(0,1)的开区间范围内不为0,这个特点决定Bezier曲线无法对曲线形状进行局部控制,如果改变任一控制点位置,整个曲线的形状都会受影响。 将Bezier三次曲线多项式写成矩阵形式:
正性(非负性):
权性: 基函数有n+1项,n+1个基函数之和恰好为1 端点性质:
对称性: 可以证明,假如保持n次Bezier曲线控制多边形的顶点位置不变,而把次序颠倒过来,这时曲线形状不变但走向相反。 递推性: n次Bernstein基函数可由两个n-1次的Bernstein基函数线性组合而成
导函数:
最大值:
积分
端点性质 顶点P0和Pn分别位于曲线段的起点和终点上,曲线不通过其他控制点,即“逼近”而非“插值”。
一阶导数 Bernstein基函数的一阶导数为
Bezier曲线的一阶导数为
这说明Bezier曲线的起点和终点处的切线方向和特征多边形的第一条边及最后一条线的走向一致:
几何不变性: 指某些几何特性不随坐标变换而变化的特性。Bezier曲线的形状仅与控制多边形各顶点的相对位置有关,而与坐标系的选择无关。 变差缩减性: 若Bezier曲线的特征多边形是一个平面图形,则平面内任意直线与贝赛尔曲线交点的个数不多于该直线与特征多边形的交点个数。
此性质反映了Bezier曲线比其特征多边形的波动更小,即Bezier曲线比特征多边形的折线更光滑。 凸包性: Bezier曲线落在控制点Pi构成的凸包内
生成一条Bezier曲线实际上就是求出曲线上的点,有两种生成曲线的方法。 1. 根据定义直接生成Bezier曲线 绘制Bezier曲线主要有以下步骤:
(1) 首先给出C_n^i的递归计算式:
(2) 将贝塞尔曲线表示为坐标分量的形式:
(3) 根据以上公式则可以直接绘制Bezier曲线 2. Bezier曲线的递推(de Casteljau)算法 根据Bezier曲线的定义确定的参数方程绘制Bezier曲线,因其计算量过大,不太适合在工程上使用。de Casteljau提出的递推算法则要简单得多。
以二次Bezier曲线为例,求出曲线上t=1/3处的点:
那实际上将P0P1和P1P2看做两条一次贝塞尔曲线,二次贝塞尔曲线就是这两个一次贝塞尔曲线的线性组合。**即由(n+1)个控制点定义的n次Bezier曲线可以被定义为分别由前后n个控制点定义的(n-1)次Bezier曲线的线性组合,**由此可以得到Bezier曲线的递推计算公式:
这便是著名的de Casteljau算法,用这一递推公式,在给定参数下,求Bezier曲线上一点P(t)非常有效。该算法稳定可靠,直观简便,可以编出十分简洁的程序,是计算Bezier曲线的基本算法和标准算法。 3. de Casteljau算法几何作图 这一算法可以用简单的几何作图来实现
(1) 依次对原始控制多边形的每一边执行相同的定比分割,所得分点就是由第一级递推生成的中间顶点P_i^1
(2) 对这些中间顶点构成的控制多边形再执行同样的比例分割,得到第二级中间顶点P_i^2
(3) 重复进行下去,直到n级递推得到一个中间顶点P(t),即为所求曲线上的点
拼接Bezier曲线的意义 当控制点为两个点时,Bezier是直线方程;控制点为3个点时,Bezier曲线是二次曲线当控制点很多时,Bezier曲线的次数会很高,在几何设计中,一条Bezier曲线往往难以描述曲线形状,这是由于增加特征多边形的顶点,会引起Bezier曲线次数的提高,而高次多项式又会带来计算上的困难。当次数升高之后,导数零点可能会增加,引起曲线极值点增多,曲线震荡,平滑性下降所以在实际应用中,Bezier曲线都是由一段段低阶Bezier曲线拼接而成,而在拼接的过程中,一定要保证“连续”。即采用分段设计,在连接处保证一定的连续条件。拼接过程 给定两条Bezier曲线P(t)和Q(t),相应控制点为Pi(i=0,1,…,n)和Qi(i=0,1,…,m)
拼接处连续条件 要使他们达到G0连续,则P3=Q0要使他们达到G1连续,则只需要保证P2、P3(Q0)、Q1三点共线 [9] Bezier曲线的升阶与降阶Bezier曲线的升阶 即增加顶点个数,但保证曲线的形状和方向不变,即提高Bezier曲线的次数。 (1) 假设给定原始控制顶点P0~Pn,定义一条n次Bezier曲线
(2) 增加一个顶点后,定义新控制顶点为P0*~Pn*
(3) 形状不变,有
(4) 三次Bezier曲线的升阶实例如下图所示:
可以发现新的控制多边形更加靠近曲线,已证明如果一直升阶,控制多边形将收敛于该曲线。 Bezier降阶 降阶是升阶的逆过程,且无法做到精确相等,只能近似逼近。
|
【本文地址】







![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-r7A46eyz-1597064576321)(/home/neo/.config/Typora/typora-user-images/image-20200810135351773.png)]](https://img-blog.csdnimg.cn/20200810211934907.png#pic_cener)
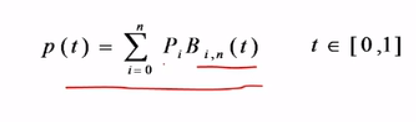
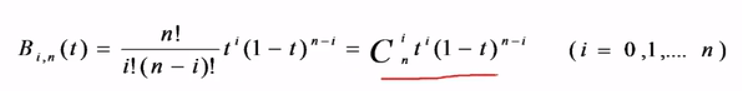








![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JNbbKEk1-1597064576325)(/home/neo/.config/Typora/typora-user-images/image-20200810141936323.png)]](https://img-blog.csdnimg.cn/20200810211426819.png#pic_cnter)



![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lygBGfzH-1597064576327)(/home/neo/.config/Typora/typora-user-images/image-20200810142908894.png)]](https://img-blog.csdnimg.cn/20200810211332412.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L05lbzExMTEx,size_16,color_FFFFFF,t_70#pic_cnter)







![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-itW9eSS5-1597064576328)(/home/neo/.config/Typora/typora-user-images/image-20200810145014030.png)]](https://img-blog.csdnimg.cn/20200810211105946.png#piccenter)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qBpm1PAC-1597064576330)(/home/neo/.config/Typora/typora-user-images/image-20200810151616822.png)]](https://img-blog.csdnimg.cn/20200810211041993.png#pic_cener)


 这里补充一下《计算机图形学》中对Bezier一二阶导的叙述:
这里补充一下《计算机图形学》中对Bezier一二阶导的叙述: 
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oDnQnlQT-1597064576331)(/home/neo/.config/Typora/typora-user-images/image-20200810153548304.png)]](https://img-blog.csdnimg.cn/20200810210928949.png#pic_cnter)

















![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Xfp5jzCE-1597064576333)(/home/neo/.config/Typora/typora-user-images/image-20200810204402629.png)]](https://img-blog.csdnimg.cn/20200810210542690.png#pic_cnter)
