逻辑回归（Logistic Regression)详解

您所在的位置：网站首页 › achievable名词形式 › 逻辑回归（Logistic Regression)详解

逻辑回归（Logistic Regression)详解

2023-08-18 08:24| 来源: 网络整理| 查看: 265

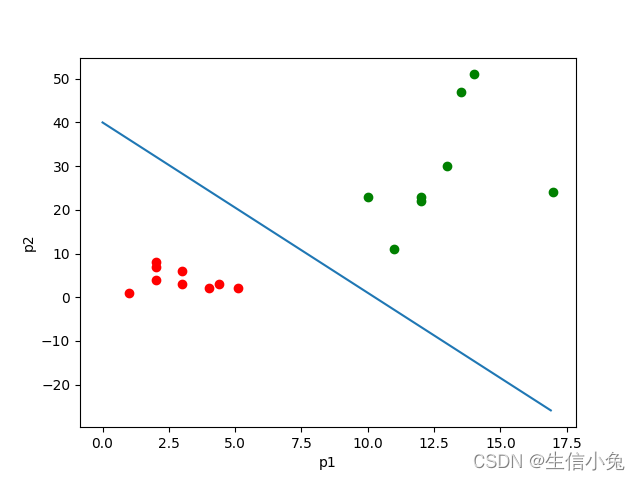
逻辑回归也称作logistic回归分析，是一种广义的线性回归分析模型，属于机器学习中的监督学习。其推导过程与计算方式类似于回归的过程，但实际上主要是用来解决二分类问题（也可以解决多分类问题）。通过给定的n组数据（训练集）来训练模型，并在训练结束后对给定的一组或多组数据（测试集）进行分类。其中每一组数据都是由p 个指标构成。

（1）逻辑回归所处理的数据

逻辑回归是用来进行分类的。例如，我们给出一个人的 [身高，体重] 这两个指标，然后判断这个人是属于”胖“还是”瘦“这一类。对于这个问题，我们可以先测量n个人的身高、体重以及对应的指标”胖“,"瘦”，把胖和瘦分别用0和1来表示，把这n组数据输入模型进行训练。训练之后再把待分类的一个人的身高、体重输入模型中，看这个人是属于“胖”还是“瘦”。

如果数据是有两个指标，可以用平面的点来表示数据，其中一个指标为x轴，另一个为y轴；如果数据有三个指标，可以用空间中的点表示数据；如果是p维的话(p>3)，就是p维空间中的点。

从本质上来说，逻辑回归训练后的模型是平面的一条直线（p=2),或是平面（p=3)，超平面（p>3)。并且这条线或平面把空间中的散点分成两半，属于同一类的数据大多数分布在曲线或平面的同一侧。

如上图所示，其中点的个数是样本个数，两种颜色代表两种指标。这个直线可以看成经这些样本训练后得出的划分样本的直线。那么对于之后的样本的p1与p2的值，就可以根据这条直线来判断它属于哪一类了。

（2）算法原理

首先，我们处理二分类问题。由于分成两类，我们便让其中一类标签为0，另一类为1。我们需要一个函数，对于输入的每一组数据 $x^{(i)}$ ，都能映射成0~1之间的数。并且如果函数值大于0.5，就判定属于1，否则属于0。而且函数中需要待定参数，通过利用样本训练，使得这个参数能够对训练集中的数据有很准确的预测。

这个函数就是sigmoid函数，形式为 $\sigma (x)=\frac{1}{1+e^{-x}}$ 。所以在这里我们可以设函数为

$h(\textup{x}^{i})=\frac{1}{1+e^{-(\textup{w}^{T}\textup{x}^{i}+b)}}$

这里 $x^{i}$ 是测试集第i个数据，是p维列向量 $\begin{pmatrix} x^{i}_{1}&x^{i}_{2}&...&x^{i}_{p}\end{}^{T}$ ；w是p维列向量 $\textbf{w}=\begin{pmatrix}w_{1}&w_{2}&...&w_{p} \end{}^{T}$ ,为待求参数；b是一个数，也是待求参数。

我们发现，对于 $w^{T}x+b$ ,其结果是 $w_{1}x_{1}+w_{2}x_{2}+...+w_{p}x_{p}+b$ 。所以我们可以把

w写成 $\begin{pmatrix}w_{1}&w_{2}&...&w_{p}&b \end{}^{T}$ , $\textbf{x}^{i}$ 写成 $\begin{pmatrix}x_{1}^{i}&x_{2}^{i}&...&x_{p}^{i}&1 \end{}^{T}$ 。 $w^{T}x+b$ 就可以写成 $\textbf{w}^{T}\mathbf{x}$ ,则：

$h(\mathbf{x}^{i})=\frac{1}{1+e^{-\textbf{w}^{T}\textbf{x}^{i}}}$

这样就可以把另一个参数b合并到w中。后面推导也方便很多。当然，我们也可以用用第一种形式来做，本质是相同的。之后就是根据训练样本来求参数w了。

（3）求解参数。

这一部分便是逻辑回归的核心问题了。兔兔在下面将给出两种方法。

（1）极大似然估计。

极大似然估计是数理统计中参数估计的一种重要方法。其思想就是一个事件发生了，那么发生这个事件的概率就是最大的。对于样本i,其类别为 $y_{i}\epsilon (0,1)$ 。对于样本i，可以把 $h(\mathbf{x}_{i})$ 看成是一种概率。yi对应是1时，概率是h(xi)，即xi属于1的可能性;yi对应是0时，概率是1-h(xi)，即xi属于0的可能性。那么它构造极大似然函数

$\prod _{i=1}^{i=k}h(x_{i})\prod _{i=k+1}^{n}(1-h(x_{i}))$ .

其中i从0到k是属于类别1的个数k,i从k+1到n是属于类别0的个数n-k。由于y是标签0或1，所以上面的式子也可以写成：

$\prod _{i=1}^{n} h(\mathbf{x}_{i})^{y_{i}}(1-h(\textbf{x}_{i}))^{1-y_{i}}$

这样无论y是0还是1，其中始终有一项会变成0次方，也就是1，和第一个式子是等价的。

为了方便，我们对式子取对数。因为是求式子的最大值，可以转换成式子乘以负1,之后求最小值。同时对于n个数据，累加后值会很大，之后如果用梯度下降容易导致梯度爆炸。所以可以除以样本总数n。

$L(\textbf{w})=\frac{1}{n}\sum _{i=1}^{n} -y_{i}ln(h(\mathbf{x}_{i}))-(1-y_{i})ln(1-h(\textbf{x}_{i}))$

求最小值方法很多，机器学习中常用梯度下降系列方法。也可以采用牛顿法，或是求导数为零时w的数值等。

（2）损失函数

逻辑回归中常用交叉熵损失函数，交叉熵损失函数和上面极大似然法得到的损失函数是相同的。这里不再赘述。另一种也可以采用平方损失函数(均方误差），即

$J(w)=\frac{1}{n}\sum _{i=1}^{n}\frac{1}{2}(h(x_{i})-y_{i})^{2}$

这个是比较直观的。就是让这个预测函数h(xi)与实际的分类1或0越接近越好。也就是损失函数越小越好。求最小值还是用到上面说到的方法。

目前我们这里已经得到了这两种函数。我们以梯度下降为例，即求损失函数的导数。

对于损失函数（1），导数求解过程如下（需要用到矩阵求导）。

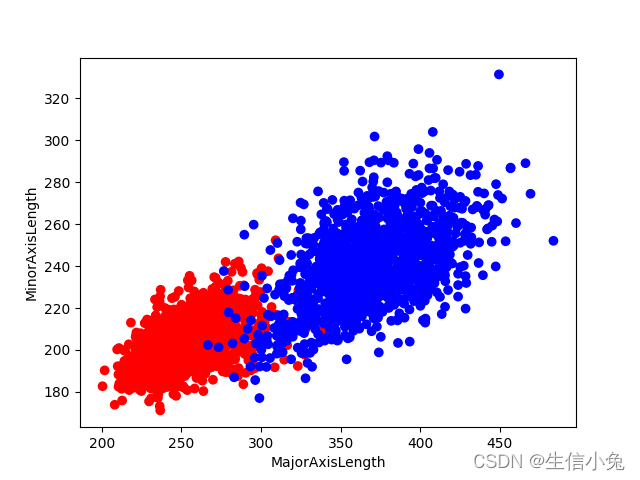
对于损失函数（2），推导过程如下：

（3）算法实现。

兔兔在这里以Dry_Bean_Dataset文件为例。同学们可以在 www.kaggle.com 中下载该数据集，应该比较方便的。

import pandas as pd data=pd.read_csv('Dry_Bean_Dataset.csv') df=pd.DataFrame(data) print(df.columns，df.shape)

我们先看一下数据集的情况，里面有很多个指标，包括菜豆的区域，周长，长轴长、短轴长等。class代表对应菜豆的种类。我们这里为了直观方便（便于在二维平面表示），就选MajorAxisLength,MinorAxisLength这两个指标。由于是二分类，我们就选SEKER和BARBUNYA这两个种类，即前3349组数据。绘制散点图观察。

import pandas as pd import matplotlib.pyplot as plt data=pd.read_csv('Dry_Bean_Dataset.csv') df=pd.DataFrame(data) color=[] for i in df['Class'][0:3349]: if i=='SEKER': color.append('red') else: color.append('blue') plt.scatter(df['MajorAxisLength'][0:3349],df['MinorAxisLength'][0:3349],color=color) plt.xlabel('MajorAxisLength') plt.ylabel('MinorAxisLength') plt.show()

散点图如下：

可见，该数据是可以用一条直线分成两个部分的。

之后，我们需要处理一下数据。把每组数据两个指标及其对应的分类绑在一起（如果用随机梯度下降需要这样处理，批量梯度下降可以不用这样处理），并把每组数据转成列向量。

import numpy as np import pandas as pd data=pd.read_csv('Dry_Bean_Dataset.csv') df=pd.DataFrame(data) label=[] for i in df['Class'][0:3349]: if i=='SEKER': label.append(0) else: label.append(1) x1=df['MajorAxisLength'][0:3349] x2=df['MinorAxisLength'][0:3349] train_data=list(zip(x1,x2,label)) class Logistic_Regression: def __init__(self,traindata,alpha=0.001,circle=1000,batchlength=40): self.traindata=traindata #训练数据集 self.alpha=alpha #学习率 self.circle=circle #学习次数 self.batchlength=batchlength #把3349个数据分成多个部分，每个部分有batchlength个数据 self.w=np.random.normal(size=(3,1)) #随机初始化参数w def data_process(self): '''做随机梯度下降，打乱数据顺序，并把所有数据分成若干个batch''' np.random.shuffle(self.traindata) data=[self.traindata[i:i+self.batchlength] for i in range(0,len(self.traindata),self.batchlength)] return data def train1(self): '''根据损失函数（1）来进行梯度下降，这里采用随机梯度下降''' for i in range(self.circle): batches=self.data_process() print('the {} epoch'.format(i)) #程序运行时显示执行次数 for batch in batches: d_w=np.zeros(shape=(3,1)) #用来累计w导数值 for j in batch: #取batch中每一组数据 x0=np.r_[j[0:2],1] #把数据中指标取出，后面补1 x=np.mat(x0).T #转化成列向量 y=j[2] #标签 dw=(self.sigmoid(self.w.T*x)-y)[0,0]*x d_w+=dw self.w-=self.alpha*d_w/self.batchlength def train2(self): '''用均方损失函数来进行梯度下降求解''' for i in range(self.circle): batches=self.data_process() print('the {} epoch'.format(i)) #程序运行时显示执行次数 for batch in batches: d_w=np.zeros(shape=(3,1)) #用来累计w导数值 for j in batch: #取batch中每一组数据 x0=np.r_[j[0:2],1] #把数据中指标取出，后面补1 x=np.mat(x0).T #转化成列向量 y=j[2] #标签 dw=((self.sigmoid(self.w.T*x)-y)*self.sigmoid(self.w.T*x)*(1-self.sigmoid(self.w.T*x)))[0,0]*x d_w+=dw self.w-=self.alpha*d_w/self.batchlength def sigmoid(self,x): return 1/(1+np.exp(-x)) def predict(self,x): '''测试新数据属于哪一类，x是2维列向量''' s=self.sigmoid(self.w.T*x) if s>=0.5: return 1 elif s

【本文地址】

公司简介

联系我们