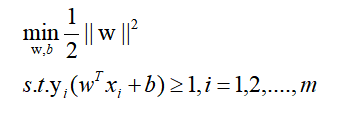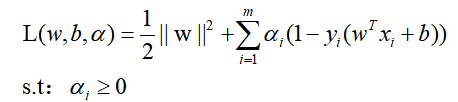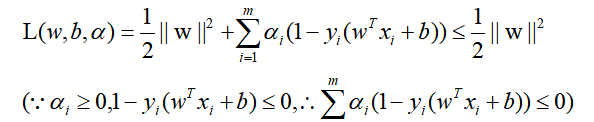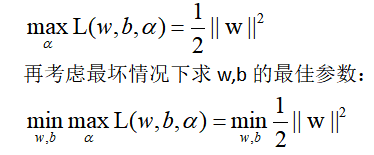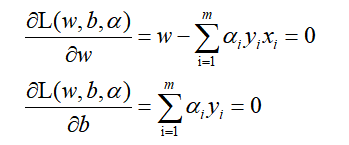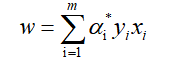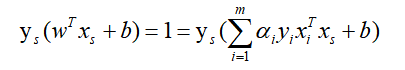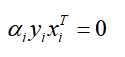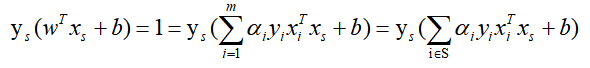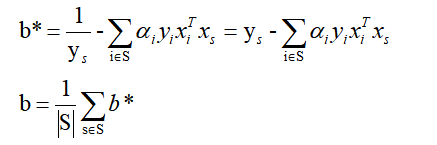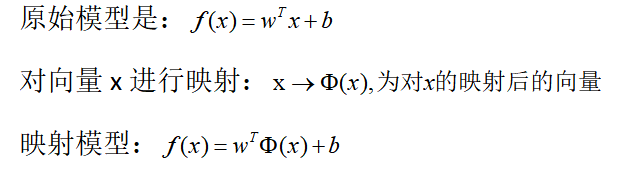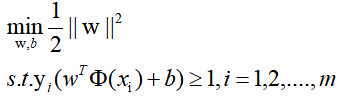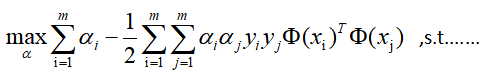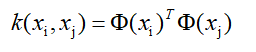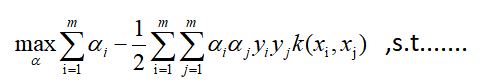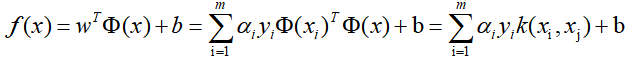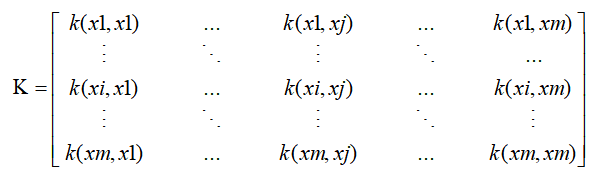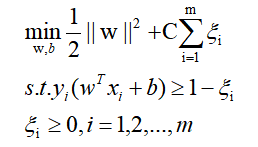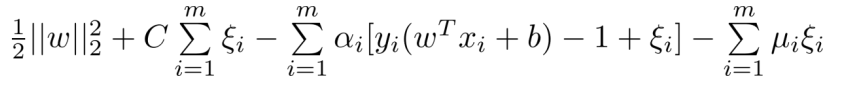ML

目录

 1.导出目标

 2拉格朗日转换

 3对偶问题：

4求对偶问题

5 求b

6 得出模型

6.1 f(x)的约束条件：

7 核函数

7.1 软间隔

7.2 松弛变量：

7.3 KKT约束 

8 SMO求a

8.1对偶问题上，上面已知对偶形式:

8.2.SMO算法思想

8.2.1更新方法

 8.2.2 推导过程

8.2.3选两点a1,a2的方法

8.2.4b和E计算更新

8.3算法伪代码

 8.4完整实现：

python版

9 SVR支持向量回归

10 sklearn实现SVC（支持向量分类）,SVR（支持向量回归）： 

1）分类classification

2）回归Regression

附一个SVC的实现：

因为是希望得出L最小时的一些参数w,b,a，但是目前很难一起求得最佳参数，所以换个思路。因为：

所以能够容易的计算出拉格朗日乘子a约束时的最坏情况是：

 但是m个a的值还是无法求出，而后面会得知，根据L对w,b的求导关系，w,b可以被a表示出来，所以关键变为求a。

根据对偶关系，极大值关系可以转为极小值关系，且转换后的问题会不大于原问题，在取得极值的时候才取等号，也就是：

这样问题变为，先把w,b求导关系代入求L极小值关系，最后再寻找a的问题，最后a的求解会通过SMO等思路求解，具体SMO放到最后讲解，因为太难了。

1）求L的极小值时的w,b，求导：

得出极小值需满足如上这些关系

2）代入L求导关系式，求关于a的极大值：

 所以关键是对这个函数求极大值时的a，假设通过后面的SMO找到了，记为a*，那么显然得到了w的解析式：

因为对于所有支持向量点（正例上支持向量点位于WTx+b = 1超平面上，反例WTx+b= -1）记作(xs,ys)，均有:

根据KKT条件：ai>0时，yi(WTxi+b)-1=0：（必定：WTxi+b = 1 或WTxi+b= -1）即xi必须是支持向量点，而ai=0时:

也就是说对w无影响，因此上式中w还可以简化成只考虑支持向量点计算（实际上这就是SVM称为支持向量机的原因，因为模型真正起作用的，就只是这些支持向量点）：

假设我们有S个支持向量（位于WTx+b = 1，WTx+b= -1超平面上的点集），则对应我们求出S个b∗,理论上这些b∗都可以作为最终的结果， 但是我们一般采用一种更健壮的办法，即求出所有支持向量所对应的b∗，然后将其平均值作为最后的结果：

ai参数求出之后，如上所示，就相当于求出了w,b了。就可以得到模型，进行预测了：

现实中可能有些不存在线性的可分超平面，但是可能映射到更高维度可能就可分了，有证明显示，如果原始空间维度有限，那么一定存在高维特征空间使样本可分。

这样对x的映射关系，可以直接用到上面推导的所有公式里：

原问题映射：

对偶形式映射：

这种映射我们并不知道具体是如何的，因此也不知如何去计算了，所以这里就设想出来核函数的概念了：

 假设出原来的这种内积映射，是等价于某个函数k(.,.)计算的结果。问题就变成了：

求解后模型为：

核函数性质

k是核函数，当且仅当’核矩阵’K总是半正定：

常见核函数列表：

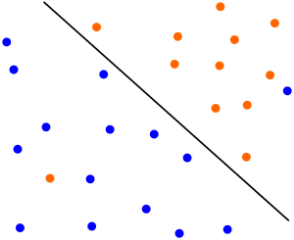
另外核函数线性组合起来还是核函数（系数为正），k1,k1,r1>0,r2>0：k3=r1k1+r2k2 也是核函数

讨论软间隔是因为像这种情况，严格分出来（线性不可分了已经，用核函数可以分）是个弯曲的，但实际上应该就是这下面这样一条斜线才是最好的模型表示：

因此办法是，允许在一些情况下出现错误，引入软间隔的概念，在这个软间隔内允许出错。也就是允许不满足约束：

对于不满足的点，我们会累记一个损失函数，再引入惩罚力度因子C，则可以重新定义优化目标：

显然，这些损失是常数且>=0，因此引入松弛变量的概念替换原来的损害函数计算结果，重写简化：

上式进行拉格朗日变换：为什么这样：https://blog.csdn.net/jiang425776024/article/details/87607526

同样的求导，对偶和上面4一致，省略。最终得到如下对偶问题：

可见，与非软间隔的问题相比，仅仅是对约束ai多了一个上界约束，且约束就是= 1 elif 0 < self.alpha[i] < self.C: #0