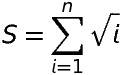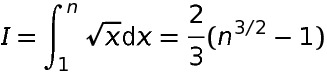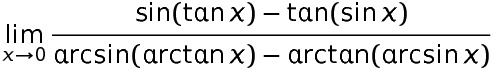邂逅数学

2024-04-09 16:26| 来源: 网络整理| 查看: 265

金庸（1924年3月10日-2018年10月30日）

之所以先讲瑛姑的故事，主要是想缅怀一下最近过世的金庸先生，而瑛姑是《射雕英雄传》中的“神算子”。

在金庸先生的小说中，瑛姑与黄蓉是用几道数学题过招的，我想最令瑛姑刻苦铭心的，当属她自认独创的“九宫格”（3节幻方，俗称洛书）。在以前的两篇文章中，我们插入了两段视频（取自不同的版本），没有看过的读者可以点击链接（注：一篇文章至多允许插播3段视频，我们还是留到后面吧）：

黄蓉（请注意，她老爹是东邪黄药师）临走时给瑛姑出的三道难题（在94版的电视剧中只提了一道，而且是改编之后的第三道，见上述链接）如下：

黄蓉气极，正欲反唇相讥，一转念间，扶着郭靖站起身来，用竹棒在沙地上写了三道算题：

第一道是包括日、月、水、火、木、金、土、罗、计都的"七曜九执天竺笔算"；

第二道是"立方招兵支银给米题"：

第三道是"鬼谷算题"："今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？"

黄蓉气极，正欲反唇相讥，一转念间，扶着郭靖站起身来，用竹棒在沙地上写了三道算题：

第一道是包括日、月、水、火、木、金、土、罗、计都的"七曜九执天竺笔算"；

第二道是"立方招兵支银给米题"：

第三道是"鬼谷算题"："今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？"

其中第三道题最著名，涉及数论中著名的中国剩余定理，我们曾在三篇文章中谈过这个重要结果：

第二道题涉及高阶等差数列的求和，我们也在两篇文中提及：

至于第一题，我们在最近转载的一篇文章也介绍了，见：

◐ 武侠中的数学（四）——七曜九执天竺笔算

相信读者已经看出，鄙人确实是金庸的忠实粉丝。实际上，我几年前就有想法要给金庸先生写封信，问询他老人家何以会想到，在《射雕英雄传》中塑造这样一个“神算子”形象，并借黄蓉之口道出中国古代数学的这些杰出成就，他又是何以了解到中国古代数学这些杰出成就的？后来我将这一想法转告了香港中文大学的陈方正教授，他告诉我，金庸先生身体不好，建议我不要打扰，我就作罢了。

最近我从网上读到一篇文章，对我的问题给出了一个指引，其中有这样一段：

金庸年轻时在《大公报》上写过一篇随笔《圆周率的推算》（后来收进《三剑楼随笔》，全文见本号二条），里面提到一本《算学的故事》：“我在初中读书时，教我数学的是章克标先生，他因写小说出名，为人很是滑稽，同学们经常和他玩闹而不大听他讲书。他曾写过一部《算学的故事》，其中说到有一个欧洲青年花了极长的时间，把圆周率推算到小数点后六百多位。这个圆周率，当然是毫无实用价值的。”

注：章克标（1900-2007）是东京高等师范学校数学系的学生，回国后任教于中学与大学，先教数学，转向文学后又教过语文。有兴趣的读者，可见其自传《世纪挥手》,书名乃金庸手书。

今天我要写的这个题目，一方面是受到饶毅教授的启发，另一方面，其实也是受到金庸先生《天龙八部》里的一段情节（第46节，酒后君问三语，西夏公主提问招亲）的启发，有兴趣的读者可见下述视频，我不再展开（我觉得这本质上是一个对偶的话题：你所提出的最好的问题是什么？）：

西夏公主（毋宁说是金庸前辈）提出三个简单的问题：

让天下群雄尽显各自本色（最令人唏嘘的乔峰的回答，不过在原著中，乔峰是先行离开从而回避了这些问题）。好了，我们打住。我只说，这几个问题问得很好，至于大家的回答，可以在留言区分享。

现在我们来看几位著名人物所分享的刻骨铭心的数学题吧！

杨振宁（1922-）

杨振宁

在本号最近推出的张奠宙教授对杨振宁先生的访谈：

◐ 杨振宁和当代数学

中，杨振宁先生提到了他在西南联大时，陈省身先生给他们出的一个题目：

在西南联大，我很可能旁听过陈省身的好几门数学课，但是根据保存至今的成绩单，我只是在1940年秋季学期正式选修过他讲授的微分几何课程。当时我是物理系的三年级学生。

张：这门课您有所得益吧?

杨：当然。不过我已经记不清楚上课的情形了，只有一件事印象很深：如何证明每一个二维曲面保角等价于平面?我知道如何把度量张量化成

的形式，但是想了很久都想不出怎样使A=B。有一天，陈先生告诉我要用复变量，并写下：

这个式子。学到这简单的妙诀，是我毕生难忘的经历。

张：这门课您有所得益吧?

杨：当然。不过我已经记不清楚上课的情形了，只有一件事印象很深：如何证明每一个二维曲面保角等价于平面?我知道如何把度量张量化成

的形式，但是想了很久都想不出怎样使A=B。有一天，陈先生告诉我要用复变量，并写下：

这个式子。学到这简单的妙诀，是我毕生难忘的经历。

最近我从西北大学刘建新博士的博士论文中得知，原来，这结果和技巧都归功于高斯(Gauss)。这个题目我们不再展开（若有需要，留言区讨论），我想重点在于，杨先生想说，陈先生令他认识到复数的重要性。陈省身先生常说的一句话是，复数使数学简单化（一个最显著的例子是代数基本定理：多项式在复数域内必有零点）。我想下面这本书（一本复分析的研究生教材）的标题很能够表达这个意思：

关于做学问的经验之谈，杨先生写过一篇优美的文章，值得推荐给各位读者：

◐ 杨振宁，我的学习与研究经历，《物理》，2012年

徐利治（1920-）

徐利治

当今之中国，资历最老的数学家恐怕要属徐利治先生了，他1920年出生，很快就要100岁了。我们曾经在本号推送过他的文章

在追忆我的大学老师华罗庚先生一文中，徐利治曾回忆起他与华罗庚先生对初等数论中一个定理之证明的讨论，从中可以看出，学生时代的徐利治前辈头脑之活跃（用今天的话来说，就是“脑洞大开”）。

在湖南教育出版社出版的《徐利治访谈录》（袁向东，郭金海访谈整理）中，他也分享了他在西南联大求学时请教陈省身先生的一道题目（见上书73-74页）：

我在西南联大二年级的时候，有一次到数学系办公室请教陈先生先生一个级数求和问题。这个问题是：

如何计算？

陈先生看了很久，没有回答出来。后来我才知道，这个求和问题没有精确的公式表达，但可以用欧拉-麦克劳林求和公式（Euler–Maclaurin formula）做近似计算。可见，当时陈先生的分析基础也不是十分强。

我在西南联大二年级的时候，有一次到数学系办公室请教陈先生先生一个级数求和问题。这个问题是：

如何计算？

这里徐利治先生分享了他的后见之明：这个和是求不出来的——其结果没有一个简单的公式表达。那么能做的，只是近似求和，即，求出这个和的一个近似值。换言之，我们所能解决的，是下述问题（请注意，这里改变了问题的提法，唯有如此，方才可解）：

问题0：求

的近似值。

徐利治先生建议的方法是用欧拉-麦克劳林求和（留给有兴趣的读者），下面我们介绍一个更简单的方法（取自一本教材Mathematics for Computer Science，是MIT同名课程的教材，可在MIT公开课网站免费下载）。为求出这个近似值，我们需要下述结果（提请读者注意，这里基本的想法是，求和是积分的离散版本，求和与积分互为很好的近似。）：

注：如果你学过微积分，也许会想起正项级数的积分判别法，它依赖于上述定理的另一半，此处从略。

好了，现在我们来解决问题0。

据此定理，为估计求和

只需求出积分

上面将问题重新提出的变通策略，正好印证了大数学家阿贝尔(Abel）的高见：

人们应该力求给问题一种形式，使得它总是可解的，这总是可能的。以恰当选择的形式提出问题，其叙述本身就会包含着解答的种子。

阿贝尔

何兆武（1921-）

何兆武

我还想到西南联大的另一位杰出校友，他叫何兆武，著名的历史学家。在《上学记》（何兆武口述，文靖执笔）一书（90-91页）中，他曾回忆起他参加的1939年的西南联大高考所遇到的一道数学题：

那一年数学考题非常之难，也不知道是谁出的，比我们中学所学的更深。其中有一个题目我还记得，在椭圆上任取一个点，问：把这个点到椭圆上每个点连线的中点连接起来，是什么图形，并列出方程。我知道连起来是一个内切小椭圆，给描出来了，可是列不出公式。有个同学数学学得非常好，考完了以后跟我讲，这道题不能用正坐标（即直角坐标）表述，得用极坐标。经他一说我就想起来了，所以印象特别深。另外，这件事也给了我极大的启发，一个终生受益的启发：当我们的思想解释不通的时候，就得换一个坐标，不能死硬地按原来的模式去套。

我想，历史中真正学术上、思想上的重大突破，大概都需要坐标的转换。有些用原来的坐标解释不了了，却仍在那里生搬硬套，是行不通的。比如，……

The greatest discovery of my generation is that a human being can alter his life by altering his attitudes.【看来不仅学术如此，人生也是如此，也需要换坐标（观点）】

本人尝试了一下，感觉这个问题用直角坐标也很简单。不过，我对何兆武先生最后的领会（换坐标）深有共鸣。我还发现，《大话西游》里头也有个经典的坐标变换（遗憾的是，春三十娘的扮演者蓝洁瑛最近去世了

）：

《大话西游》里有个经典的坐标变换（换衣服），有兴趣的读者，请参见陈省身先生的通俗演讲：大师演讲：从三角形到流形

我们也曾指出，江湖上有些算命术士很会利用坐标，见

◐ 算命是胡扯，猜姓却不然——续篇

顺便说一句，第一节里陈省身先生出给杨振宁的那个题目，其实就是证明曲面上存在等温坐标（一种方便的坐标）。

阿诺德（V. I. Arnold，1937-)

阿诺德

跟俄国的许多数学大师（如柯尔莫果洛夫、盖尔范德）一样，阿诺德(1937-2010)不仅是卓有成就的数学家，也是极优秀的数学教育家。他曾写过一本书：

其中收入了为5-15岁的孩子准备的77个数学问题，从维基百科Vladimir Arnold条目可以搜到这本书的电子版（可免费下载）。有兴趣的读者，也可以参见和乐数学推送的介绍先一睹为快：

20世纪最伟大数学家之一的阿诺德及其为儿童和父母设计思维训练题

阿诺德在1991年的Notices访谈中曾提及儿时一次有趣的数学经历：

很多俄罗斯家庭都有给孩子出诸如此类的各种问题的传统，我的父母也不例外。不过我第一次真正的数学经历是在小学，当时我们的教师I. V. Morozkin向我们提出以下问题：甲乙两个老太太在日出时同时出发，甲从A地往B地走，乙从B地往A地走，都是匀速前进。她们在正午相遇，然后继续不停地走，如果甲到达B地的时间是下午四点，而乙到达A地的时间是下午九点。请问，当天日出的时间是几点？

请允许我将这个题目（收入第5题到Arnold的书中）重新提取成下述形式：

问题1（侠客行）：甲、乙两个侠客约定在某一天上午的某个时间同时出发，甲从 A 地往 B 地走，乙从 B 地往 A 地走，都是马不停蹄匀速前进。他们恰好在当天正午相遇，抱拳问候之后立即挥手告别（侠客行，片刻也不耽误，所谓“君子不下马，各自奔前程”是也），继续不停地走，如果甲达到 B 地的时间是下午 4 点，而乙到达 A 地的时间是下午 9 点。请问，他们约定的出发时间是几时？

阿诺德说：

当时我花了一整天的时间来思考这个老掉牙的问题，而答案则是一种出乎意料的方式得到的。

在高等教育出版社“数学概览”丛书第5号作品《惠更斯与巴罗，牛顿与胡克》一书中，阿诺德提出过一个有趣的问题，也许可以考考各位学过微积分的朋友（下文引自中译本）：

下面这例问题，是像巴罗、牛顿和惠更斯这样一些人在几分钟内就能解决的，而在我看来，当今的数学家（我所知的唯一例外是法尔廷斯）还不能很快就求解出来：

问题2（求极限）：计算

朋友，如果算不出来也没有关系，毕竟你不必胜过法尔廷斯——要知道他可是1986年的菲尔兹奖得主；同时我也实话实说，我没算出来（但我有朋友很快就算出来，并点评说：“这是文中我印象最深的一段，也算是高数老师在计算机时代的最后的尊严。”）。有没有感觉我这个高数老师被打脸了？

没关系哦，我早已习惯了这种常态：

来，我们听个歌放松一下，有请从台湾大学数学系转向歌坛的周华健同学，为大家带来一曲《难念的经》（《天龙八部》主题曲，林夕作词，周华健作曲）

怎么样？心情好多了吧。早跟你说过了：

几个补充的练习

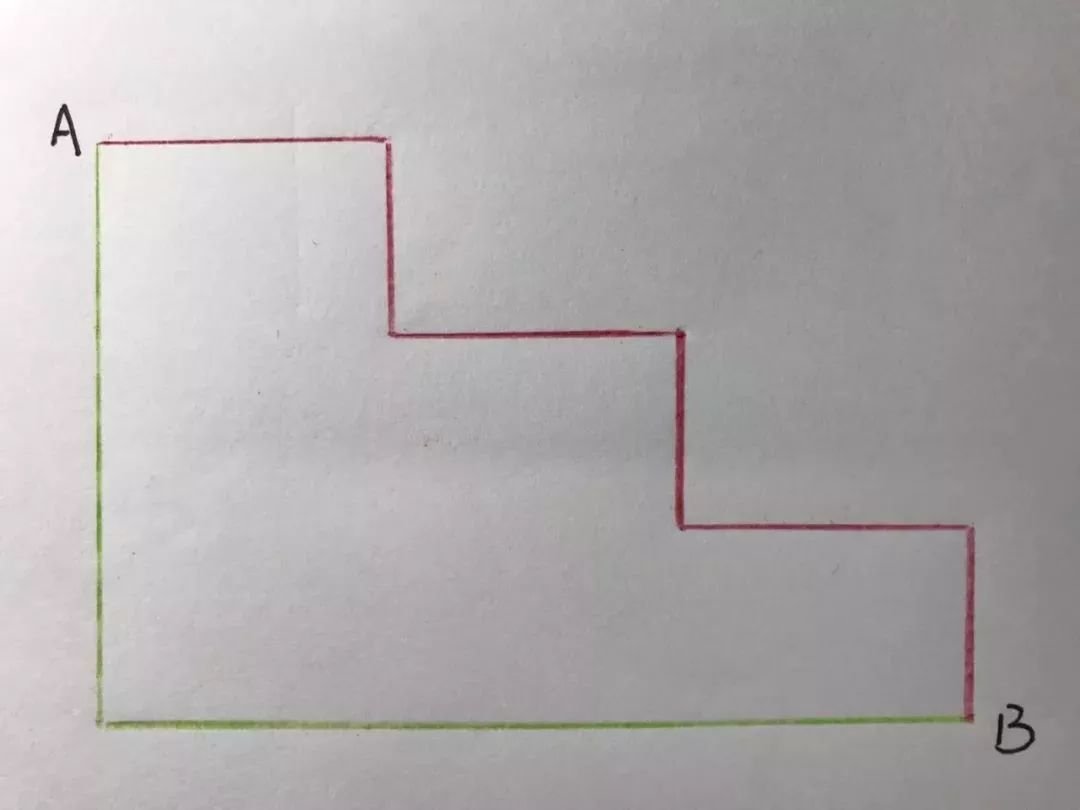
《射雕英雄传》之东邪西毒剧照；注意，这是西毒欧阳锋，而不是东邪黄药师，后者大概是金庸武侠小说中数学最好的（新加坡国立大学数学系的曾衡发教授首先向我提及这一点）。

问题3（小学水平：阿诺德+加州大学伯克利分校数学系伍鸿熙教授提供）：

有一杯红酒和一壶茶水，先从茶水中盛一勺倒入红酒中，均匀搅拌后再盛一勺倒回茶水中。请问此时杯中含有的茶水和壶中含有的红酒，哪个更多？如果没有搅拌均匀，情况又会怎样？

【有兴趣的读者，可以参考伍鸿熙教授《数学家讲解小学数学》第23章“一些有趣的应用题” 问题4，中译本（赵洁、林开亮译，北京大学出版社）第316页】

问题4（小学-初中水平：西北大学数学系刘建新博士提供）：

如图，从A到B有两条路线。绿色路线由一条竖直方向的线段和一条水平方向的线段组成；红色路线是阶梯状的，每段线段分别是水平和竖直的。问两条路线哪个更近？

问题5（初中水平：本人初三经历，曾作为思考题在课堂上出给大一新生）：

在下述矩形中，已知三个角上的三角形的面积分别为3，4，5，求中间的三角形的面积。

问题6（高中水平：西北农林科技大学物理系刘昌勇教授提供，是上世纪30-40年代的一道高考题）：

已知为方程式

的一根，求其余各个根。

已知为方程式

的一根，求其余各个根。

问题7（大学水平：美国加州大学尔湾分校数学系陆志勤教授提供）：

证明：在n维欧氏空间中，两两夹角为钝角的向量至多有 n+1 个.

问题8(小学、初中、高中、大学水平：本人提供，曾作为离散数学作业留给计算机专业大二学生，取自当时我参考的一本教材，Mathematics for Computer Science，是MIT同名课程的教材，可以在MIT公开课网站免费下载）：

Here is a game you can analyze with number theory and always beat me. We start with two distinct, positive integers written on a blackboard. Call them a and b. Now we take turns. (I'll let you decide who goes first. ) On each turn, the player must write a new positive integer on the board that is the difference of two numbers that are already there. If a player cannot play, then s/he lose.

For example, suppose that 12 and 15 are on the board initially. Your first play must be 3, which is 15-12. Then I might play 9, which is 12-3. Then you might play 6, which is 15-9. Then I cant play, so I lose.

(a) Show that every number on the board at the end of the game is a multiple of gcd(a,b). 【注： gcd(a,b) 表示 a, b 的最大公因子】

(b)Show that every positive multiple of gcd(a, b) up to max(a, b) is on the board at the end of the game. 【注： max(a,b) 表示 a, b 中最大的那一个数】

【这道题目英文很简单，我就不翻译了——原谅我这一生放荡不羁爱自由】

(a) Show that every number on the board at the end of the game is a multiple of gcd(a,b). 【注： gcd(a,b) 表示 a, b 的最大公因子】

(b)Show that every positive multiple of gcd(a, b) up to max(a, b) is on the board at the end of the game. 【注： max(a,b) 表示 a, b 中最大的那一个数】

【这道题目英文很简单，我就不翻译了——原谅我这一生放荡不羁爱自由】

问题9（大学水平，本人经历，至今都还不知道怎么做，所以刻骨铭心。借这个机会向大家征解，请方家赐教）：

(Taussky) 在平面上给定n条处于一般位置（这里理解为，任意三条直线都不共点）的直线。证明：在由这些直线构成的C_n^3个三角形的内切圆中，有且仅有一个圆与其余n-3条直线相交或相切。证明，存在一点，它到诸直线的距离不大于任何别的点到这些直线的距离之最大者。【引自《函数构造论引论》，J. 托德著，第29页，问题3.26，Taussky恰好是作者的夫人】

问题10（大学水平，不久前准备一个科普报告时遇到，是剑桥大学本科生荣誉学位考试的题目，我也不会，一并求教方家）：

如图，证明人在深水中平稳游泳时激起的波浪其夹角总是2arcsin(1/3)。