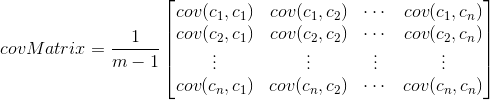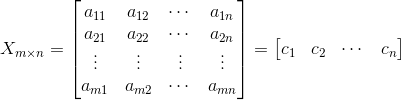
在我们学习概率论的时候，很多时候我们不能深刻理解概率论中的数字特征所具有的含义，本文章尝试去帮助读者理解一些术语、概念。 　　 　　什么是数字特征？要回答这个问题，先得弄清楚什么是特征。特征是一个客体或一组客体特性的抽象结果。特征是用来描述概念的。任一客体或一组客体都具有众多特性，人们根据客体所共有的特性抽象出某一概念，该概念便成为了特征。而数字特征是对于数字的一种抽象方式，不同的抽象方式表现数字不同方面的数字特征（如，均值表现平均水平，方差表示离散程度）。从信息的角度来说，特征化（抽象）是压缩信息的一种方式。

　　为何会有数字特征？特征化是人们压缩数据的一种方式，它能够反映一些群体的某方面的特点。举个简单的例子，校长去某个班调查学生的学习水平，他不太可能去查看询问每个人的成绩（那样子是十分耗时的一件事情）。所以我们将班级的成绩信息进行压缩，压缩成均值，众数，标准差等，以此来为校长提供其所关心的平均水平，成绩差异程度等。

　　在数字特征的构造中，统一量纲 是一个十分重要的原则，下面的各个的数字特征中都会有所体现。下图说明，各个数字特征之间可以进行的运算 图1：（未涉及协方差，相关系数）

一些 同一随机变量的不同数字特征是可比较的。

区分概率论与统计学（参考）： 【知乎】概率论与统计学的关系是什么？

　　要想理解数字特征，弄清楚随机变量这一个概念是十分重要的。

　　本小节主要介绍概率论中常见的一些数字特征，并且说明其直观的物理意义。这里只讨论离散型随机变量的数字特征。

　　在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和。是最基本的数学特征之一。它反映随机变量平均取值的大小。其公式如下：

　　（variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。在许多实际问题中，研究方差即偏离程度有着重要意义。 　　方差( D(X) 或 Var(X) )计算公式如下： 　　

公式逐步解释： [X−E(X)] —> [X−E(X)]2 —> E{[X−E(X)]2}

[X−E(X)] 是计算随机变量中各个值与期望的距离（反映的是以 E(X) 为基准计算的偏差）。但是只是将偏差进行求和，可能导致结果为0的情况（会产生离散程度较高，评价却为0的情况）。

平方 [X−E(X)]2 可避免上述情况发生，但问题依据存在，不同的随机变量(比如，X,Y)之间在此级别是无法进行比较的，因为X,Y的数量空间是不同的（X可能有3个值，Y可能有1000个值），进而导致不具有可比性。 E{[X−E(X)]2} 则是将数量空间进行了统一，使得不同随机变量的方差具有了可比性。

ps : 方差的性质这里就不介绍了，可查看概率书籍。

　　标准差也是用于衡量一组数据的离散程度的。公式如下，可以看出标准差( σ(X) 表示 )于随机变量 X 处于同一量纲下，这为X以及 σ(X) 在同一公式中计算提供了很好的支持。 　　

　　前面一直在探讨单个随机变量（1维），但是事实上当我们考察一个群体的时候，往往事物的属性是多方面的（多维），这里只考察2维情况，形式如： (X,Y) 。 　　 　　 (X,Y) 的意思这类事物具有两个方面的属性，更进一步来说，一个样本有X,Y两方面的值，体现在数据库中，有两列（X列，Y列）。当Ｘ，Ｙ这两个属性出现在同一类事物中的时候，我们很自然想到Ｘ，Ｙ之间有某种关系，但是如何来刻画这种关系呢，这就是本节想要介绍的。 　　 　　 (X,Y) 是2维的，只考虑1维会无法从整体把握问题。而如果进行关联分析，有时候却需要对维度拆分来进行研究，这就引出了下面的协方差公式： 　　

其他关于协方差理解：【知乎】如何通俗易懂地解释「协方差」与「相关系数」的概念？

　　前面把比较关键的协方差说了一下，接下来说一下建立在协方差公式基础上的相关系数。简而言之，相关系数是对协方差进行了归一化处理，使其区间处于 [－１，１] 范围内。 　　下面看看相关系数 ρXY 的计算公式：

定理

为何 ρXY 反映的是线性相关性呢？ 这仍旧与前面的协方差相关，为了进一步探索，我们暂且先做出一个简单的假设：X,Y完全线性相关，那么接下来看看会发生什么神奇的事情呢？

再接下来，让我们放开那个非常强的假设（完全线性相关在现实生活中几乎不太可能存在，总会有些干扰的），去掉“完全”这个假设，留下“线性”这个假设。这里只是定性的分析下，定量的证明请参考数学书。 分母这里认为是正的，那么这里先只考虑分子的正负。

假如X,Y线性相关，接下来看看会对 Cov(X,Y)=E(XY)−E(X)E(Y) 造成什么影响。 这里我们设X是自由的，那么X确定之后，则限定了Y的自由活动的空间（见前面年龄、年级的例子），即Y不再自由了。造成的后果是

　　因为思想部分已经在协方差部分说了，这里不再赘述。

　　前面已经说了协方差的意义，协方差在于探索随机变量之间的关系。协方差矩阵计算的是不同维度之间的协方差。不是样本之间的关联关系。 　　 　　协方差探索的是随机变量X，Y之间的相关性，是放在同一个样本中来进行的。举一个简单的例子，学生小明（年龄17岁，年级为高2），小红（年龄17岁，年级为高3），小明、小红就是我们所说的样本，而年龄、年级则是随机变量。计算协方差时，考虑的是小明年龄和小明年级之间的关联关系（一个样本自身属性之间的关联关系）。 　　ps:未考虑小明、小红之间是否有关联关系（样本之间是否有关联关系）。 　　 　　当样本含有大量维度（随机变量多）的时候，我们就需要使用矩阵来刻画各个维度之间的关联关系。

PS: 个人感觉，协方差矩阵的计算是将整个维度系统中的制约关系，分解为两两之间的关系来进行刻画。

【假设】这其中隐藏了一个假设，在协方差矩阵的世界中认为，所有维度之间的关系都可以简化为两两之间的关系来进行研究。（正如牛顿的万有引力公式）

设谋个矩阵如下： （下面矩阵中每一行代表一个样本，每一列代表一个随机变量。）

则其协方差矩阵为：

关于协方差矩阵，此处不再赘述，可参看： [转]浅谈协方差矩阵 [线性代数] 如何求协方差矩阵 详解协方差与协方差矩阵

【知乎】排列组合的理解