学习资料： 传送门

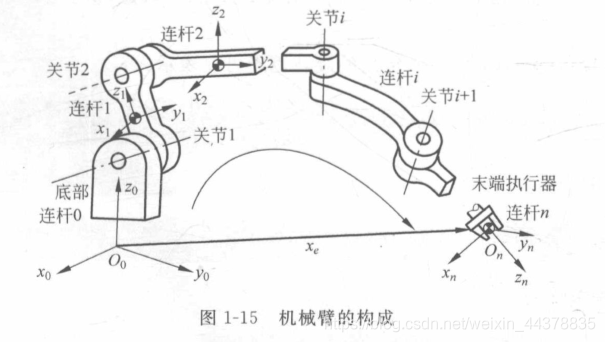
机器人本体,是机器人赖以完成作业任务的执行机构,一般是一台机械臂﹐也称操作臂或操作手,可以在确定的环境中执行控制系统指定的操作。典型工业机器人本体一般由

构成。机械臂多采用关节式机械结构，一般具有6个自由度,其中

机械臂上的末端执行装置可以根据操作需要换成焊枪﹑吸盘﹑扳手等作业工具。

如下图所示，一个机械臂是由一组可做相对运动的关节连接的连杆结合体。第一个连杆固定,连接该机械臂的基座,而最后一个连杆连接的是它的末端执行器。

通常可将关节划分为两种：

位于机械臂固定基座的坐标系称为基坐标系﹔位于操作臂末端执行器的坐标系称为工具坐标系,通常用它来描述机械臂的位置。

运动学是研究物体的运动,而不考虑物体的质量以及引起这种运动的力。

机器人正运动学：已知或给定一组关节角,计算出工具坐标系相对于基坐标系的位置和姿态,也就是说,用正运动学来确定机器人末端执行器的位姿。

机器人逆运动学：给定机械臂末端执行器的位置和姿态,计算所有可到达给定位置和姿态的关节角。也就是说,末端执行器在特定的一个点具有特定的姿态,去计算出它所对应的每一关节变量的值。

机器人运动学的研究方法,首先利用位姿描述,坐标系变换等数学方法确定物体位置、姿态和运动;然后确定不同结构类型的机器人的正逆运动学,这些类型包括直角坐标型、圆柱坐标型和球坐标型等等;最后根据 Denavit-Hartenberg 参数法去推导机器人的正逆运动学方程。

DH参数全称为Denavit-Hartenberg参数,它使用连杆参数来描述机构运动关系。如图1-17所示,在标准型DH参数法中,描述机械臂中的每一个连杆需要4个运动学参数,分别是连杆长度 a i − 1 a_{i-1} ai−1​ ,连杆转角 α i − 1 \alpha_{i-1} αi−1​，连杆偏距 d i d_i di​和关节角 θ i \theta_i θi​，它们的定义如下:

用以上4个参数对应转动关节和移动关节有两种情况:

在MATLAB机器人工具箱中,还用变量 σ i \sigma_i σi​,表示机器人的关节类型,其中 σ i = 0 \sigma_i=0 σi​=0表示转动关节， σ i = 1 \sigma_i=1 σi​=1表示移动关节(若未指定该参数﹐默认为转动关节)。在工具箱中,用函数Link()可以创建一个机械臂对象，其中输人的参数顺序分别是

例如,创建一个关节角初始为 θ i = 0 ° \theta_i=0° θi​=0°,连杆偏距 d i = 2 d_{i}=2 di​=2,连杆长度 a i − 1 = 3 a_{i-1}=3 ai−1​=3,连杆转角 α i − 1 = 45 ° \alpha_{i-1}= 45° αi−1​=45°，关节类型为转动关节的连杆。 输入命令：

运行结果 其中 , offset表示关节的偏移量。R表示为旋转关节,stdDH表示用标准型DH参数法去描述。用以下的命令可以获取连杆的各个参数。

创建一个平面三杠机械臂，因为它的三个关节均为转动关节，所以有时称该机械臂为RRR（或3R）机构。

三连杆平面机械臂的DH参数如下表所示： 输入命令：

通过构造函数SerialLink可以给创建的机械臂对象命名，并显示出对象的信息。 输入命令：

运行结果：

用以下命令可以获取已创建机械臂的各个参数：

首先应该确定两个关节上的坐标系,方法步骤如下: ① 将两个关节轴方向都定为第 i i i个坐标系和第 i 一 1 i一1 i一1个坐标系的 Z Z Z轴。

② 将两个关节轴之间公垂线方向定为第 i i i个坐标系的 X X X轴,而以公垂线第 i i i个关节轴上的交点作为原点。同理,第 i — 1 i—1 i—1个坐标系的 X X X轴和原点由之前两个坐标系公垂线共同确定。

③ 在已经确定坐标系 Z Z Z轴和 X X X轴的情况下﹐坐标系的 Y Y Y轴直接通过右手定则来确定。 对于初始轴(第0个轴) ,其与基座有关,可以自由定义,甚至可以与第1个关节轴重合，这样使第一个连杆长度 a 0 a_0 a0​、第一个转角 a 0 a_0 a0​置零,同时会简化正运动学的计算。

在机器人的每个关节上DH参数中的四个参数分别代表关节连杆不同的特征或在进行不同的变换。如图1-18所示,在某一瞬间,从第 i 一 1 i一1 i一1个关节到第 i i i个关节,经历的变换有: Z Z Z轴旋转( θ i \theta_i θi​)、 Z Z Z轴平移( d i d_{i} di​) ,X轴平移( a i a_{i} ai​)和 X X X轴旋转( α i \alpha_{i} αi​)。

将之前的齐次变换矩阵 T T T和DH参数联系起来，即可得到（ i − 1 i-1 i−1全部改成 i i i）：

MATLAB机器人工具箱用矩阵A表示T：

运行结果：

所以这个变换矩阵为

首先应该确定两个关节上的坐标系,方法步骤如下: ① 将两个关节轴方向都定为第 i i i个坐标系和第 i 一 1 i一1 i一1个坐标系的 Z Z Z轴。

② 将两个关节轴之间公垂线方向定为第 i − 1 i-1 i−1个坐标系的 X X X轴,而以公垂线第 i − 1 i-1 i−1个关节轴上的交点作为原点。同理,第 i i i个坐标系的 X X X轴和原点由之后两个坐标系公垂线共同确定。 ③ 在已经确定坐标系 Z Z Z轴和 X X X轴的情况下﹐坐标系的 Y Y Y轴直接通过右手定则来确定。 对于初始轴(第0个轴) ,其与基座有关,可以自由定义,甚至可以与第1个关节轴重合，这样使第一个连杆长度 a 0 a_0 a0​、第一个转角 a 0 a_0 a0​置零,同时会简化正运动学的计算。

改进型DH参数描述法对坐标系变换如图1-19所示,在某一瞬间,从第 i 一 1 i一1 i一1个关节到第 i i i个关节,经历的变换有: X X X轴旋转( α i − 1 \alpha_{i-1} αi−1​), X X X轴平移( a i − 1 a_{i-1} ai−1​)、Z轴旋转( θ i \theta_i θi​)和 Z Z Z轴平移( d i d_i di​)。所以,对应的变换矩阵为: 因此：

在创建连杆对象时，使用改进型DH描述法需要指定参数为modified 输入命令：

运行结果：

所以这个变换矩阵：

通过将一个连杆的变换矩阵连乘能够得到坐标 { N } \{N\} {N}相对于坐标 { 0 } \{0\} {0}的变换矩阵：

这个变换矩阵是 N N N个关节变量的函数。

回顾正运动学的概念:给定一组关节角,计算出工具坐标系相对于基坐标系的位置和姿态。在这里,可以通过各个关节位置传感器得到所需要的值,然后求出每个连杆的变换矩阵,通过上式就可求出机器人末端的工具坐标系相对于基坐标系的位姿,可表示为: 上面的等式中的 r r r,即三行三列的子矩阵代表从基座到末端执行器的旋转矩阵,其中的

MATLAB机器人工具箱中用了函数fkine()计算正运动学的问题。以上面的三连杆平面机械臂为例,用标准型DH参数描述法计算。

运行结果： 所以机械臂初始状态为：

将创建的机械臂用图像化显示出来。输入命令：

当第二个关节旋转30°，第三个关节旋转45°时，可视化：

机器人逆运动学的问题即已知机械臂末端的工具坐标系相对于基坐标系的位置和姿态,计算所有能够到达给定位置和姿态的关节角﹐即已知变换矩阵 N 0 T _N^0T N0​T,计算出能够得到 N 0 T _N^0T N0​T的一系列关节角 θ 1 , θ 2 , θ 3 , . . . , θ n \theta_1,\theta_2,\theta_3,...,\theta_n θ1​,θ2​,θ3​,...,θn​

对于以上的问题，有以下几种情况：

(1) 不存在相应的解。当所期望的位姿离基坐标系太远,而机械臂不够长时,末端执行器无法达到该位姿﹔当机械臂的自由度少于6个自由度时,它将不能达到三维空间的所有位姿﹔此外,对于实际中的机械臂,关节角不一定能到达360°,使得它不能达到某些范围内的位姿。在以上的情况中,机械臂都不能达到某些给定的位姿,因此不存在解。

(2) 存在唯一的解。当机械臂只能从一个方向达到期望的位姿时,只存在一组关节角使得它能到达这个位姿,即存在唯一的解。

(3) 存在多个解。当机械臂能从多个方向达到期望的位姿时,存在着多组关节角能使得它到达这个位姿,即存在多个解。此时,需要选择一组最适合的解:

对机器人的运动学方程进行求解,是一个非线性问题。目前对这个问题的求解方法分为两种:封闭解法和数值解法。

在封闭解法中,使用ikine6s()求解逆运动学的问题,它只适用于关节数为6,且腕部三个旋转关节的轴相交于一个点的情况。这种解法使用显式控制的方法对机械臂运动学进行配置,使得在存在多个解的情况下,能够指定一定的配置,得到一个唯一的解。函数ikine6s()使用以下标志符进行相应的配置: 以KUKA KR5机器人为例，对机器人的逆运动学问题进行数值解法的求解。 加载机器人KR5模型：

显示机器人的具体参数：

首先，使用正运动学的方法，让机器人按下列的关节旋转，达到一定的位姿 T T T：

以 T T T为已知条件，用封闭解的方法求出相应的旋转关节角：

运行结果： 可以看到,得到的一组关节角与之前的关节角不一样,但这两组关节角显然能够达到相同的末端执行器位姿。此时可以指定配置,得到一个目标解。 输入命令：

可以看到，虽然关节角不同，但是末端执行器的位姿相同。

数值解的方法使用ikine()求解逆运动学的问题,它可适用于各种关节数目的机械臂通过设定初始的关节角坐标对机械臂运动学配置进行隐式控制。

以puma560机器人为例,对机器人的逆运动学问题进行数值解法的求解。加载机器人模型,并输入一组关节角﹐输入命令:

未设定初始关节角坐标，使用ikine()进行求解：

设定初始关节角坐标，使用ikine()进行求解：

正运动学的内容主要研究如何定位末端执行器,即得到基坐标系中如何描述末端执行器的位姿.当机械臂开始运动时,其中各个关节上的编码器会即时记录并监控微分运动,如果在当前位姿下把末端执行器移动一段很小的位移,就会得到末端执行器一个特定的位姿。

假设末端执行器的位姿为 x x x，关节角 θ \theta θ，则线速度 x ˙ \dot{x} x˙，关节角速度为 θ ˙ \dot{\theta} θ˙。

可以通过一个矩阵将两者联系在一起，这个矩阵就是雅可比矩阵

机械臂的位姿 x x x与关节变量 q q q的函数关系是： 即 上式两边分别计算其速度，需要使用微分和偏微分，并用矩阵形式表示： 用机械臂末端在笛卡尔空间的速度 x ˙ \dot{x} x˙表示 δ x m × 1 \delta x_{m\times 1} δxm×1​,用关节速度 q ˙ \dot{q} q˙​表示 δ q n × 1 \delta q_{n\times 1} δqn×1​，则机械臂的雅可比矩阵定义为机械臂末端的笛卡尔速度与关节速度的线性变换，用公式表示如下：

其中， J ( q ) J(q) J(q)为机械臂的雅可比矩阵,为一个 m × n m\times n m×n的偏导数矩阵．操控机器人时,想得到微分运动 δ x \delta x δx所对应的 δ q \delta q δq，可用下式：

将末端执行器的线速度 ( v x , v y , v z ) (v_x,v_y,v_z) (vx​,vy​,vz​)和角速度 w x , w y , w z w_x,w_y,w_z wx​,wy​,wz​这6个变量作为雅可比矩阵等式的左边，即：

上式中， n n n代表机器人的自由度， J 0 J_0 J0​在运动学中起着非常重要的作用，可以用于对速度的表述。因为所有对速度的表述都与线速度和角速度相关，任何与速度相关的表述都可以和这个雅可比矩阵建立联系。

将这个雅可比矩阵去掉下标（即 J J J）作为基本雅可比矩阵，这个矩阵建立了线速度及角速度与关节角速度之间的关系。根据这种关系可将雅可比矩阵 J J J分为两部分，即：

对于 J v J_v Jv​，即为联系关节角速度和末端执行器线速度的矩阵。在笛卡尔坐标中，由前面齐次转换矩阵 T T T可知，矩阵 T T T的最后一列中的前三个变量 ( p x , p y , p z ) (p_x,p_y,p_z) (px​,py​,pz​)表示末端执行器或者物体最后一个关节坐标系相对于基座参考坐标系的位置，将这三个变量统一表示为一个位置变量 x p x_p xp​，则线速度可以表示为：

x p ( q 1 , q 2 , . . . q n ) x_p(q_1,q_2,...q_n) xp​(q1​,q2​,...qn​) 从中可得：

上式即为与线性运动相关的雅可比矩阵 J v J_v Jv​。当然，从结构定义可知，上式是指当关节为转动关节时的矩阵，当机器人关节为移动关节时，其对应的变量为0.

对于矩阵 J w J_w Jw​，即为联系关节角速度末端执行器角速度的矩阵。角速度可以表示为： 从中可得：

上式中， ε ‾ = 1 − ε \overline{\varepsilon}=1-\varepsilon ε=1−ε，当关节为转动关节时， ε i = 0 \varepsilon_i=0 εi​=0，当关节为移动关节时， ε i = 1 \varepsilon_i=1 εi​=1。

对于每个机器人关节，旋转都是指绕 Z Z Z轴的旋转，而 z i z_i zi​则是指齐次变换矩阵 i 0 T ^0_iT i0​T中的第三列前三个变量表示为一个旋转变量，即

分别得到 J v J_v Jv​和 J w J_w Jw​之后，最终就得到了需要的反映末端执行器线速度和角速度的雅可比矩阵。

在MATLAB机器人工具箱中 SerialLink.jacob0()：可求出对应某个位姿下世界坐标系中的雅可比矩阵

SerialLink.jacobn()：可求出对应某个位姿下工具坐标系中的雅可比矩阵。

以KUKA KR5机器人为例，给定一组关节角， q = [ 0 , p i / 4 , p i , 0 , p i / 4 , 0 ] q=[0,pi/4 ,pi,0,pi/4,0] q=[0,pi/4,pi,0,pi/4,0]，求出在该位姿下的雅可比矩阵。

已知坐标系 B {B} B中， 6 × 1 6\times 1 6×1的笛卡尔速度矢量可以通过以下变换得到在坐标系 A {A} A中的变换： 已知坐标系 A {A} A、 B {B} B中的雅可比矩阵分别为： 因此，可以得到雅可比矩阵参考坐标系的变换：

同样以KUKA KR5机器人为例：

可以看出，结果与 J 0 J_0 J0​指相同。

当坐标系 A {A} A和坐标系 B {B} B是刚性连接时，且 A {A} A通过旋转矩阵，再通过平移矢量得到 B {B} B时，通过下式可以得到速度在两个坐标系中表示的变换。

写成矩阵形式为：

这里， A B T ^B_AT AB​T为一个 6 × 6 6\times 6 6×6的速度变换矩阵。

在MATLAB机器人工具箱中，可用函数tr2jac()求出不同变换的雅可比矩阵。例如， B {B} B是通过 A {A} A平移 ( 2 , 4 , 0 ) (2,4,0) (2,4,0)，再旋转45°得到的，求速度变换矩阵 T v T_v Tv​。当 A {A} A中 X X X方向的线速度为 2 m / s 2m/s 2m/s，求{B}中的速度。

可以得到，该速度在 B {B} B中 X X X方向为 1.4142 m / s 1.4142m/s 1.4142m/s，在 Z Z Z方向速度为 1.4142 m / s 1.4142m/s 1.4142m/s。

与Link对象相关方法如下：

写入/读取Link的参数如下所示：

Link：创建机器人的连杆对象 (1)L= Link()是具有默认参数的Link对象; (2)L= Link(link)是一个Link对象,它是连杆对象link的副本;(3)L= Link( options)是指定了运动和动态参数的连杆对象。

options:

SerialLink类包含的参数：

写入/读取SerialLink类的参数如下所示：

SerialLink：创建一个SerialLink机器人对象

(1)R= SerialLink(links, options)是一个由Link类对象定义的机器人对象,它可以是Link,Revolute,Prismatic,RevoluteMDH 或PrismaticMDH的实例。 (2)R = SerialLink(options)是一个没有连杆的空机器人对象。 (3)R = SerialLink([R1 R2…],选项)连接机器人,R2的基座连接到Rl的末端。也可以写成R1*R2 (4)R = SerialLink(R1,选项)是机器人对象R1的深层副本,具有所有相同的属性。 (5)R = SerialLink(dh, options)是具有由矩阵dh定义的运动学的机器人对象,其中每个关节具有一行,并且每一行是Ga并且假设关节被旋转。可选的第五列sigma指示旋转(sigma = 0,默认)或移动(sigma = 1)。

它的参数如下：

《机器人仿真与编程技术》 杨辰光 李智军 许扬