从数理统计简史中看正态分布的历史由来 |
您所在的位置:网站首页 › 正态分布的由来和发展 › 从数理统计简史中看正态分布的历史由来 |
从数理统计简史中看正态分布的历史由来
|
相信,你我可以想象得到,我们现在眼前所看到的正态分布曲线虽然看上去很美,但数学史上任何一个定理的发明几乎都不可能一蹴而就,很多往往经历了几代人的持续努力。因为在科研上诸多观念的革新和突破是有着很多的不易的,或许某个定理在某个时期由某个人点破了,现在的我们看来一切都是理所当然,但在一切没有发现之前,可能许许多多的顶级学者毕其功于一役,耗尽一生,努力了几十年最终也是无功而返。
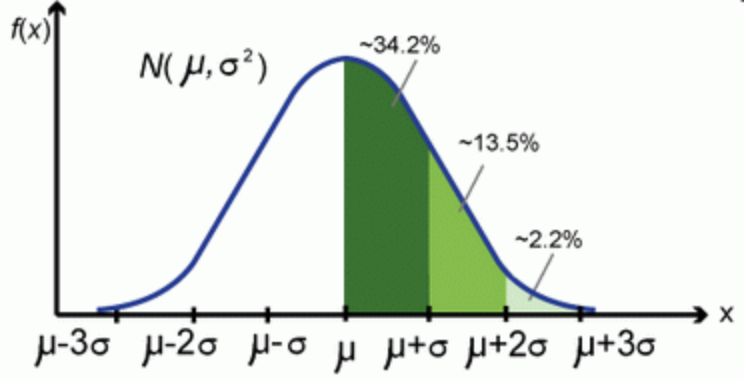
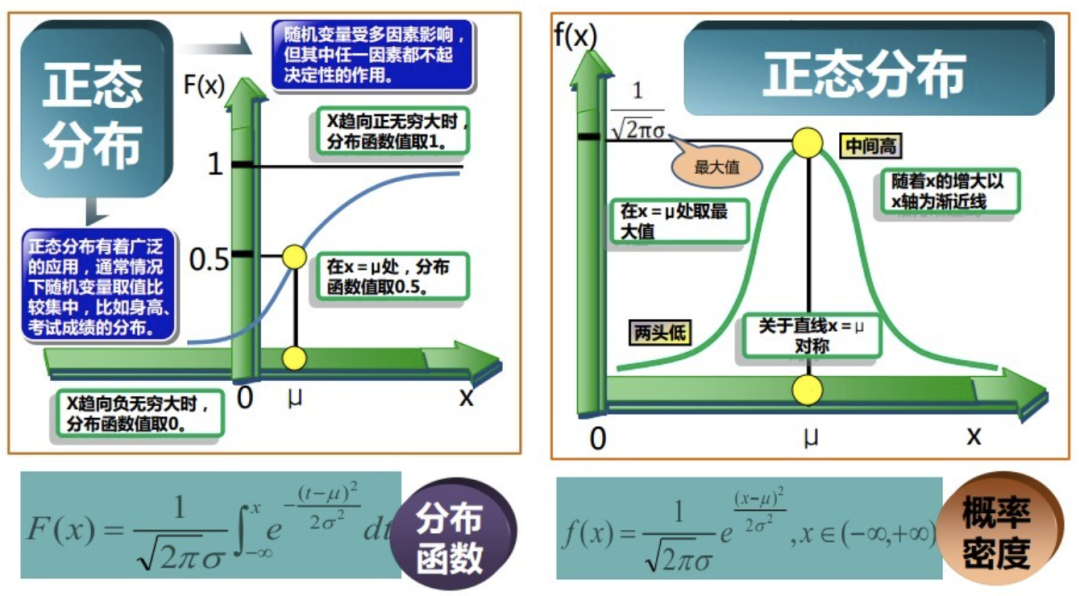
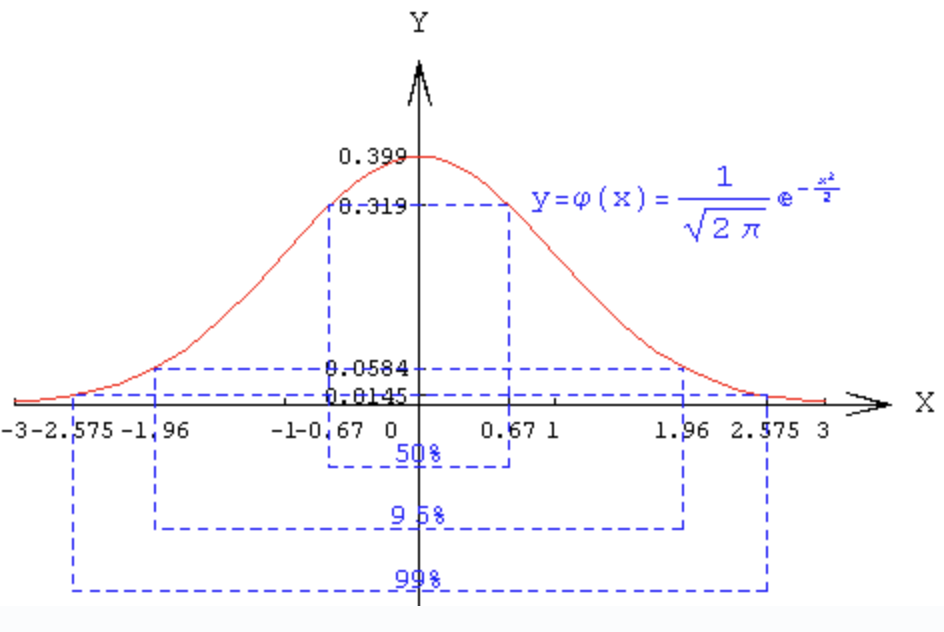
如上文前三节所见,现在概率论与数理统计的教材上,一上来介绍正态分布,然后便给出其概率密度分布函数,却从来没有说明这个分布函数是通过什么原理推导出来的。如此,可能会导致你我在内的很多人一直搞不明白数学家当年是怎么找到这个概率分布曲线的,又是怎么发现随机误差服从这个奇妙的分布的。我们在实践中大量的使用正态分布,却对这个分布的来龙去脉知之甚少。 本文接下来的第四节将结合陈希儒院士的《数理统计学简史》及“正态分布的前世今生”为你揭开正态分布的神秘面纱。 4.1 正态分布的定义 上文中已经给出了正态分布的相关定义,咱们先再来回顾下。如下两图所示(来源:大嘴巴漫谈数据挖掘):
相信,经过上文诸多繁杂公式的轰炸,读者或有些许不耐其烦,咱们接下来讲点有趣的内容:历史。下面,咱们来结合数理统计简史一书,及正态分布的前世今生系列,从古至今论述正态分布的历史由来。 4.2 早期概率论:从萌芽到推测术 4.2.1 惠更新的三个关于期望的定理 (一) 惠更新的论赌博的计算 所谓概率,即指一个事件发生,一种情况出现的可能性大小的数量指标,介于0和1之间,这个概念最初形成于16世纪,说来可能令你意想不到,凡事无绝对,早期很多概率论中的探讨却与掷骰子等当今看来是违法犯罪的赌博活动有着不可分割的联系,可以说,这些赌博活动反而推动了概率论的早期发展。 历史是纷繁多杂的,咱们从惠更斯的机遇的规律一书入手,此人指导过微积分的奠基者之一的莱布尼兹学习数学,与牛顿等人也有交往,终生未婚。如诸多历史上有名的人物一般,他们之所以被后世的人们记住,是因为他们在某一个领域的杰出贡献,这个贡献可能是提出了某一个定理或者公式,换句话来说,就是现今人们口中所说的代表作,一个意思。 而惠更新为当代人们所熟知的应该是他在《摆式时钟或用于时钟上的摆的运动的几何证明》、《摆钟》等论文中提出了物理学史上钟摆摆动周期的公式: (二) 创立数学期望 与此同时,惠更斯1657年发表了《论赌博中的计算》,被认为是概率论诞生的标志。同时对二次曲线、复杂曲线、悬链线、曳物线、对数螺线等平面曲线都有所研究。 《论赌博中的计算》中,惠更斯先从关于公平赌博值的一条公理出发,推导出有关数学期望的三个基本定理,如下述内容所示: 公理:每个公平博弈的参与者愿意拿出经过计算的公平赌注冒险而不愿拿出更多的数量。即赌徒愿意押的赌注不大于其获得赌金的数学期望数。 对这一公理至今仍有争议。所谓公平赌注的数额并不清楚,它受许多因素的影响。但惠更斯由此所得关于数学期望的3个命题具有重要意义。这是数学期望第一次被提出,由于当时概率的概念还不明确,后被拉普拉斯(Laplace,1749—1827)用数学期望来定义古典概率。在概率论的现代表述中,概率是基本概念,数学期望则是二级概念,但在历史发展过程中却顺序相反。 关于数学期望的三个命题为: 命题1:若某人在赌博中以等概率1/2获得赌金a元、b元,则其数学期望值为:a*1/2+b*1/2,即为(a+b)/2; 命题2:若某人在赌博中以等概率1/3获得赌金a、b元和c元,则其数学期望值为(a+b+c)/3元; 命题3:若某人在赌博中以概率p和q (p≥0,q≥0,p+q=1)获得赌金a元、b元,则获得赌金的数学期望值为p*a+q*b元。 这些今天看来都可作为数学期望定义,不准确的说,数学期望来源于取平均值。同时,根据上述惠更斯的3个命题不难证明:若某人在赌博中分别以概率p1...,pk(p1+..+pk=1)分别赢得a1,..ak元,那么其期望为p1*a1+...+pk*ak,这与本文第一节中关于离散型随机变量的期望的定义完全一致(各值与各值概率乘积之和)。 但惠更新关于概率论的讨论局限于赌博中,而把概率论由局限于对赌博机遇的讨论扩展出去的则得益于伯努利,他在惠更新的论赌博中的计算一书出版的56年,即1733年出版了划时代的著作:推测术。伯努利在此书中,不仅对惠更斯的关于掷骰子等赌博活动中出现的额各种情况的概率进行了计算,而且还提出了著名的“大数定律”,这个定律在历史上甚至到今天,影响深远,后续诸多的统计方法和理论都是建立在大数定律的基础上。 (三) 伯努利的大数定律及其如何而来 同样,咱们在读中学的时候,之所以记住了伯努利这个人,恐怕是因为物理课上,老师所讲的伯努利方程 当然,伯努利的贡献不仅在此,而在于他的大数定律。那何谓伯努利大数定律呢? 设在n次独立重复试验中,事件X发生的次数为。事件X在每次试验中发生的概率为P。则对任意正数,下式成立:
定理表明事件发生的频率依概率收敛于事件的概率。定理以严格的数学形式表达了频率的稳定性。就是说当n很大时,事件发生的频率于概率有较大偏差的可能性很小。 这个定理如何而来的呢? 咱们来看一个简单的袋中抽球的模型,袋中有a个白球,b个黑球,则从袋中取出白球的概率为p=a/(a+b),有放回的充袋中抽球N次(每次抽取时保证袋中a+b个球的每一个都有同等机会被抽出),记得抽到的白球的次数为X,然后以X/N这个值去估计p,这个估计方法至今仍是数理统计学中最基本的方法之一。 伯努利试图证明的是:用X/N估计p可以达到事实上的确定性,即:任意给定两个数ε>0和η>0,取足够大的抽取次数N,使得事件 换句话说,我们需要证明的是当N充分无限大时,X/N无限逼近于p,用公式表达即为:
尽管现在我们看来,上述这个结论毫无疑问是理所当然的,但直到1909年才有波莱尔证明。此外,此伯努利大数定律是我们今天所熟知的契比雪夫不等式的简单推论,但须注意的是在伯努利那个时代,并无“方差”这个概念,更不用说从这个不等式而推论出伯努利大数定律了。 此外,常用的大数定律除了伯努利大数定律之外,还有辛钦大数定律、柯尔莫哥洛夫强大数定律和重对数定律等定律。这里稍微提下辛钦大数定律,如下图所示。
在1733年,棣莫弗发展了用正态分布逼近二项分布的方法,这对于当时而言,是一实质性的深远改进。 4.3 棣莫弗的二项概率逼近 同上文中的惠更新,伯努利一样,人们熟悉棣莫弗,想必是因为著名的棣莫弗公式,如下:
据数理统计学简史一书上的说明,棣莫弗之所以投身到二项概率的研究,非因伯努利之故,而又是赌博问题(赌博贡献很大丫哈)。有一天一个哥们,也许是个赌徒,向棣莫弗提了一个和赌博相关的一个问题:A、B两人在赌场里赌博,A、B各自的获胜概率是p和q=1−p,赌n局,若A赢的局数X>np,则A付给赌场X−np元,否则B付给赌场np−X元。问赌场挣钱的期望值是多少?按定义可知,此期望值为:
上式的b(N,平,i)为二项概率,棣莫弗最终在Np为整数的条件下得到:
当m=N/2时,N趋于无穷:
也就是说上述问题的本质上是上文第一节中所讲的一个二项分布。虽然从上述公式可以集结此问题,但在N很大时,计算不易,故棣莫弗想找到一个更方便于计算的近似公式。 棣莫弗后来虽然做了一些计算并得到了一些近似结果,但是还不够,随后有人讲棣莫弗的研究工作告诉给了斯特林,于是,便直接催生了在数学分析中必学的一个重要公式斯特林公式(斯特林公式最初发表于1730年,而后棣莫弗改进了斯特林公式):
1733年,棣莫弗有了一个决定性意义的举动,他证明了当N趋于去穷时,有下列式子成立:
不要小瞧了这个公式。当它与上面给出的这个公式
根据上面式子,近似地以定积分代替和,得到下式:
不知道,当读者读到这里的时候,是否从上式看出了些许端倪,此式可隐藏了一个我们习以为常却极其重要的概念。OK,或许其形式不够明朗,借用rickjin的式子转化下:
没错,正态分布的概率密度(函数)在上述的积分公式中出现了!于此,我们得到了一个结论,原来二项分布的极限分布便是正态分布。与此同时,还引出了统计学史上占据重要地位的中心极限定理。 棣莫弗-拉普拉斯定理:设随机变量Xn(n=1,2...)服从参数为p的二项分布,则对任意的x,恒有下式成立:
我们便称此定理为中心极限定理。而且还透露着一个极为重要的信息:1730年,棣莫弗用二项分布逼近竟然得到了正太密度函数,并首次提出了中心极限定理。 还没完,随后,在1744年,拉普拉斯证明了:
最终,1780年,拉普拉斯建立了中心极限定理的一般形式(也就是上文3.2节中所讲的中心极限定理的一般形式): Lindeberg-Levy中心极限定理:设X1,⋯,Xn独立同分布,且具有有限的均值μ和方差σ2,则在n→∞时,有:
棣莫弗的工作对数理统计学有着很大的影响,棣莫弗40年之后,拉普拉斯建立中心极限定理的一般形式,20世纪30年代最终完成独立和中心极限定理最一般的形式,在中心极限定理的基础之上,统计学家们发现当样本量趋于无穷时,一系列重要统计量的极限分布如二项分布,都有正态分布的形式,也就是说,这也构成了数理统计学中大样本方法的基础。 此外,从上面的棣莫弗-拉普拉斯定理,你或许还没有看出什么蹊跷。但我们可以这样理解:若取c充分大,则对足够大的N,事件
而这就是上文中所讲的伯努利大数定律(注:上面讨论的是对称情况,即p=1/2的情况)。 我之所以不厌其烦的要论述这个棣莫弗的二项概率逼近的相关过程,是想说明一点:各个定理、公式彼此之前是有着紧密联系的,要善于发现其中的各种联系。 同时,还有一个问题,相信读者已经意识到了,如本文第一节内容所述,咱们的概率论与数理统计教材讲正态分布的时候,一上来便给出正态分布的概率密度(函数),然后告诉我们说,符合这个概率密度(函数)的称为正态分布,紧接着阐述和证明相关性质,最后说了一句:”在自然现象和社会现象中,大量随机变量都服从或近似服从正态分布,如人的身高,某零件长度的误差,海洋波浪的高度“,然后呢?然后什么也没说了。连正态分布中最基本的两个参数为、和的的意义都不告诉我们(位置参数即为数学期望,尺度参数为即为方差,换句话说,有了期望和方差,即可确定正态分布)。
随后,教材上便开始讲数学期望,方差等概念,最后才讲到中心极限定理。或许在读者阅读本文之后,这些定理的先后发明顺序才得以知晓。殊不知:正态分布的概率密度(函数)形式首次发现于棣莫弗-拉普拉斯中心极限定理中,即先有中心极限定理,而后才有正态分布(通过阅读下文4.6节你将知道,高斯引入正太误差理论,才成就了正态分布,反过来,拉普拉斯在高斯的工作之上用中心极限定理论证了正态分布)。 如rickjin所言:’‘学家研究数学问题的进程很少是按照我们数学课本的安排顺序推进的,现代的数学课本都是按照数学内在的逻辑进行组织编排的,虽然逻辑结构上严谨优美,却把数学问题研究的历史痕迹抹得一干二净。DNA双螺旋结构的发现者之一JamesWaston在他的名著《DNA双螺旋》序言中说:‘科学的发现很少会像门外汉所想象的一样,按照直接了当合乎逻辑的方式进行的。’’‘ 4.4 贝叶斯方法 前面,介绍了惠更斯、伯努利和棣莫弗等人的重大成果,无疑在这些重要发明中,二项分布都占据着举重轻重的地位。这在早期的概率统计史当中,也是唯一一个研究程度很深的分布。但除了伯努利的大数定律及棣莫弗的二项逼近的研究成果外,在18世纪中叶,为了解决二项分布概率的估计问题,出现了一个影响极为广泛的贝叶斯方法,贝叶斯方法经过长足的发展,如今已经成为数理统计学中的两个主要学派之一:贝叶斯学派,牢牢占据数理统计学领域的半壁江山。 据数理统计学简史一书,托马斯.贝叶斯,此人在18世纪上半叶的欧洲学术界,并不算得上很知名,在提出贝叶斯定理之前,也未发表过片纸只字的科学论著,套用当今的话来说,他便是活生生一个民间学术屌丝。
未发表过任何科学著作,但一个人如果热爱研究,喜好学术的话,必找人交流。于此,诸多重大发明定理都出现在学者之间的一些书信交流中。奇怪的是,贝叶斯这方面的书信材料也不多。或许读者读到此处,已知我意,会说这一切在他提出贝叶斯定理之后有了改变,但读者朋友只猜对了一半。 贝叶斯的确发表了一篇题为Anessaytowardssolvingaprobleminthedoctrineofchances(机遇理论中一个问题的解)的遗作,此文在他发表后很长一段时间起,在学术界没有引起什么反响,直到20世纪以来,突然受到人们的重视,此文也因此成为贝叶斯学派最初的奠基石(又一个梵高式的人物)。 有人说贝叶斯发表此文的动机是为了解决伯努利和棣莫弗未能解决的二项分布概率P的“逆概率”问题。所谓逆概率,顾名思义,就是求概率问题的逆问题:已知时间的概率为P,可由之计算某种观察结果的概率如何;反过来,给定了观察结果,问由之可以对概率P作何推断。也就是说,正概率是由原因推结果,称之为概率论;而逆概率是结果推原因,称之为数理统计。 由于本文中,重点不在贝叶斯定理,而本文第一节之2.1小节已对其做简要介绍,再者,此文从决策树学习谈到贝叶斯分类算法、EM、HMM第二部分也详细介绍过了贝叶斯方法,故为本文篇幅所限,不再做过多描述。 4.5 最小二乘法,数据分析的瑞士军刀 事实上,在成百上千的各式各样的攻击方法中,取算术平均恐怕是最广为人知使用也最为广泛的方法,因为可能一个小学生都知道使用算术平均来计算自己每天平均花了多少零花钱而以此作为向爸妈讨要零花钱的依据。而我们大多数成年人也经常把“平均说来”挂在嘴边。故此节要讲的最小二乘法其实并不高深,它的本质思想即是来源于此算术平均的方法。 不太精确的说,一部数理统计学的历史,就是从纵横两个方向对算术平均进行不断深入研究的历史, 纵的方面指平均值本身,诸如伯努利及其后众多的大数定律,棣莫弗-拉普拉斯中心极限定理,高斯的正太误差理论,这些在很大程度上都可以视为对算术平均的研究成果,甚至到方差,标准差等概念也是由平均值发展而来; 横的方面中最为典型的就是此最小二乘法。 而算术平均也是解释最小二乘法的最简单的例子。使误差平方和达到最小以寻求估计值的方法,则称为最小二乘估计(当然,取平方和作为目标函数知识众多可取的方法之一,例如也可以取误差4次方或绝对值和,取平方和是人类千百年实践中被证实行之有效的方法,因此被普遍采用)。 何谓最小二乘法?实践中,常需寻找两变量之间的函数关系,比如测定一个刀具的磨损速度,也就是说,随着使用刀具的次数越多,刀具本身的厚度会逐渐减少,故刀具厚度与使用时间将成线性关系,假设符合f(t)=at+b(t代表时间,f(t)代表刀具本身厚度),a,b是待确定的常数,那么a、b如何确定呢? 最理想的情形就是选取这样的a、b,能使直线y=at+b所得到的值与实际中测量到的刀具厚度完全符合,但实际上这是不可能的,因为误差总是存在难以避免的。故因误差的存在,使得理论值与真实值存在偏差,为使偏差最小通过偏差的平方和最小确定系数a、b,从而确定两变量之间的函数关系f(t)=at+b。 这种通过偏差的平方和为最小的条件来确定常数a、b的方法,即为最小二乘法。最小二乘法的一般形式可表述为:
在此,说点后话,最小二乘法是与统计学有着密切联系的,因为观测值有随机误差,所以它同正态分布一样与误差论有着密切联系(说实话,最小二乘法试图解决的是误差最小的问题,而正态分布则是试图寻找误差分布规律的问题,无论是最小二乘法,还是正态分布的研究工作,至始至终都围绕着误差进行)。 那么,最小二乘法是如何发明的呢?据史料记载,最小二乘法最初是由法国数学家勒让德于1805年发明的。那勒让德发明它的动机来源于哪呢? 18世纪中叶,包括勒让德、欧拉、拉普拉斯、高斯在内的许多天文学家和数学家都对天文学上诸多问题的研究产生了浓厚的兴趣。比如以下问题: 土星和木星是太阳系中的大行星,由于相互吸引对各自的运动轨道产生了影响,许多大数学家,包括欧拉和拉普拉斯都在基于长期积累的天文观测数据计算土星和木星的运行轨道。 勒让德承担了一个政府给的重要任务,测量通过巴黎的子午线的长度。 海上航行经纬度的定位。主要是通过对恒星和月面上的一些定点的观测来确定经纬度。 这些问题都可以用如下数学模型描述:我们想估计的量是β0,⋯,βp,另有若干个可以测量的量x1,⋯,xp,y,这些量之间有线性关系
如何通过多组观测数据求解出参数β0,⋯,βp呢?欧拉和拉普拉斯采用的都是求解线性方程组的方法。
但是面临的一个问题是,有n组观测数据,p+1个变量,如果n>p+1,则得到的线性矛盾方程组,无法直接求解。所以欧拉和拉普拉斯采用的方法都是通过一定的对数据的观察,把n个线性方程分为p+1组,然后把每个组内的方程线性求和后归并为一个方程,从而就把n个方程的方程组化为p+1个方程的方程组,进一步解方程求解参数。这些方法初看有一些道理,但是都过于经验化,无法形成统一处理这一类问题的一个通用解决框架。 以上求解线性矛盾方程的问题在现在的本科生看来都不困难,就是统计学中的线性回归问题,直接用最小二乘法就解决了,可是即便如欧拉、拉普拉斯这些数学大牛,当时也未能对这些问题提出有效的解决方案。可见在科学研究中,要想在观念上有所突破并不容易。有效的最小二乘法是勒让德在1805年发表的,基本思想就是认为测量中有误差,所以所有方程的累积误差为:
我们求解出导致累积误差最小的参数即可。
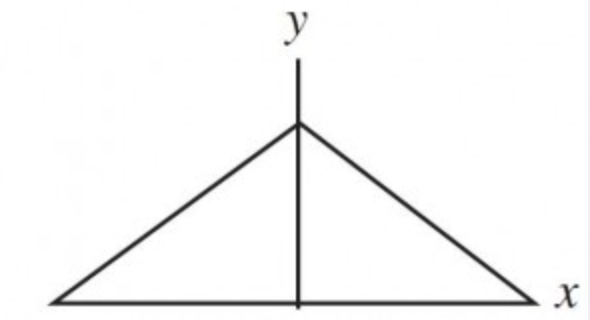
上面我们已经看到,是勒让德最初发明的最小二乘法,那为何历史上人们常常把最小二乘法的发明与高斯的名字联系起来呢?(注:勒让德时期的最小二乘法还只是作为一个处理测量数据的代数方法来讨论的,实际上与统计学并无多大关联,只有建立在了测量误差分布的概率理论之后,这个方法才足以成为一个统计学方法。尽管拉普拉斯用他的中心极限定理定理也可以推导出最小二乘法,但无论是之前的棣莫弗,还是当时的勒让德,还是拉普拉斯,此时他们这些研究成果都还只是一个数学表达式而非概率分布)。 因为1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,即为高斯-马尔可夫定理。也就是说勒让德最初提出了最小二乘法,而却是高斯让最小二乘法得以巩固而影响至今。且高斯对最小二乘法的最大贡献在于他是建立在正太误差分布的理论基础之上的(后续更是导出了误差服从正态分布的结论),最后,1837年,统计学家们正式确立误差服从正态分布,自此,人们方才真正确信:观测值与理论值的误差服从正态分布。 4.6 误差分布曲线的建立 十八世纪,天文学的发展积累了大量的天文学数据需要分析计算,应该如何来处理数据中的观测误差成为一个很棘手的问题。我们在数据处理中经常使用平均的常识性法则,千百年来的数据使用经验说明算术平均能够消除误差,提高精度。平均有如此的魅力,道理何在,之前没有人做过理论上的证明。算术平均的合理性问题在天文学的数据分析工作中被提出来讨论:测量中的随机误差应该服从怎样的概率分布?算术平均的优良性和误差的分布有怎样的密切联系? 伽利略在他著名的《关于两个主要世界系统的对话》中,对误差的分布做过一些定性的描述,主要包括: 误差是对称分布的分布在0的两侧: 大的误差出现频率低,小的误差出现频率高。 用数学的语言描述,也就是说误差分布函数f(x)关于0对称分布,概率密度随|x|增加而减小,这两个定性的描述都很符合常识。 4.6.1 辛普森的工作 许多天文学家和数学家开始了寻找误差分布曲线的尝试。托马斯•辛普森(ThomasSimpson,1710-1761)先走出了有意义的一步。 设真值为θ,而 但若用算术平均 Simpson证明了,对于如下的一个概率分布:
Simpson的误差态分布曲线有这样的估计:
也就是说, 4.6.2 拉普拉斯的工作 在1772-1774年间,拉普拉斯也加入到了寻找误差分布函数的队伍中。与辛普森不同,拉普拉斯不是先假定一种误差分后去设法证明平均值的优良性,而是直接射向应该去怎么的分布为误差分布,以及在确定了误差分布之后,如何根据观测值 拉普拉斯假定误差密度函数f(x)满足如下性质:
m>0,且为常数,上述方程解出 |
【本文地址】
今日新闻 |
点击排行 |
|
推荐新闻 |
图片新闻 |
|
专题文章 |

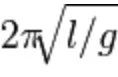 。
。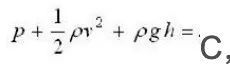 ,(C为常量)。
,(C为常量)。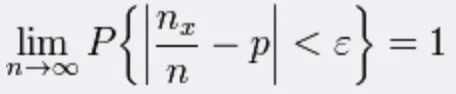
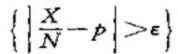 的概率不超过η,这意思是
的概率不超过η,这意思是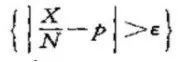 ,表面估计误差未达到制定的接近程度η。
,表面估计误差未达到制定的接近程度η。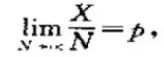 (N趋于无穷大)
(N趋于无穷大)
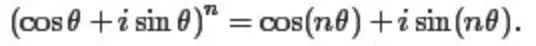
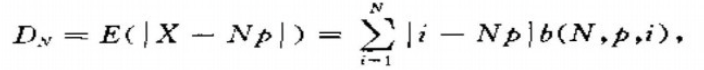
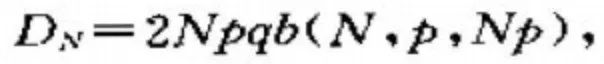
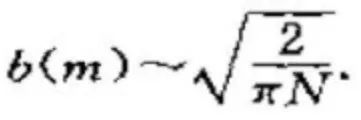
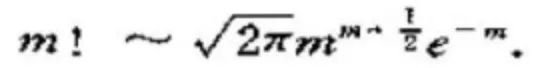 (其中,m=N/2)
(其中,m=N/2)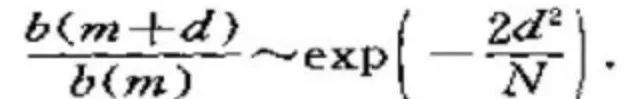
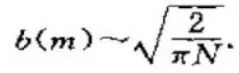 结合后,便有了:
结合后,便有了: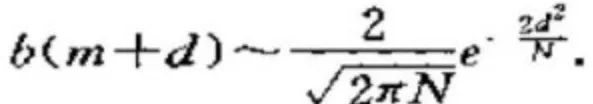
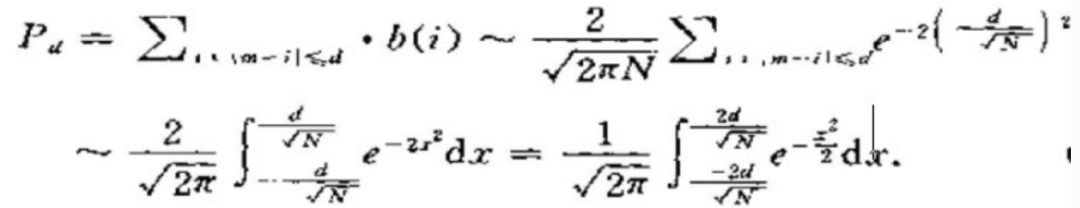
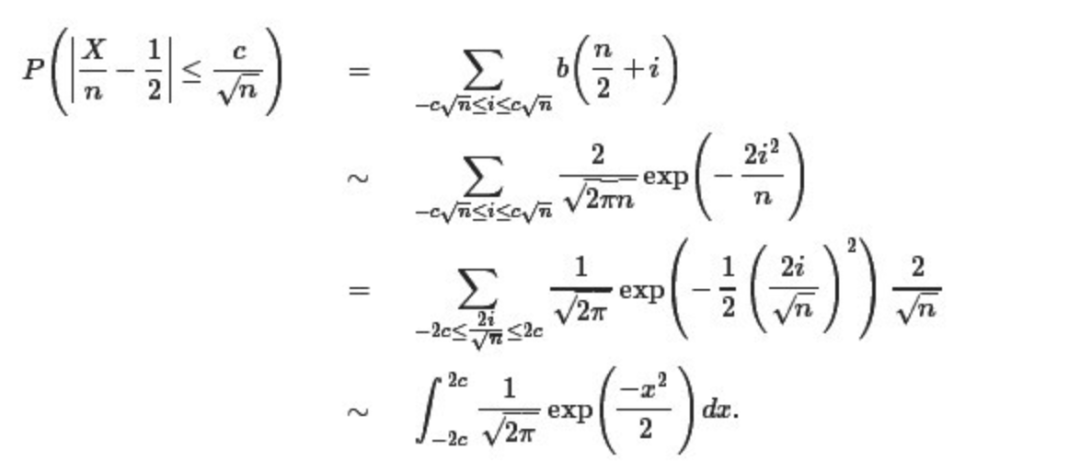
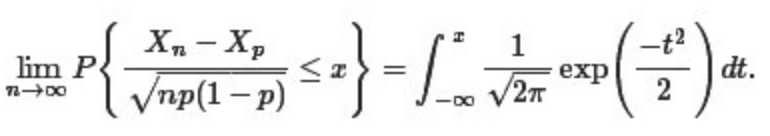
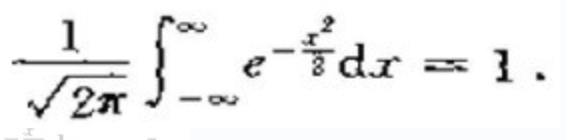
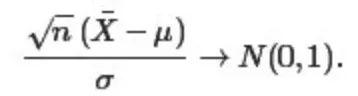
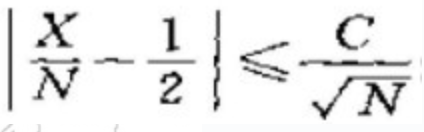 |的概率可任意接近于1,由于
|的概率可任意接近于1,由于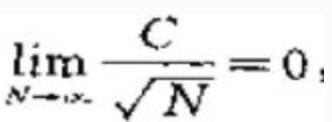 ,故对于任意给定的ε>0,有下式成立:
,故对于任意给定的ε>0,有下式成立: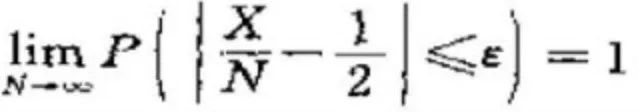

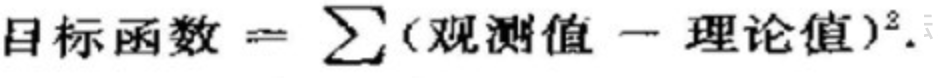
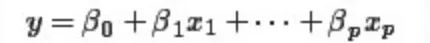
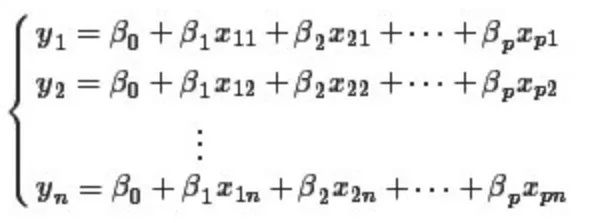
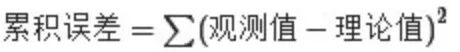
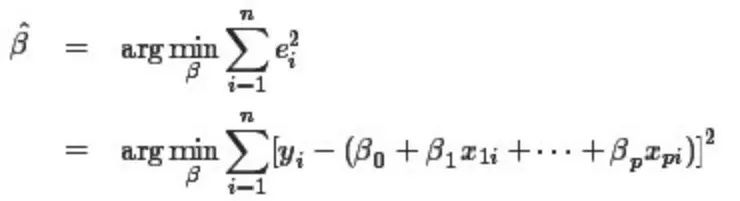
 为n次测量值,现在用测量值
为n次测量值,现在用测量值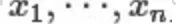 去估计真值θ,那么每次测量的误差为
去估计真值θ,那么每次测量的误差为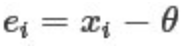 。
。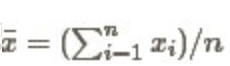 去估计θ呢,则其误差为
去估计θ呢,则其误差为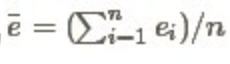 。
。
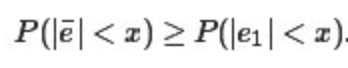
 相比于
相比于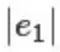 取小值的机会更大。辛普森的这个工作很粗糙,但是这是第一次在一个特定情况下,从概率论的角度严格证明了算术平均的优良性。
取小值的机会更大。辛普森的这个工作很粗糙,但是这是第一次在一个特定情况下,从概率论的角度严格证明了算术平均的优良性。 去估计真值θ。
去估计真值θ。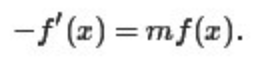
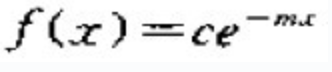 ,C>0且为常数,由于
,C>0且为常数,由于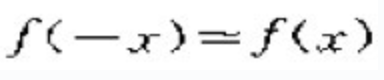 ,得
,得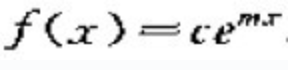 。故当x
。故当x