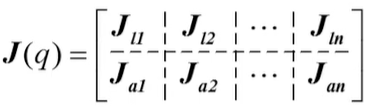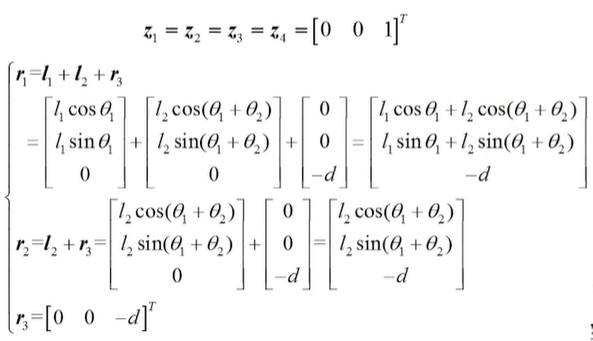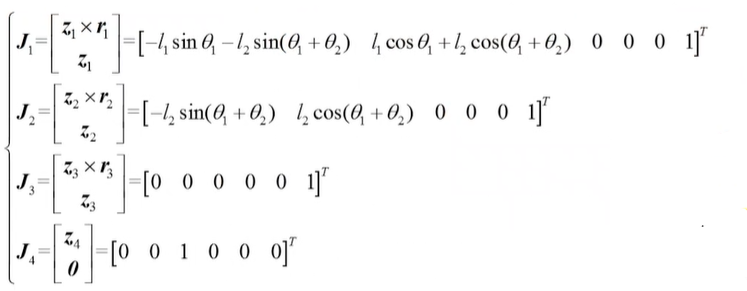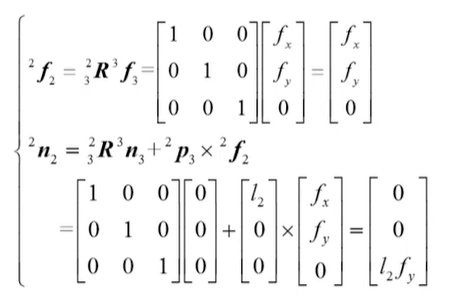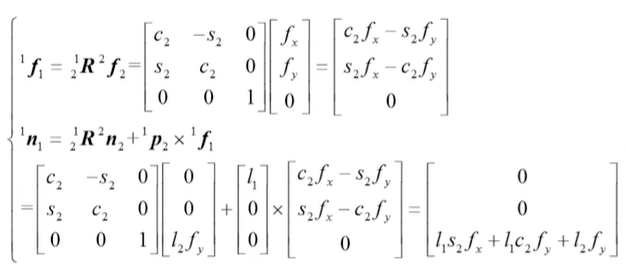机器人操作臂的速度与静力分析

您所在的位置：网站首页 › 机器人的运动速度与摇杆的偏转量成什么 › 机器人操作臂的速度与静力分析

机器人操作臂的速度与静力分析

2024-07-12 16:12:58| 来源: 网络整理| 查看: 265

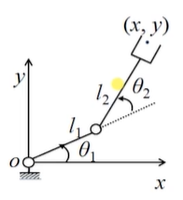
一、速度雅可比的求导法

位置求导法

二、速度雅可比的矢量积法

三、连杆的受力和平衡方程

一、速度雅可比的求导法

机器人是一个多输入多输出的运动系统，为了更好地控制机器人的运动，必须精确求解机器人操作空间与关节空间之间的速度关系。

雅可比矩阵 $J(q)$ 定义为：关节空间速度向末端操作空间速度传递的映射矩阵，可以通过下式来认识雅克比矩阵。

$\dot{\boldsymbol{X}}=\boldsymbol{J}(q) \dot{q}$

求解速度雅克比矩阵的方法有：

位置求导法：运动方程直接求导

矢量积法：矢量方法求解，表达形式简单

微分变换法：相对动坐标系的微分运动

速度递推法：从基座递推各连杆线速度与角速度

位置求导法

机器人的m维操作空间X与n维关节空间q之间的位移关系为

$X=f(q)\Leftrightarrow \left\{\begin{array}{cc} x_{1} & =f_{1}\left(q_{1}, \cdots, q_{n}\right) \\ \vdots & \vdots\\ x_{m}& =f_m\left(q_{1}, \cdots, q_{n}\right) \end{array}\right.$

将两边对时间求导，可得到操作空间的速度与关节速度之间的关系：

$\begin{array}{l} \dot{x}_{1}=\frac{\partial x_{1}}{\partial q_{1}} \dot{q}_{1}+\frac{\partial x_{1}}{\partial q_{2}} \dot{q}_{2}+\cdots \frac{\partial x_{1}}{\partial q_{n}} \dot{q}_{n} \\ \vdots \\ \dot{x}_{m}=\frac{\partial x_{m}}{\partial q_{1}} \dot{q}_{1}+\frac{\partial x_{m}}{\partial q_{2}} \dot{q}_{2}+\cdots \frac{\partial x_{m}}{\partial q_{n}} \dot{q}_{n} \end{array}$

其中 $\dot{x_i},\,i\in(1,m)$ 为末端操作空间的速度， $\dot{q_j},j\in(1,n)$ 为关节空间速度。

求导后的式子可以用矩阵表达为：

$\begin{array}{c} \dot{\boldsymbol{X}}=\boldsymbol{J} \dot{q}, \dot{\boldsymbol{X}}=\left[\begin{array}{c} \dot{x}_{1} \\ \vdots \\ \dot{x}_{m} \end{array}\right], \quad \dot{q}=\left[\begin{array}{c} \dot{q}_{1} \\ \vdots \\ \dot{q}_{n} \end{array}\right] \\ \boldsymbol{J}=\left[\begin{array}{ccc} \frac{\partial x_{1}}{\partial q_{1}} & \cdots & \frac{\partial x_{1}}{\partial q_{n}} \\ \vdots & \cdots & \vdots \\ \frac{\partial x_{m}}{\partial q_{1}} & \cdots & \frac{\partial x_{m}}{\partial q_{n}} \end{array}\right]_{m \times n} \end{array}$

J 为 m x n 形式的雅可比矩阵，其各项均为操作空间的参数对各关节变量的偏导数。

例：平面2R机器人如图所示，求该机器人的雅可比矩阵。

该机器人操作空间和关节空间的分量分别为： $\boldsymbol{X}=\left[\begin{array}{ll} x & y \end{array}\right]^{T}, \boldsymbol{q}=\left[\begin{array}{ll} \theta_{1} & \theta_{2} \end{array}\right]^{T}$

末端位置方程：

$\left\{\begin{array}{c} x=l_{1} \cos \theta_{1}+l_{2} \cos \left(\theta_{1}+\theta_{2}\right) \\ y=l_{1} \sin \theta_{1}+l_{2} \sin \left(\theta_{1}+\theta_{2}\right) \end{array}\right.$

上式两端分别对时间求导可得：

$\left\{\begin{array}{l} \dot{x}=v_{x}=\left[-l_{1} \sin \theta_{1}-l_{2} \sin \left(\theta_{1}+\theta_{2}\right)\right] \dot{\theta}_{1}-\left[l_{2} \sin \left(\theta_{1}+\theta_{2}\right)\right] \dot{\theta}_{2} \\ \dot{y}=v_{y}=\left[l_{1} \cos \theta_{1}+l_{2} \cos \left(\theta_{1}+\theta_{2}\right)\right] \dot{\theta}_{1}+\left[l_{2} \cos \left(\theta_{1}+\theta_{2}\right)\right] \dot{\theta}_{2} \end{array}\right.$

$\dot{\theta_1},\, \dot{\theta_2}$ 前面的各项系数就是我们所求的雅可比矩阵的各项。

将上式写为矩阵形式，便可得到雅可比矩阵：

$\begin{array}{c} \dot{\boldsymbol{X}}=\boldsymbol{J} \dot{\boldsymbol{q}}, \quad \dot{\boldsymbol{X}}=\left[\begin{array}{l} v_{x} \\ v_{y} \end{array}\right], \dot{\boldsymbol{q}}=\left[\begin{array}{l} \dot{\theta}_{1} \\ \dot{\theta}_{2} \end{array}\right] \\ \boldsymbol{J}=\left[\begin{array}{ll} -l_{1} \sin \theta_{1}-l_{2} \sin \left(\theta_{1}+\theta_{2}\right) & -l_{2} \sin \left(\theta_{1}+\theta_{2}\right) \\ l_{1} \cos \theta_{1}+l_{2} \cos \left(\theta_{1}+\theta_{2}\right) & l_{2} \cos \left(\theta_{1}+\theta_{2}\right) \end{array}\right] \end{array}$

令 $J_1,\,J_2$ 为雅可比矩阵的第一列矢量和第二列矢量，上式的速度传递关系可表示为：

$\dot{\boldsymbol{X}}=\boldsymbol{J}_{1} \dot{\theta}_{1}+\boldsymbol{J}_{2} \dot{\theta}_{2}$

其中 $J_1,\,J_2$ 分别表示为单位关节速度在末端位置产生的速度分量的传递比，表明机器人的末端空间速度为机器人各关节速度的线性叠加。

二、速度雅可比的矢量积法

矢量积法的思想为：通过将机器人各关节在末端产生的速度进行叠加得到操作速度。

对于移动关节 i :

末端产生的角速度矢量 $\omega_i:\omega_i=0$

末端产生的线速度矢量 $v_i:v_i=\dot{q_i}z_i$ ，其中 $\dot{q_i}$ 为关节速度值， $z_i$ 为关节单位向量。

将其写为矩阵形式：

$\left[\begin{array}{c} \boldsymbol{v}_{i} \\ \boldsymbol{\omega}_{i} \end{array}\right]=\boldsymbol{J}_{i} \dot{q}_{i}, \boldsymbol{J}_{i}=\left[\begin{array}{c} \boldsymbol{z}_{i} \\ \boldsymbol{0} \end{array}\right]$

$J_i$ 对应移动关节的一列雅克比矩阵。

对于转动关节 i :

末端产生的角速度矢量 $\omega_i:\omega_i=\dot{q_i}z_i$

末端产生的线速度矢量 $v_i:v_i=\dot{q_i}\; z_i\times r_i$

其中 $\dot{q_i}$ 为关节速度值， $z_i$ 为关节单位向量。 $z_i ,r_i$ 均可通过运动学模型求解。

将其写为矩阵形式：

$J_i$ 对应转动关节的一列雅克比矩阵。

由此，我们便得到了雅克比矩阵各列的固定形式：

按照运动副从始端到末端的顺序写出各项，即可构造出机器人的雅克比矩阵：

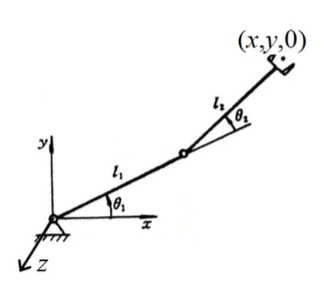
（1）J 的每一列代表相应的关节速度对于末端线速度和角速度的传递比；

（2）前三行代表对末端线速度 v 的传递比；

（3）后三行代表对末端角速度 Ω 的传递比；

例：求平面2R机器人雅可比矩阵（两个运动副都为转动副）

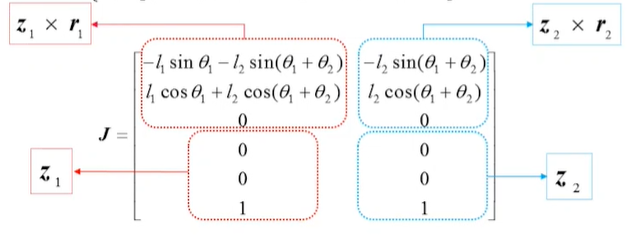
机器人各转轴的单位矢量为：

$z_1=z_2=[0\quad 0\quad 1]^T$

各转轴对应末端点的矢径可根据运动学的关系或矢量叠加的原理得到：

$\{\begin{array}{lll} r_{1}=\left[l_{1} \cos \theta_{1}+l_{2} \cos \left(\theta_{1}+\theta_{2}\right)\right. & l_{1} \sin \theta_{1}+l_{2} \sin \left(\theta_{1}+\theta_{2}\right) & 0]^{T}\\ r_2=[l_{2} \cos \left(\theta_{1}+\theta_{2}\right)&l_{2} \sin\left(\theta_{1}+\theta_{2}\right)&0]^T \end{array}$

然后我们再根据列雅可比矩阵的形式就可写出2R机器人的两列雅可比矩阵，进而得到2R机器人6 x 2形式的雅可比矩阵：

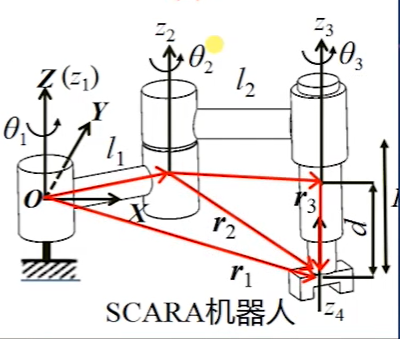
J 表明2R机器人只有xy平面的移动和绕z轴的转动速度。

值得注意的是，此次得到的雅可比矩阵为6 x 2形式，而采用位置求导法得到的雅可比为2 x 2形式，这是因为两种方法使用的操作空间的参数不同。位置求导法以末端（x,y）坐标的速度作为操作空间的参数，而矢量积法将机构末端的六维速度全部表达出。两种方法的结果具有一致性，我们提取矢量积法的前两行，便是位置求导法的结构。

例：求SCARA机器人的雅可比矩阵（前三个关节为转动副，第四关节为移动副）

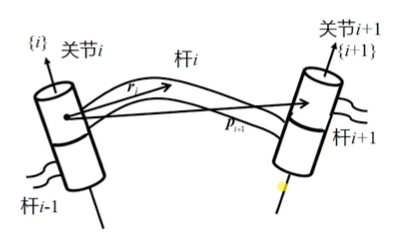
将得到的雅可比矩阵依次排列，就可以到得到SCARA机器人6x4形式的雅可比矩阵：

$J=[J_1\quad J_2\quad J_3\quad J_4]$

三、连杆的受力和平衡方程

机器人的末端操作器通常受到外载荷的作用，各关节的驱动力（矩）通过连杆传递到末端执行器，从而克服外界作用力（矩）。本节研究机器人静止状态下末端操作器所受的外载荷和关节驱动力（矩）之间的关系。即已知末端载荷，求静止状态时的各关节驱动力（矩）。

机器人由连杆和关节组成，以其中一个连杆 i 为对象进行静力分析，连杆 i 以及相邻连杆之间的作用力和作用力矩关系如图所示：

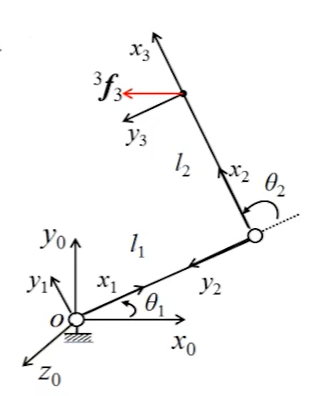
连杆的力和力矩平衡方程在坐标系{i}中表达为：

$\left\{\begin{array}{l} { }^{\prime} \boldsymbol{f}_{i}-{ }^{i} \boldsymbol{f}_{i+1}+{m_{i}}^{i} \boldsymbol{g}=0 \\ { }^{i} \boldsymbol{n}_{i}-{ }^{i} \boldsymbol{n}_{i+1}-{ }^{i} \boldsymbol{p}_{i+1} \times{ }^{i} \boldsymbol{f}_{i+1}+{ }^{i} \boldsymbol{r}_{i} \times m_{i}{ }^{i} \boldsymbol{g}=0 \end{array}\right.$

第一行为连杆 i 的受力平衡方程，第二项为连杆 i 的力矩平衡方程。式中的负号表示连杆 i+1 对连杆 i 的反作用力和反作用矩。矢量左上标 i 表示该矢量在坐标系 i 中的表达； $^i_ir$ 是连杆 i 的质心相对于 i 的表示； $^ip_{i+1}$ 是坐标系{i+1}的原点相对于坐标系{i}的表示。

通常需要根据末端连杆上的载荷，从末端连杆依次递推到操作臂的基座，计算出每个连杆的受力情况。

如果忽略连杆自身的重力，上式可写成反向迭代的形式：

$\left\{\begin{array}{l}^i f_{i}=^if_{i+1} \\ ^in_{i}=^in_{i+1}+^ip_{i+1} \times{ }^{i} f_{i+1} \end{array}\right.$

通过旋转矩阵可将上式有段力（矩）表示在自身坐标系{i+1}中：

$\left\{\begin{array}{l} { }^{i} \boldsymbol{f}_{i}={ }^{i} _{i+1}\boldsymbol{R}^{i+1} \boldsymbol{f}_{i+1} \\ { }^{i} \boldsymbol{n}_{i}={ }_{i+1}^{i} \boldsymbol{R}^{i+1} \boldsymbol{n}_{i+1}+{ }^{i} \boldsymbol{p}_{i+1} \times{ }^{i} \boldsymbol{f}_{i} \end{array}\right.$

该式中的迭代关系非常重要，他可以实现静力从一连杆向另一连杆的传递，根据这一关系可进一步求得各关节的驱动力和力矩。

如果不考虑关节中的摩擦，除了关节驱动力（矩）外，其余各方向的力和力矩分量都由机械构件承受。为了保证连杆平衡，对于转动关节，关节驱动力矩应该等于：

$\tau_{i}={ }^{i} \boldsymbol{n}_{i}{ }^{T} \cdot{ }^{i} \boldsymbol{z}_{i}$

对于移动关节，关节驱动力为：

$\tau_{i}={ }^{i} \boldsymbol{f}_{i}{ }^{T} \cdot{ }^{i} \boldsymbol{z}_{i}$

例：分析平面2R机器人的关节力矩（已知末端受到的平面操作力）。

根据运动学中确定连杆坐标系的方法建立连杆坐标系{0}，{1}，{2}，{3}；

末端操作力在坐标系{3}中表示：

${ }^{3} \boldsymbol{f}_{3}=\left[\begin{array}{c} f_{x} \\ f_{y} \\ 0 \end{array}\right],{ }^{3} \boldsymbol{n}_{3}=\left[\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right]$

我们需要将末端力传递到其他连杆中，求解其他连杆的受力情况。

由连杆坐标系可得相邻连杆旋转变换矩阵：

$^0_1R = \left[ \begin{array} { l l l } { c _ { 1 } } & { - s _ { 1 } } & { 0 } \\ { s _ { 1 } } & { c _ { 1 } } & { 0 } \\ { 0 } & { 0 } & { 1 } \end{array} \right]$ , $^1_2R = \left[ \begin{array} { l l l } { c _ { 2 } } & { - s _ { 2 } } & { 0 } \\ { s _ { 2 } } & { c _ { 2 } } & { 0 } \\ { 0 } & { 0 } & { 1 } \end{array} \right]$ , ${ } _ { 3 } ^ { 2 } R = \left[ \begin{array} { l l l } { 1 } & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 1 } \end{array} \right]$

根据递推公式可得到连杆1对连杆2的作用力和作用力矩：

因此关节2上的驱动力矩为：

$\tau _ { 2 } = { } ^ { 2 } n _ { 2 } ^ { T } \cdot { } ^ { 2 }z_2 = l _ { 2 } f _ { y }$

同理可得到基座对连杆1的作用力和作用力矩：

关节1上的驱动力矩为：

$\tau _ { 1 } = ^1n _ { 1 } ^ { T } \cdot { } _ { 1 }z_1 = l _ { 1 } s _ { 2 } f _ { x } + l _ { 1 } c _ { 2 } f _ { y } + l _ { 2 } f _ { y } + l_2f _ { y }$

将两个关节的关节力矩写成矩阵形式为：

$\left[ \begin{array} { c } { \tau _ { 1 } } \\ { \tau _ { 2 } } \end{array} \right] = \left[ \begin{array} { c c } { l _ { 1 } s _ { 2 } } & { l _ { 1 } c _ { 2 } + l _ { 2 } } \\ { 0 } & { l _ { 2 } } \end{array} \right] \left[ \begin{array} { l } { f _ { x } } \\ { f _ { y } } \end{array} \right]$

将外载荷从坐标系{3}的表示 $^3_3f$ 转换为极坐标系{0}中的表示 $^0_3f$ ：

$^0f _ { 3 } = { } ^0_ { 3 } R\, {}^ { 3 } f _ { 3 } \Rightarrow {}^3f _ { 3 }= { } ^ { 0 } _3R ^ { - 1 } \, ^0 f_3$ ，其中 ${ }^0 _ { 3 } R ^ { - 1 } = \left[ \begin{array} { l l } { C _ { 12 } } & { S _ { 12 } } \\ { - S _ { 12 } } & { C _ { 12 } } \end{array} \right]$

可得：

$\left[ \begin{array} { l } { \tau _ { 1 } } \\ { \tau _ { 2 } } \end{array} \right] = \left[ \begin{array} { c c } { - l _ { 1 } s _ { 1 } - l _ { 2 } s _ { 12 } } & { l _ { 1 } c _ { 1 } + l _ { 2 } c _ { 12 } } \\ { - l _ { 2 } s _ { 12 } } & { l _ { 2 } c _ { 12 } } \end{array} \right] { } ^ { 0 } f _ { 3 }$

式中矩阵即为该机器人的力雅可比矩阵，该矩阵恰巧是上文通过为止求导法求得的速度雅克比矩阵的转置。

【本文地址】

公司简介

联系我们

今日新闻

点击排行

实验室常用的仪器、试剂和: 说到实验室常用到的东西，主要就分为仪器、试剂和耗

不用再找了，全球10大实验: 01、赛默飞世尔科技（热电）Thermo Fisher Scientif

三代水柜的量产巅峰T-72坦: 作者：寞寒最近，西边闹腾挺大，本来小寞以为忙完这

通风柜跟实验室通风系统有: 说到通风柜跟实验室通风，不少人都纠结二者到底是不

集消毒杀菌、烘干收纳为一: 厨房是家里细菌较多的地方，潮湿的环境、没有完全密

实验室设备之全钢实验台如: 全钢实验台是实验室家具中较为重要的家具之一，很多

图片新闻

实验室药品柜的特性有哪些: 实验室药品柜是实验室家具的重要组成部分之一，主要

小学科学实验中有哪些教学: 计算机计算器一般打孔器打气筒仪器车显微镜

实验室各种仪器原理动图讲: 1.紫外分光光谱UV分析原理：吸收紫外光能量，引起分

高中化学常见仪器及实验装: 1、可加热仪器：2、计量仪器：（1）仪器A的名称：量

微生物操作主要设备和器具: 今天盘点一下微生物操作主要设备和器具，别嫌我啰嗦

浅谈通风柜使用基本常识: 　众所周知，通风柜功能中最主要的就是排气功能。在

机器人操作臂的速度与静力分析

机器人操作臂的速度与静力分析

今日新闻

点击排行

推荐新闻

图片新闻

专题文章