多层线性模型HLM相关的文章(嵌套数据的处理) |
您所在的位置:网站首页 › 嵌套模型意义 › 多层线性模型HLM相关的文章(嵌套数据的处理) |
多层线性模型HLM相关的文章(嵌套数据的处理)
|
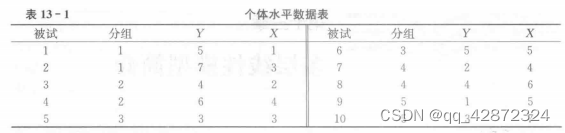
多层线性模型简介 第一节多层线性模型概述 一、多层线性模型分析数据的特点 在社会科学研究中,调查得来的数据往往具有层次结构(嵌套结构)的特点,在心理学研究中这种情况尤为常见,如关于学业成绩影响因素的研究中,我们可以考虑的预测变量有学生的入学成绩、学生性别、学生的社会经济地位、班级人数、班主任和任课教师、教室环境等,这些变量中有的是学生个体变量,有的是班级整体变量。这样的数据具有两个水平,第一水平是学生,第二水平是班级,学生嵌套于班级之中,称为分层数据。如果观测涉及不同的学校• 同时考虑不同的学校变量,则构成一个三水平模型,即学生水平嵌套于班级水平,班级水平嵌套于学校水平。在层次结构数据中,不仅有描述个体的变量,而且有由个体组成的更高一层的变量。在经济学、地理学、心理学和社会学的研究中,不乏这样的数据存在。根据层次结构数据的特点,重复测量的数据也可以看成是具有层次结构的数据,其第一水平为不同测量,第二水平为个体,重复测量数据的这一层次性的特点扩大了多层线性模型的使用范围。 传统的线性回归模型假设变量间存在线性关系,变量总体上服从正态分布,方差齐性,个体间随机误差相互独立。而对于多层数据,传统的回归分析有以下两种处理方法。 (1 ) 在个体(如学生)水平上分析。即将所有的更高一层的变量(即组变量) 都看作第一水平的变量,直接在个体水平上对数据进行分析。这种分析方法存在的问题是,组变量对同一组内的个体有相同的影响,例如,班级变量对同一个班级内的学生有相同的影响,不同班级学生对应不同的班级变量,而不区分班级对学生的影响,假设同一班级的学生间相互独立是不合理的,同样对不同班级的学生和相同班级的学生作同一假设也是不合理的。 为了便于理解和计算,我们举一个简单的例子(例子数据为模拟生成的,实际数据将会更加复杂),以下一组数据中,共有 5 个组,每组 2 名被试,如表 13 - 1 所示。
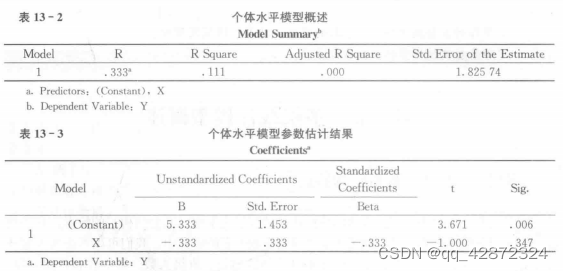
如果忽略组变量,直接在被试个体层面采用预测变量 X 对因变量 Y 进行回归分析,结果如表 13 - 2 和表 13 - 3 所示,
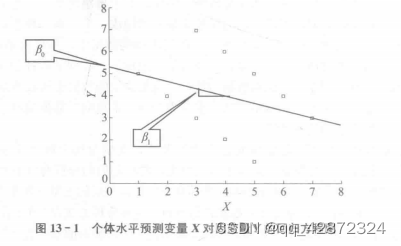
回归方程为:Y=5.333-0.333 X+£。回归方程图如图 13 - 1 所示。
(2) 在组(如班级) 水平上分析。将第一水平的变量直接合并为第二水平的变量,然后直接对组水平(如班级) 做分析,这种分析方法存在的问题是丢失了组内个体间的差异的信息,而在实际中,这一部分的变异往往占总变异中很大的一部分。 如果使用上述案例,将数据合并到组层面,则如表 13 - 4 所示。
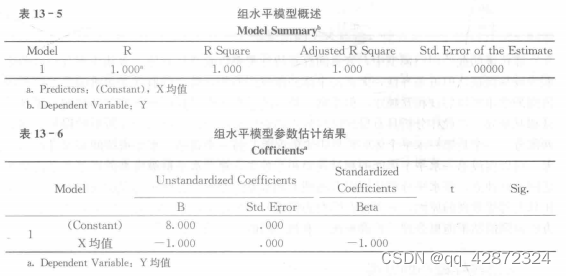
直接在组层面采用预测变量 X 对因变量 y 进行回归分析,结果如表 13 - 5 和表 13 - 6所示。
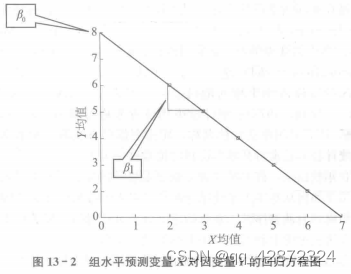
回归方程为:Y—8.000—1.000 X+e。 回归方程图如图 13 - 2 所示。
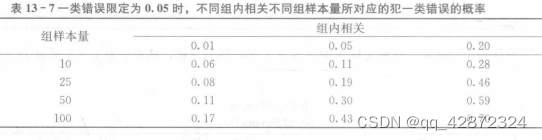
上述两种方法有可能得到不同的结果,在对结果的解释上也很不一致。基于上述的讨论,这两种分析数据的方法有一个共同点,即它们都没有考虑数据间分层的特点,有可能对数据结果做出不合理的甚至是错误的解释。这就是传统回归分析方法在分析具有结构层次特点数据时的局限性。具体来讲,传统回归分析没有考虑同一组观测值之间误差的相关,得到的标准误往往偏小,犯一类错误的概率往往偏大。如表 13 - 7 所示,已有研究发现,当组内相关为 0.20,一类错误率限定为 0.05, 且组内样本量达到 100 时,实际所犯—类错误的概率高达 0.70 (Barcikowski,1981;Kreft de Leeuw, 1998)。
在传统的线性回归模型中,变量间存在线性关系以及变量总体上服从正态分布这两个假设较易保证,但方差齐性,尤其是个体间随机误差相互独立的假设却很难满足。即不同班级的学生可以假设相互独立,但是同一班级的学生由于受相同班级变量的影响,很难保证相互独立。因此在分析具有层次结构特点的数据时,应将传统回归分析中的误差分解为两部分,一个是第一水平个体间差异带来的误差,另一个是第二水平班级间差异带来的误差。可以假设第一水平个体间的测量误差相互独立,第二水平班级带来的误差在不同班级之间相互独立。多水平分析法同时考虑到不同水平的变异,这也正是多层线性分析法的应用越来越受重视的原因,它不仅在模型的假设上与实际情况更加吻合,更重要的是由这种方法得到的结果能更合理、正确地揭示事物之间的真正关系。 二、多层线性模型的发展 多层线性模型在不同的学科领域有不同的名称,如在社会学的研究中常用多水平线性模型(multilevel linear model ) 这 一 术 语 (例 如,Goldstein, 1987;Mason,Wong,& - Entwisle,1983);在生物计量学中,常采用混合效应模型 (mixed-effects model) 或 随 机效 应 模 型 ( random-effect model) 这 一 术 语 (例 如,Elston & Grizzle,1962;Laird 8/. Ware, 1982);在计量经济学中称为随机系数回归模型(mndom-coefficiem model; 例 如,Rosenberg,1973);统计学中用协方差成分模型 ( covariance components model) 这一术语。不管采用什么样的名称,实质上都没有区别。在本书中,我们采用能够充分体现这一统计技术数据特征的多层线性模型这一术语。 自 20 世纪 70 年代以来,许多研究者开始寻求怎样将系统的方法引入社会科学的研究中,主要是一种关于如何从整体上系统地分析研究得来的数据特征和合理建立模型的统计方法。协方差结构模型为从整体的、系统的角度分析事物间的因果关系提供了可能,使得传统回归分析的方法从理论上和实际应用上都得到了相当范围的推广。自 20 世纪 80 年代以来,Aitkin 和 Longford (1986) 等将系统的方法应用于具有层次特征结构数据的统计建模和分析中,这一方法的主要原理就是多层线性模型的理论。20 世纪 90 年代初期,随着计算机技术的发展,出现了专门用于分析具有多层特征结构数据的软件。从多层分析法的发展阶段来看,主要经历了以下三个阶段。 (一)模型理论构想阶段 多层线性模型这一术语最早由 Lindley 和 Smith 于 1972 年提出,这一模型的提出对后来贝叶斯线性模型的发展起到很大的作用,他们构建了具有复杂误差结构的嵌套数据的一般模型结构。但是由于该模型参数估计的方法与传统的回归方法不同,他们提岀的模型需要估计非平衡数据的方差成分和不同水平的误差协方差矩阵,在计算上遇到了很大的障碍,正是由于计算技术的限制,它在很长一段时间内没得到推广。这一阶段发展的主要特点是仅限于理论上对该模型进行探讨。 (二)问题解决阶段 Dempster,Laird 和 Rubin (1977) 等提出的 EM 算法,使得解决参数估计这一问题有了实质性的突破。Dempster,Rubin 和 Tsutakawa (1981) 等将 EM 算法应用于解决多层线性模型的参数估计,使这一方法的应用成为可能。Strenio,Weisberg 和 Bryk (1983) 等相继将这一方法应用于社会学的研究,使这一方法得以具体应用。随后,Goldstein (1986) 应用迭代加权广义最小二乘法 (iteratively reweightecl generalized least squares)估计参数,Longford (1987) 应用 Fisher 得分算法 (Fisher scoring algorithm) 对模型参数进行了估计。在这一阶段,发展出了一系列估计参数的理论和计算方法。 (三)快速发展阶段 随着参数估计问题的解决和计算机技术的发展,很多算法被程序化,相继出现了一些相应的软件,目前较常用的有 HLM、 Mplus, SPSS、MlwiN 和 VARCL 等。这一系列统计软件的开发和应用使这一方法很快被应用于社会科学各个领域的研究。 三、多层线性模型在心理学研究中的应用 正如前面所述,心理学研究中得来的大量资料都具有层次结构的特点,数据间复杂的结构关系,使得传统线性回归方法的假设难以满足。多层线性模型的提出为正确解决这一问题提供了可能,它不仅从方法上考虑复杂的变量误差之间的关系,还能更加合理地从理论上解释变量之间的关系。用多层线性模型分析具有嵌套结构的数据主要出于以下几方面的考虑:(1) 多层线性模型能更加合理地估计个体变量对于因变量的影响;(2) 多层线性模型可以考虑不是同一水平的变量间的影响,如可以考虑班级人数对于学生学业成绩的影响;(3) 多层线性模型可以在多水平间分解方差和协方差成分,如可以将一组学生水平变量之间的相关分解为学校内和学校间两个部分。 多层线性模型在处理心理学研究中具有层次结构特点的数据时,与传统方法相比有以下几方面的优点。 (1) 多层线性模型由于建立在更合理的假设之上,考虑了不同层次的随机误差和变量信息.能提供正确的标准误估计,从而得到更有效的区间估计和更精确的假设检验。 (2) 多层线性模型可以分析计算任何水平上测量的协方差,使得研究者可以探讨诸如班级和学生的其他特征对因变量的差异到底起多大的作用这样的问题。如可以通过计算不同水平变异在总变异中所占的比例来确定不同水平对因变量的影响程度。 (3) 使用多层线性分析的方法可以发现所得到的回归方程中的截距和斜率之间的相关关系,从而能更好地解释预测变量与因变量间变化的规律。 (4 ) 多层线性分析不仅可以用于分析观测变量之间的因果关系,而且作为协方差结构模型的拓展,可以分析具有多层结构的潜变量之间的因果关系,即建立多水平结构方程模型。 (5) 多层线性分析不仅可以用来分析具有层次结构的数据,而且可以分析重复测量的数据,在此情况下,可以将测量看作第一水平,将测试个体看作第二水平。 (6) 多层线性分析模型不仅可以对服从正态分布的连续型测量数据进行分析. 而且可以分析离散型的数据资料,如服从二项分布和泊松分布的数据等。 另外,多层线性模型在心理学研究中,使用范围较广,许多传统统计方法都是它的特例。如假设在两水平模型中有一个水平的变量为常数,则多层线性分析就可简化为传统的回归分析;此外,单因素方差分析、单因素协方差分析也可以看成是多层分析的简化。 在心理学中应用层次分析的方法,可以对许多问题产生新的更重要的洞察与理解,可以更加合理地解释某些心理现象。但是作为一种统计分析的方法,和以往任何一种方法一样,它并不能解决所有的问题,如果数据不具有结构性,则不必要用层次分析法,用传统的单水平模型分析就可以得到很好的解释。另外,虽然用多层分析可以更准确地描述事物之间的因果关系,但这一方法并不能用来建立理论,不能代替专业理论方面的分析。 第二节多层线性分析主要回答的问题 传统的多元回归分析可以回答以下问题:(1 ) 预测变量和因变量的关系,例如,学生学业成绩是否和学生的学习动机和教师教学热情存在相关;(2) 预测变量的重要性程度,例如,学生的学习动机和教师教学热情的重要性程度如何;(3) 模型中加入其他变量后,预测变量对因变量的影响是否会发生变化,例如,研究者们常常在模型中加入控制变量学校平均社会经济地位,分析学生学业成绩是否和学生的学习动机和教师教学热情存在相关;(4) 预测变量之间的交互作用,例如不同学生学习动机对学生学业成绩的影响是否会受到不同水平的教师教学热情的影响;(5) 参数估计结果,例如,预测变量学生学习动机的斜率;(6) 在新样本中预测因变量。多层线性模型与传统回归模型相似,均可以回答传统回归模型中的所有问题。例如,预测变量的重要性程度是所有回归模型均需要回答的问题。在多层线性模型中,这一问题即第一水平个体的预测变量和第二水平小组的预测变量 对因变量影响的重要性程度。比如:第一种方法为对学生水平的学习动机进行干预,第二种方法为对班级水平的教师教学热情进行干预,哪种方法对学生学业成绩的提高效果更佳?除此之外. 多层线性模型主要还可以对以下内容进行详细阐述。 一、组间均值差异 组间均值差异是多层线性分析中第一步需要回答的问题,也就是说组间是否存在显著的截距(均值) 差异。例如,不同班级之间学生的学业成绩是否存在显著差异。 二、组间斜率差异 组间斜率差异也是多层线性分析过程中可以回答的问题,也就是说组间是否存在显著的斜率差异。例如,不同班级之间学生动机对学生学业成绩的影响是否存在显著差异,或者不同班级之间教师教学热情对学生学业成绩的影响是否存在显著差异。 三、跨级交互作用 跨级交互作用是指第一水平个体的预测变量与第二水平小组的预测变量是否存在交互作用。例如,学校平均社会经济地位(第三水平的变量) 和学生的学习动机(第一水平的变量) 对学生的学业成绩的影响是否存在交互作用,或者教师教学热情 (第二水平的变量) 和学生的学习动机(第一水平的变量)对学生的学业成绩的影响是否存在交互作用。 四、对追踪数据的分析 多层线性模型的发展为追踪(个体变化)研究提供了一个强大的方法体系。许多个体变化现象可以通过一个两水平线性模型来解释。对个体的多次观察嵌套于个体之中。多层线性模型分析结果可以回答:(1) 个体的变化趋势,如学生因变量是否呈线性增长趋势?(2) 个体的变化趋势是否存在个体差异?(3) 个体的变化趋势受哪些因素影响? 五、元分析 元分析是用来整合以及描述大量独立研究的定量研究方法,它是对统计结果的再统计。研究材料包含来自许多具有相同研究主题的不同研究,如果同时将其归类,则具有典型的嵌套结构,即独立研究嵌套于相应类别。例如,研究者有 100 多个有关学生学业成绩的研究结果,通过每个研究的研究结果可以获得平均值、标准差、P 值、效应值等指标。如果将数据建构为多层数据,独立研究则为多层线性模型的第一水平。元分析可以回答: (1) 不同研究的效应值是否存在显著差异?(2) 预测变量(例如学生学习动机、教师的教学热情等) 是否对研究的效应值有显著影响?(3) 预测变量(例如学生学习动机、教师的教学热情等)是否对不同类别研究的差异有显著影响? 第三节多层线性分析中的模型及假设 本节主要介绍两水平的数学模型及其常用的模型类型。通过参数间关系可以看出,传统统计中常用的线性回归分析、方差分析、协方差分析等方法都可以被看作多层线性模型在一些限定条件下的特例。此外,本节还将介绍常用的一些数据转换的方法及在结果解释时应该注意的问题。 我们从一个简单的例子入手来看一下,传统回归分析方法在分析具有层次结构的数据时存在的问题。 对 73 所学校 1 905 名学生进行调查,目的是考察其刚上高中时的入学成绩与三年后高考成绩之间的关系。可以从以下几方面考虑:(1) 用传统的线性回归分析,直接在学生水平上进行分析,得出入学学业成绩对高考成绩的一条回归直线,如图 13- 3 所示,从图中结果可以看岀,传统回归分析没有区分不同的学校之间的差异。(2) 将数据进行简单合并,用每个学校学生的平均成绩代替这个学校的成缋,直接在学校水平上估计入学成绩对高考成绩的影响,得到一条回归直线,如图 13- 4 所示,这种方法忽略了不同学生之间的差异。(3) 假设不同学校入学成绩对高考成绩的回归直线截距不同,斜率相同(平均学习成绩之间存在差异),得到如图 13 - 5 的结果,从图中结果可以看出,不同学校学生平均高考成绩之间存在差异。(4) 对 73 所学校分别做回归分析,得到如图 13 - 6 的结果• 可以看出,不同学校回归直线的截距和斜率均不同,即不同学校学生平均高考成绩之间存在差异,入学成绩对高考成绩的影响强度不同。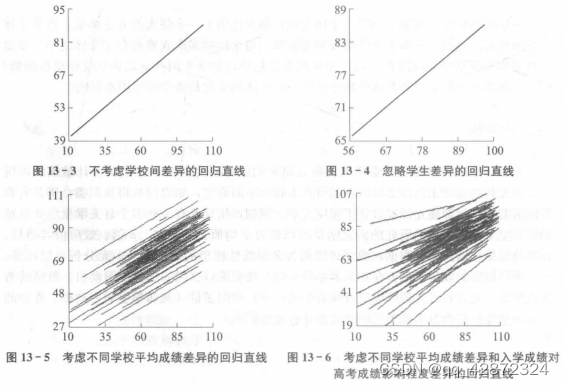 从以上的分析过程可以看出,传统的回归分析方法将数据合并,直接在第二个水平上对变量之间的关系进行分析,或不考虑第二水平对数据之间关系的影响直接对数据进行分析都是不合理的,有时可能会得到错误的结论。多层分析是多元回归分析的自然延伸,主要用来处理具有嵌套关系的数据,预测变量与因变量之间的关系。与回归分析的主要区別在于多层分析法是在更加合理的假设基础上的一种分析方法,对数据结果的解释更有意义,也更接近实际。下面首先介绍最简单的两水平线性分析模型。
一、两水平线性分析的数学模型
我们首先从只有一个学校的学生人学成绩对高考成绩的影响的回归分析人手,以逐步揭示多层分析法的实质。对于一个学校来说,要考察两个变量之间的关系,用传统回归分析的方法,可建立如下的回归方程:
从以上的分析过程可以看出,传统的回归分析方法将数据合并,直接在第二个水平上对变量之间的关系进行分析,或不考虑第二水平对数据之间关系的影响直接对数据进行分析都是不合理的,有时可能会得到错误的结论。多层分析是多元回归分析的自然延伸,主要用来处理具有嵌套关系的数据,预测变量与因变量之间的关系。与回归分析的主要区別在于多层分析法是在更加合理的假设基础上的一种分析方法,对数据结果的解释更有意义,也更接近实际。下面首先介绍最简单的两水平线性分析模型。
一、两水平线性分析的数学模型
我们首先从只有一个学校的学生人学成绩对高考成绩的影响的回归分析人手,以逐步揭示多层分析法的实质。对于一个学校来说,要考察两个变量之间的关系,用传统回归分析的方法,可建立如下的回归方程:
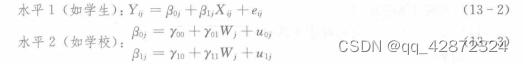 合并的模型可表示为:
合并的模型可表示为:


 二、多水平分析常用的简化模型类型
多水平分析模型作为处理变量之间关系的一种统计分析方法,与回归分析类似,可以处理类似于方差分析和协方差分析的问题,同时回归分析也可以作为多水平分析模型的特例。下面主要在公式(13 - 2) 和公式(13 - 3) 所定义的只含一个第一水平变量和一个第二水平变量的简单层次分析模型的基础上,简要介绍几种常用的简化模型。
(一)随机效应一元方差分析模型
二、多水平分析常用的简化模型类型
多水平分析模型作为处理变量之间关系的一种统计分析方法,与回归分析类似,可以处理类似于方差分析和协方差分析的问题,同时回归分析也可以作为多水平分析模型的特例。下面主要在公式(13 - 2) 和公式(13 - 3) 所定义的只含一个第一水平变量和一个第二水平变量的简单层次分析模型的基础上,简要介绍几种常用的简化模型。
(一)随机效应一元方差分析模型

 (二)随机效应单因素协方差分析模型
(二)随机效应单因素协方差分析模型
 (三)一般的线性回归模型
(三)一般的线性回归模型
 (四)随机系数回归模型
(四)随机系数回归模型
 三、多层线性模型中的参数估计
三、多层线性模型中的参数估计
|
【本文地址】
今日新闻 |
点击排行 |
|
推荐新闻 |
图片新闻 |
|
专题文章 |